Введем теперь очень важную термодинамическую характеристику, называемую теплоемкостью системы (традиционно обозначается буквой С с различными индексами).
Теплоемкость системы — это физическая величина, равная количеству теплоты, которое необходимо передать системе, чтобы увеличить ее температуру на один кельвин (градус):
|
Теплоемкость — величина аддитивная, она зависит от количества вещества в системе. Поэтому вводят также удельную теплоемкость
Удельная теплоемкость — это теплоемкость единицы массы вещества
|
и молярную теплоемкость
Молярная теплоемкость — это теплоемкость одного моля вещества
|
Поскольку количество теплоты не есть функция состояния и зависит от процесса, теплоемкость также будет зависеть от способа подвода тепла к системе. Чтобы понять это, вспомним первое начало термодинамики.
Разделив равенство (2.4) на элементарное приращение абсолютной температуры dT, получим соотношение
| (2.18) |
Второе слагаемое, как мы убедились, зависит от вида процесса. Отметим, что в общем случае неидеальной системы, взаимодействием частиц которой (молекул, атомов, ионов и т. п.) пренебречь нельзя (см., например, § 2.5 ниже, в котором рассматривается ван–дер–ваальсовский газ), внутренняя энергия зависит не только от температуры, но и от объема системы.
Это объясняется тем, что энергия взаимодействия зависит от расстояния между взаимодействующими частицами. При изменении объема системы меняется концентрация частиц, соответственно, меняется среднее расстояние между ними и, как следствие, меняется энергия взаимодействия и вся внутренняя энергия системы.
Другими словами, в общем случае неидеальной системы
.
Поэтому, в общем случае первое слагаемое нельзя писать в виде полной производной, полную производную необходимо заменить на частную производную с дополнительным указанием на то, при какой постоянной величине она вычисляется. Например, для изохорного процесса:
Или для изобарного процесса
- Входящая в это выражение частная производная вычисляется с помощью уравнения состояния системы, записанного в виде . Например, в частном случае идеального газа
- ,
- эта производная равна
Мы рассмотрим два частных случая, соответствующих процессу подведения теплоты:
- постоянном объеме;
- постоянном давлении в системе.
В первом случае работа dА = 0 и мы получаем теплоемкость СV идеального газа при постоянном объеме:
| (2.19) |
- С учетом сделанной выше оговорки, для неидеальной системы соотношение (2.19) необходимо записать в следующем общем виде
- Заменив в 2.7 на , а на немедленно получаем:
Для вычисления теплоемкости идеального газа Сp при постоянном давлении (dp = 0) мы учтем, что из уравнения (2.8) следует выражение для элементарной работы при бесконечно малом изменении температуры
Получаем в итоге
| (2.20) |
Разделив это уравнение на число молей вещества в системе, получаем аналогичное соотношение для молярных теплоемкостей при постоянном объеме и давлении, называемое соотношением Майера
| (2.21) |
Приведем для справки общую формулу — для произвольной системы — связывающую изохорную и изобарную теплоемкости:
Выражения (2.20) и (2.21) получаются из этой формулы путем подстановки в неё выражения для внутренней энергии идеального газа и использования его уравнения состояния (см. выше):
.
Теплоемкость данной массы вещества при постоянном давлении больше теплоемкости при постоянном объеме, так как часть подведенной энергии тратится на совершение работы и для такого же нагревания требуется подвести больше теплоты. Отметим, что из (2.21) следует физический смысл газовой постоянной:
| Газовая постоянная R — это работа, совершаемая молем идеального газа при повышении его температуры на 1 К при постоянном давлении. |
Таким образом, теплоемкость оказывается зависящей не только от рода вещества, но и от условий, в которых происходит процесс изменения температуры.
Как мы видим, изохорная и изобарная теплоемкости идеального газа от температуры газа не зависят, для реальных веществ эти теплоемкости зависят, вообще говоря, также и от самой температуры Т.
Изохорную и изобарную теплоемкости идеального газа можно получить и непосредственно из общего определения, если воспользоваться полученными выше формулами (2.7) и (2.10) для количества теплоты, получаемого идеальным газом при указанных процессах.
Для изохорного процесса выражение для СV следует из (2.7):
| (2.22) |
Для изобарного процесса выражение для Ср вытекает из (2.10):
| (2.23) |
Для молярных теплоемкостей отсюда получаются следующие выражения
| (2.24) |
Отношение теплоемкостей равно показателю адиабаты:
На термодинамическом уровне нельзя предсказать численное значение g; нам удалось это сделать лишь при рассмотрении микроскопических свойств системы (см. выражение (1.19), а также (1.28) для смеси газов). Из формул (1.19) и (2.24) следуют теоретические предсказания для молярных теплоемкостей газов и показателя адиабаты.
Одноатомные газы (i = 3):
| (2.25) |
Двухатомные газы (i = 5):
| (2.26) |
Многоатомные газы (i = 6):
| (2.27) |
Экспериментальные данные для различных веществ приведены в таблице 1.
Таблица 1
| Вещество | g | ||
| He Ar | 20,97 20,79 | 12,65 12,43 | 1,66 1,67 |
|
|
|
|
| CO2 NH3 | 37,23 36,70 | 28,74 27,73 | 1,30 1,32 |
|
|
|
|
Видно, что простая модель идеальных газов в целом неплохо описывает свойства реальных газов. Обращаем внимание, что совпадение было получено без учета колебательных степеней свободы молекул газа.
Мы привели также значения молярной теплоемкости некоторых металлов при комнатной температуре.
Если представить кристаллическую решетку металла как упорядоченный набор твердых шариков, соединенных пружинками с соседними шариками, то каждая частица может только колебаться в трех направлениях (iкол = 3), и с каждой такой степенью свободы связаны кинетическая kВТ/2 и такая же потенциальная энергия. Поэтому на частицу кристалла приходится внутренняя (колебательная) энергия kВТ. Умножая на число Авогадро, получим внутреннюю энергию одного моля
- откуда вытекает значение молярной теплоемкости
- (Вследствие малого коэффициента теплового расширения твердых тел для них не различают ср и cv). Приведенное соотношение для молярной теплоемкости твердых тел называется законом Дюлонга и Пти, и из таблицы видно хорошее совпадение расчетного значения
- с экспериментом.
Говоря о неплохом соответствии приведенных соотношений и данных опытов, следует отметить, что оно наблюдается лишь в определенном диапазоне температур.
Иначе говоря, теплоемкость системы зависит от температуры, и формулы (2.24) имеют ограниченную область применения. Рассмотрим сначала рис. 2.
10, на котором изображена экспериментальная зависимость теплоемкости стV газообразного водорода от абсолютной температуры Т.
Рис. 2.10. Молярная теплоемкость газообразного водорода Н2 при постоям ном объеме как функция температуры (экспериментальные данные)
Ниже, для краткости, говорится об отсутствии у молекул тех или иных степеней свободы в определенных температурных интервалах. Еще раз напомним, что речь в действительности идет о следующем.
По квантовым причинам, относительный вклад во внутреннюю энергию газа отдельных видов движения действительно зависит от температуры и в определенных температурных интервалах может быть мал настолько, что в эксперименте — всегда выполняемом с конечной точностью — он незаметен.
Результат эксперимента выглядит так, как будто этих видов движения нет, нет и соответствующих степеней свободы. Число и характер степеней свободы определяются структурой молекулы и трехмерностью нашего пространства — от температуры они зависеть не могут.
- Вклад во внутреннюю энергию от температуры зависит и может быть мал.
- При температурах ниже 100 К теплоемкость
- что указывает на отсутствие у молекулы как вращательных, так и колебательных степеней свободы. Далее с ростом температуры теплоемкость быстро возрастает до классического значения
- характерного для двухатомной молекулы с жесткой связью, в которой нет колебательных степеней свободы. При температурах свыше 2 000 К теплоемкость обнаруживает новый скачок до значения
Этот результат свидетельствует о появлении еще и колебательных степеней свободы. Но все это пока выглядит необъяснимым.
Почему молекула не может вращаться при низких температурах? И почему колебания в молекуле возникают лишь при очень высоких температурах? В предыдущей главе дано краткое качественное рассмотрение квантовых причин подобного поведения.
А сейчас можно лишь повторить, что все дело сводится к специфически квантовым явлениям, не объяснимым с позиций классической физики. Эти явления подробно рассмотрены в последующих разделах курса.
Дополнительная информация
http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 236 — таблица характеристических температур «включения» колебательных и вращательных степеней свободы молекул для некоторых конкретных газов;
Обратимся теперь к рис. 2.11, представляющему зависимость молярных теплоемкостей трех химических элементов (кристаллов) от температуры. При высоких температурах все три кривые стремятся к одному и тому же значению
соответствующему закону Дюлонга и Пти. Свинец (Рb) и железо (Fe) практически имеют это предельное значение теплоемкости уже при комнатной температуре.
Рис. 2.11. Зависимость молярной теплоемкости для трех химических элементов — кристаллов свинца, железа и углерода (алмаза) — от температуры
Для алмаза же (С) такая температура еще не достаточно высока. А при низких температурах все три кривые демонстрируют значительное отклонение от закона Дюлонга и Пти. Это еще одно проявление квантовых свойств материи. Классическая физика оказывается бессильной объяснить многие наблюдаемые при низких температурах закономерности.
Дополнительная информация
http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 106–107, ч. I, § 12 — вклад электронов в теплоемкость металлов при температурах близких к абсолютному нулю;
http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_82.htm — Перельман Я.И. Знаете ли вы физику? Библиотечка «Квант», выпуск 82, Наука,1992г. Стр. 132, вопрос 137: какие тела обладают наибольшей теплоемкостью (ответ смотри на стр. 151);
http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_82.htm — Перельман Я.И. Знаете ли вы физику? Библиотечка «Квант», выпуск 82, Наука,1992г. Стр. 132, вопрос 135: о нагревании воды в трех состояниях — твердом, жидком и парообразном (ответ смотри на стр. 151);
http://www.femto.com.ua/articles/part_1/1478.html — физическая энциклопедия. Калориметрия. Описаны методы измерения теплоемкостей.
ТЕПЛОЕМКОСТЬ


 А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
ТЕПЛОЕМКОСТЬ, кол-во теплоты, затрачиваемое для изменения т-ры на 1 °С. Согласно более строгому определению, теплоемкость-термодинамич. величина, определяемая выражением:
где DQ- кол-во теплоты, сообщенное системе и вызвавшее изменение ее т-ры на DТ. Отношение конечных разностей DQ/DТ наз. средней теплоемкостью, отношение бесконечно малых величин dQ/dT-истинной теплоемкостью.
Поскольку dQ не является полным дифференциалом ф-ции состояния, то и теплоемкость зависит от пути перехода между двумя состояниями системы. Различают теплоемкость системы в целом (Дж/К), удельную теплоемкость [Дж/(г·К)], молярную теплоемкость [Дж/(моль·К)].
Во всех ниже приведенных ф-лах использованы молярные величины теплоемкости.
Из второго начала термодинамики следует, что теплоемкость пропорциональна производной от энтропии системы S по т-ре Т при постоянстве внеш. силы или термодинамич. координаты (обозначается индексом z):
- Наиб. важными видами теплоемкости являются теплоемкость CV при постоянном объеме V и теплоемкость Ср при постоянном давлении р:
- СV = (9U/9T)V = T(9S/9T)V, Ср = (9Н/9Т)р = Т(9S/9Т)р,
где U-внутр. энергия, H-энтальпия системы. Значения Ср и СV связаны соотношением:
где a = V-1(9V/9Т)р-коэф. термич. расширения, x = = — V-1(9V/9р)T-коэф. изотермич. сжимаемости. Поскольку по условиям устойчивости фаз Ср, CV > 0 и (9V/9р)T < 0, то согласно (3) Ср > CV. Это естественно, т. к. при изобарич.
нагревании часть тепла, помимо увеличения внутр. энергии системы, идет на работу расширения. Для идеальных газов (9U/9V)T = 0 и учет ур-ния состояния pV= RT приводит к соотношению: Сp — CV = R (R-газовая постоянная). Из определений (1) и (2) следует, что для изотермич.
процесса С = ,, для адиабатич. процесса С = 0.
Теплоемкость газов. Вычисление теплоемкости сводится к вычислению средней энергии теплового движения отдельных молекул, к-рое складывается из поступат. и вращат. движений молекулы как целого и из колебаний атомов внутри молекулы.
Молярная теплоемкость одноатомного газа равна 3R/2 (по R/2 на каждую степень поступат. движения молекулы). теплоемкость многоатомного газа в общем случае м. б.
представлена суммой вкладов от отдельных видов движения-поступательного, вращательного, колебательного.
Поступательная теплоемкость рассчитывается так же, как для одноатомного газа. Вращательная и в особенности колебательная теплоемкость должны, как правило, вычисляться на основе квантовой статистики. Согласно классич.
статистике, вклады в молярную теплоемкость в расчете на одну степень свободы равны: для вращат. движения R/2, для колебат. движения R. Для большинства молекул при низких и средних т-рах колебат. степени свободы вырождены и не дают вклада в теплоемкость. Напр.
, теплоемкость двухатомного газа при обычных т-рах равна 5R/2. Лишь при достаточно высоких т-рах возбуждаются колебания определенной частоты.
Теплоемкость твердых тел. При низких т-рах теплоемкость одноатомных кристаллов пропорциональна кубу абс. т-ры (закон Дебая): СV ! Т3. При высоких т-рах СV стремится к предельному значению 3R, определяемому классич. теорией и не зависящему от природы атомов (правило Дюлонга и Пти).
Значение 3R может, однако, не достигаться, если ранее происходит плавление в-ва или его разложение. Методами квантовой статистики доказывается равенство нулю теплоемкости любого тела при абс. нуле т-ры (CV : 0 при Т : 0).
Если бы это было не так, энтропия системы, согласно (2), должна была бы обращаться в — , при T : 0, что противоречит третьему началу термодинамики (см. Тепловая теорема). Предельное значение СV = 3R достигается уже при обычных т-рах у металлов. Для нек-рых простых соед.
с числом атомов в молекуле n предельное значение CV = 3nR [NaCl, MnS (n = = 2), РbСl2(n = 3) и др.].
Для кристаллич. твердых тел существует характеристич. т-ра qD, названная т-рой Дебая, разделяющая «классич. область» т-р ТqD, в к-рой теплоемкость описывается законом Дюлонга и Пти, и «квантовую область» TqD. Т-ра Дебая связана с предельной частотой колебаний атомов в кристал-лич. решетке и зависит от упругих постоянных в-ва (см. табл.).
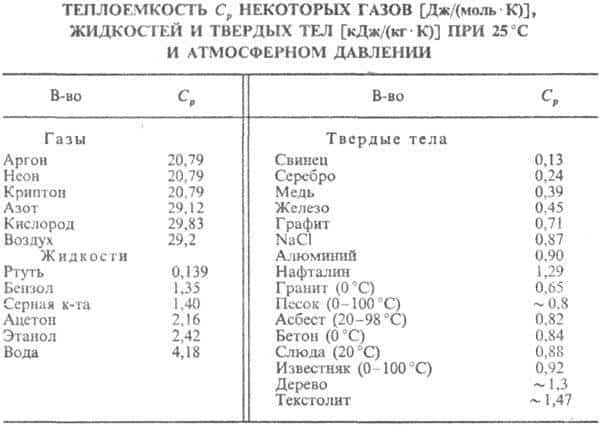
У металлов вклад в значение СV дают электроны проводимости (электронная теплоемкость). Эта часть теплоемкости может быть вычислена на основе квантовой статистики Ферми, к-рой подчиняются электроны.
Электронная теплоемкость пропорциональна т-ре в первой степени, однако ее вклад пренебрежимо мал при т-рах, когда велика «решеточная» теплоемкость (пропорциональная T3). Антиферромагнетики и ферримагнетики, обладающие упорядоченным расположением спиновых магн. моментов атомов, имеют дополнит. магн.
составляющую теплоемкости, к-рая испытывает резкий подъем при т-ре фазового перехода в-ва в парамагнитное состояние (см. Кюри точка).
Методы определения теплоемкости индивидуальных веществ. Осн. эксперим. методом является калориметрия. Теоретич. расчет теплоемкости в-в осуществляется методами статистической термодинамики, но он возможен только для сравнительно простых молекул в состоянии идеального газа и для кристаллов, причем в обоих случаях для расчета требуются эксперим. данные о строении в-ва.
Эмпирич. методы определения теплоемкости в-в в состоянии идеального газа основаны на представлении об аддитивности вкладов отдельных групп атомов или хим. связей. Опубликованы обширные таблицы групповых атомных вкладов в значение Ср.
Для жидкостей, помимо аддитивно-групповых, применяют методы, основанные на соответственных состояний законе, а также на использовании термодинамич.
циклов, позволяющих перейти к теплоемкости жидкости от теплоемкости идеального газа через температурную производную энтальпии испарения.
Для р-ра вычисление теплоемкости как аддитивной ф-ции теплоемкости компонентов в общем случае некорректно, т.к. избыточная теплоемкость р-ра, как правило, значительна.
Для ее оценки требуется привлечение молекулярно-статистич. теории р-ров (см. Растворы неэлектролитов).
Экспериментально избыточная теплоемкость может быть определена по температурной зависимости энтальпии смешения, после чего возможен расчет Ср р-ра.
Теплоемкость гетерог. систем представляет наиб. сложный случай для термодинамич. анализа. На диаграмме состояния перемещение вдоль кривой равновесия фаз сопровождается изменением и р, и Т. Если в процессе нагрева происходит смещение точки фазового равновесия, то это дает дополнит.
вклад в теплоемкость, поэтому теплоемкость гетерог. системы не равна сумме теплоемкостей составляющих ее фаз, но превосходит ее. На фазовой диаграмме при переходе от гомог. состояния к области существования гетерог. системы теплоемкость испытывает скачок (см. Фазовые переходы).
Практическое значение исследований теплоемкости важно для расчетов энергетич. балансов процессов в хим. реакторах и др. аппаратах хим. произ-ва, а также для выбора оптим. теплоносителей. Эксперим.
измерение теплоемкости для разных интервалов т-р-от предельно низких до высоких-является осн. методом определения термодинамич. св-в в-в.
Для расчета энтальпий и энтропии в-ва (в интервалах от 0 до Т) используют интегралы от теплоемкости.:
к к-рым добавляютсясоответствующие эффекты фазовых переходов. Знание теплоемкости реагентов в нек-ром интервале т-р позволяет осуществить расчет теплового эффекта р-ции (см. Кирхгофа уравнение), а знание теплоемкости р-ров-рассчитать их термодинамич. св-ва при любой т-ре в пределах исследованного интервала.
Особо следует подчеркнуть роль теплоемкости в структурных исследованиях индивидуальных в-в в конденсир. состоянии и р-ров. Величины, являющиеся второй производной потенциалов Гиббса или Гельмгольца по параметрам состояния (а теплоемкость относится к таковым), весьма чувствительны к структурным изменениям системы.
В твердых телах и сплавах при фазовых переходах 2-го рода типа порядок — беспорядок наблюдаются l-образные скачки теплоемкости. В жидкостях такие скачки имеют место вблизи критич. точек равновесия жидкость-газ и жидкость-жидкость (см. Критические явления). В жидкости, напр., при нагр.
часть энергии может идти не на возбуждение новых степеней свободы молекул, а на изменение потенц. энергии взаимодействующих молекул. Этот вклад наз. «конфигурационной» теплоемкостью; она связана с характером мол. упорядочения в жидкостях и р-рах. В биохимии политермич.
измерения теплоемкости дают информацию о структурных переходах в белках.
Лит.: Рид Р., Праусниц Дж., Шервуд Т., Свойства газов и жидкостей, пер. с англ., 3 изд., Л., 1982; Шульц М. М., Филиппов В. К., «Ж. Весе. хим. об-ва им. Д.И. Менделеева», 1982, т. 27, с. 485-94; Панов М.Ю., Белоусов В. П., в сб.
: Химия и термодинамика растворов, в. 5, Л., 1982, с. 56-87; Термодинамические свойства индивидуальных веществ, под ред. В. П. Глушко, 3 изд., т. 1-4, М., 1978-82; Experimental thermodynamics, ed. by J. P. McCullough, D. W. Scott, v. 1, N. Y. — L.
, 1968. M. Ю. Панов.
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
Теплоемкость
выберите первую букву в названии статьи: А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
Теплоемкость, количество теплоты, затрачиваемое для изменения температуры на 1°С. Согласно более строгому определению, теплоемкость — термодинамическая величина, определяемая выражением:
где ΔQ — количество теплоты, сообщенное системе и вызвавшее изменение ее температуры на Delta;T. Отношение конечных разностей ΔQ/ΔТ называется средней теплоемкостю, отношение бесконечно малых величин dQ/dT — истинной теплоемкостю.
Поскольку dQ не является полным дифференциалом функции состояния, то и теплоемкость зависит от пути перехода между двумя состояниями системы. Различают теплоемкость системы в целом (Дж/К), удельную теплоемкость [Дж/(г·К)], молярную теплоемкость [Дж/(моль·К)].
Во всех ниже приведенных формулах использованы молярные величины теплоемкости.
Из второго начала термодинамики следует, что теплоемкость пропорциональна производной от энтропии системы S по температуре Т при постоянстве внешней силы или термодинамической координаты (обозначается индексом z):
- Наиболее важными видами теплоемкости являются теплоемкость CV при постоянном объеме V и теплоемкость Ср при постоянном давлении р:
- СV=(∂U/∂T)V=T(∂S/∂T)V, Ср=(∂Н/∂Т)р=Т(∂S/∂Т)р,
- где U — внутренняя энергия, H — энтальпия системы. Значения Ср и СV связаны соотношением:
где a=V-1(∂V/∂Т)р — коэффициент термического расширения, x=—V-1(∂V/∂р)T — коэффициент изотермической сжимаемости. Поскольку по условиям устойчивости фаз Ср, CV>0 и (∂V/∂р)TCV. Это естественно, т.к.
при изобарическом нагревании часть тепла, помимо увеличения внутренней энергии системы, идет на работу расширения. Для идеальных газов (∂U/∂V)T=0 и учет уравнения состояния pV=RT приводит к соотношению: Сp-CV=R (R — газовая постоянная).
Для адиабатического процесса С =0.
Теплоемкость газов
Вычисление теплоемкости сводится к вычислению средней энергии теплового движения отдельных молекул, которое складывается из поступательных и вращательных движений молекулы как целого и из колебаний атомов внутри молекулы.
Молярная теплоемкость одноатомного газа равна 3R/2 (по R/2 на каждую степень поступательного движения молекулы).
Теплоемкость многоатомного газа в общем случае может быть представлена суммой вкладов от отдельных видов движения — поступательного, вращательного, колебательного.
Поступательная теплоемкость рассчитывается так же, как для одноатомного газа. Вращательная и в особенности колебательная теплоемкости должны, как правило, вычисляться на основе квантовой статистики.
Согласно классической статистике, вклады в молярную теплоемкость в расчете на одну степень свободы равны: для вращательного движения R/2, для колебательного движения R.
Для большинства молекул при низких и средних температурах колебательные степени свободы вырождены и не дают вклада в теплоемкость Например, теплоемкость двухатомного газа при обычных температурах равна 5R/2. Лишь при достаточно высоких температурах возбуждаются колебания определенной частоты.
Теплоемкость твердых тел
При низких температурах теплоемкость одноатомных кристаллов пропорциональна кубу абсолютной температуры (закон Дебая): СV ~ Т3. При высоких температурах СV стремится к предельному значению 3R, определяемому классической теорией и не зависящему от природы атомов (правило Дюлонга и Пти).
Значение 3R может, однако, не достигаться, если ранее происходит плавление вещества или его разложение. Методами квантовой статистики доказывается равенство нулю теплоемкости любого тела при абсолютном нуле температуры (CV: 0 при Т: 0).
Если бы это было не так, энтропия системы, согласно (2), должна была бы обращаться в — , при T: 0, что противоречит третьему началу термодинамики (см. Тепловая теорема). Предельное значение СV=3R достигается уже при обычных температурах у металлов.
Для некоторых простых соединений с числом атомов в молекуле n предельное значение CV=3nR [NaCl, MnS (n=2), РbСl2 (n=3) и др.].
Для кристаллических твердых тел существует характеристическая температура qD, названная температурой Дебая, разделяющая «классичесскую область» температур Т qD, в которой теплоемкость описывается законом Дюлонга и Пти, и «квантовую область» T qD. Температура Дебая связана с предельной частотой колебаний атомов в кристаллической решетке и зависит от упругих постоянных вещества (см. табл.).
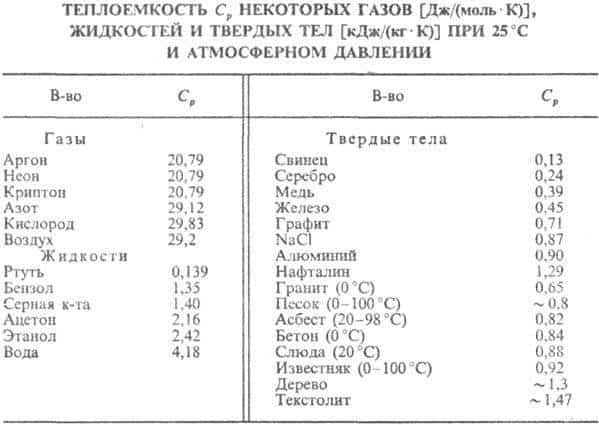
У металлов вклад в значение СV дают электроны проводимости (электронная теплоемкость). Эта часть теплоемкости может быть вычислена на основе квантовой статистики Ферми, которой подчиняются электроны.
Электронная теплоемкость пропорциональна температуре в первой степени, однако ее вклад пренебрежимо мал при температурах, когда велика «решеточная» теплоемкость (пропорциональная T3).
Антиферромагнетики и ферримагнетики, обладающие упорядоченным расположением спиновых магнитных моментов атомов, имеют дополнительную магнитную составляющую теплоемкости, которая испытывает резкий подъем при температуре фазового перехода вещества в парамагнитное состояние (см. Кюри точка).
Методы определения теплоемкость индивидуальных веществ
Основным экспериментальным методом является калориметрия. Теоретический расчет теплоемкости веществ осуществляется методами статистической термодинамики, но он возможен только для сравнительно простых молекул в состоянии идеального газа и для кристаллов, причем в обоих случаях для расчета требуются экспериментальные данные о строении вещества.
Эмпирические методы определения теплоемкости веществ в состоянии идеального газа основаны на представлении об аддитивности вкладов отдельных групп атомов или химических связей. Опубликованы обширные таблицы групповых атомных вкладов в значение Ср.
Для жидкостей, помимо аддитивно-групповых, применяют методы, основанные на соответственных состояний законе, а также на использовании термодинамических циклов, позволяющих перейти к теплоемкости жидкости от теплоемкости идеального газа через температурную производную энтальпии испарения.
Для раствора вычисление теплоемкости как аддитивной функции теплоемкостей компонентов в общем случае некорректно, т.к. избыточная теплоемкость раствора, как правило, значительна.
Для ее оценки требуется привлечение молекулярно-статистической теории растворов (см. Растворы неэлектролитов).
Экспериментально избыточная теплоемкость может быть определена по температурной зависимости энтальпии смешения, после чего возможен расчет Ср р-ра.
Теплоемкость гетерогенных систем представляет наиболее сложный случай для термодинамического анализа.
На диаграмме состояния перемещение вдоль кривой равновесия фаз сопровождается изменением и р, и T/ Если в процессе нагрева происходит смещение точки фазового равновесия, то это дает дополнительный вклад в теплоемкость, поэтому теплоемкость гетерогенной системы не равна сумме теплоемкостей составляющих ее фаз, но превосходит ее. На фазовой диаграмме при переходе от гомогенного состояния к области существования гетерогенной системы теплоемкость испытывает скачок (см. Фазовые переходы).
Практическое значение исследований теплоемкости важно для расчетов энергетических балансов процессов в химических реакторах и др. аппаратах химического производства, а также для выбора оптимальных теплоносителей.
Экспериментальное измерение теплоемкости для разных интервалов температур — от предельно низких до высоких — является основным методом определения термодинамических свойств веществ.
Для расчета энтальпий и энтропии вещества (в интервалах от 0 до Т) используют интегралы от теплоемкости:
к которым добавляются соответствующие эффекты фазовых переходов. Знание теплоемкости реагентов в некотором интервале температур позволяет осуществить расчет теплового эффекта реакции (см. Кирхгофа уравнение), а знание теплоемкостей растворов — рассчитать их термодинамические свойства при любой температуре в пределах исследованного интервала.
Особо следует подчеркнуть роль теплоемкости в структурных исследованиях индивидуальных веществ в конденсированном состоянии и растворов. Величины, являющиеся второй производной потенциалов Гиббса или Гельмгольца по параметрам состояния (а теплоемкость относится к таковым), весьма чувствительны к структурным изменениям системы.
В твердых телах и сплавах при фазовых переходах 2-го рода типа порядок — беспорядок наблюдаются l-образные скачки теплоемкости. В жидкостях такие скачки имеют место вблизи критических точек равновесия жидкость-газ и жидкость-жидкость (см. Критические явления).
В жидкости, например, при нагревании часть энергии может идти не на возбуждение новых степеней свободы молекул, а на изменение потенциальной энергии взаимодействующих молекул. Этот вклад называется «конфигурационной» теплоемкостью; она связана с характером молекулярного упорядочения в жидкостях и растворах.
В биохимии политермические измерения теплоемкости дают информацию о структурных переходах в белках.
Лит.: Рид Р., Праусниц Дж., Шервуд Т., Свойства газов и жидкостей, пер. с англ., 3 изд., Л., 1982; Шульц М.М., Филиппов В.К., «Ж. Всес. Хим. об-ва им. Д.И. Менделеева», 1982, т. 27, с. 485-94; Панов М.Ю., Белоусов В.П., в сб.
: Химия и термодинамика растворов, в. 5, Л., 1982, с. 56-87; Термодинамические свойства индивидуальных веществ, под ред. В.П.Глушко, 3 изд., т. 1-4, М., 1978-82; Experimental thermodynamics, ed. by J.P.McCullough, D.W.Scott, v. 1, N. Y. — L.
, 1968.
© M. Ю. Панов.
выберите первую букву в названии статьи: А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
Удельная и молярная теплоёмкости
Удельной теплоемкостью вещества называется физическая величина, численно равная количеству энергии в форме теплоты, которое надо сообщить единице массы этого вещества для увеличения его температуры на 1 Кельвин (т.е. это теплоёмкость, отнесённая к единице массы вещества):
В общем случае удельная теплоемкость зависит от рода вещества и от вида термодинамического процесса, в котором телу сообщается количество теплоты.
Удельные теплоёмкости многих веществ приведены в справочниках (обычно для процесса при постоянном давлении). К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда – 2100 Дж/(кг·К).
Количество теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их температуры), но и от способа, которым был осуществлен процесс перехода между ними.
Поэтому для газов различают два вида теплоемкостей: если газ нагревают, сохраняя его объем постоянным (изохорно), говорят об удельной теплоемкости газа при постоянном объеме cV; если же газ нагревают, сохраняя постоянным его давление (изобарно), то говорят об удельной теплоемкости газа при постоянном давлении сР. У жидкостей и твёрдых тел разница между Ср и Cv сравнительно мала.
Часто пользуются молярной теплоемкостью Сμ, которая, в отличие от удельной теплоемкости, отнесена не к единице массы (1 килограмму), а к массе одного моля вещества. Очевидно, что
Cμ = mc, Дж/(моль×К)
Для газов молярную теплоемкость, рассчитанную при постоянном давлении, обозначают СР, а рассчитанную при постоянном объеме – СV. Следовательно, СР = m×cP, CV = m×cV.
Когда нагревание газа происходит при постоянном объеме, газ не совершает механической работы и все сообщаемое газу тепло идет только на увеличение его внутренней энергии DU, т.е.:
DQ = m×cV×DT = DU.
Если же нагревание газа происходит при постоянном давлении и, следовательно, объем газа увеличивается, то сообщаемое газу тепло DQ идет как на увеличение его внутренней энергии DU, так и на совершение газом работы DA над внешними телами, т.е. DQ = m×cP×DT = DU + DA.
Из сопоставления формул следует, что cP > cV, т.е. удельная теплоемкость газа при постоянном давлении больше удельной теплоемкости того же газа при постоянном объеме. При этом, согласно уравнению Майера:
CP = CV + R.
В данной работе требуется определить не абсолютные значения теплоемкостей газа, а их отношение, называемое коэффициентом Пуассона:
Теоретическое вычисление теплоемкости, в частности её зависимости от температуры тела, не может быть осуществлено с помощью чисто термодинамических методов и требует применения методов статистической физики.
Молярная теплоёмкость | это… Что такое Молярная теплоёмкость?
- Теплоёмкость — {{{Название}}} Размерность L2MT −2Θ−1 Единицы измерения … Википедия
- Изобарная теплоёмкость — Теплоёмкость тела (обозначается C) физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: Единица измерения теплоёмкости в системе СИ Дж/К.… … Википедия
- ТЕПЛОЁМКОСТЬ — физ. величина, характеризующая тепловые свойства тела и равная отношению количества теплоты, полученного телом при бесконечно малом изменении его состояния в каком либо процессе, к вызванному им изменению температуры, т. е. теплоёмкость С = d Q/d … Большая политехническая энциклопедия
- Теплоёмкость идеального газа — Теплоемкость идеального газа это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло. Содержание 1 Молярная теплоемкость … Википедия
- ТЕПЛОЁМКОСТЬ — величина, равная отношению количества теплоты dQ, сообщаемому телу, к соответствующему изменению температуры Т этого тела: C=dQ/dT. Отношение теплоёмкости к массе m тела называют удельной теплоёмкостью: с=С/m; отношение теплоёмкости к количеству… … Металлургический словарь
- ТЕПЛОЁМКОСТЬ — величина, равная отношению кол ва теплоты бQ, сообщаемого телу (системе) при бесконечно малом изменении его состояния в к. л. процессе, к соответствующему изменению темп ры Т этого тела: С = бQ/dT. Отношение Т. к массе тела т наз. удельной Т.: с … Большой энциклопедический политехнический словарь
- Объёмная теплоёмкость — характеризует способность данного объёма вещества увеличивать свою внутреннюю энергию при изменении температуры вещества без осуществления фазового перехода. Объёмная теплоёмкость отличается от удельной теплоёмкости, которая характеризует… … Википедия
- Изобарная теплоемкость — Теплоёмкость тела (обозначается C) физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: Единица измерения теплоёмкости в системе СИ Дж/К.… … Википедия
- Теорема о равнораспределении — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
- Закон равнораспределения — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия
Теплоёмкость
Ещё одним параметром, характеризующим тепловую систему, является параметр теплоёмкости. Теплоёмкостью называется отношение тепла, полученного/отданного системой (телом), к изменению температуры системы (тела) в этом процессе:
- где
- — теплоёмкость системы,
- — теплота, принятая/отданная системой,
- — изменение температуры в этом процессе.
Теплоёмкость (1) характеризует конкретную систему, однако для чистых газов, жидкостей и твёрдых тел можно унифицировать данный параметр и сделать его табличным. С этой целью вводятся:
- где
- — удельная теплоёмкость вещества,
- — теплота, принятая/отданная системой,
- — масса вещества,
- — изменение температуры в этом процессе.
Удельной теплоёмкостью, в таком случае, называется теплоёмкость единицы массы вещества ( т.е. теплоёмкость одного килограмма вещества). Размерность — [Дж/(кг*К)] (Джоуль на килограмм на Кельвин).
(3)
- где
- — молярная теплоёмкость вещества,
- — теплота, принятая/отданная системой,
- — химическое количество вещества,
- — изменение температуры в этом процессе.
Молярной теплоёмкостью, в таком случае, называется теплоёмкость единицы моля вещества (т.е. теплоёмкость одного моля вещества). Размерность — [Дж/(моль*К)] (Джоуль на моль на Кельвин).
Используем первое начало термодинамики в развёрнутом виде:
(4)
- где
- — теплота полученная/отданная газом,
- — давление газа,
- — изменение объёма газа,
- — химическое количество газа,
- м*кг*с*К*Моль — газовая постоянная,
- — изменение температуры газа.
- Подставим (4) в (3):
- = (5)
- Соотношение (5), в некотором смысле, упрощает решение ряда задач.
- Вывод: большинство задач на теплоёмкость связаны с поиском теплоты, связанной с системой и конкретными процессами (5).






