Дислокация металла что это

Что такое дислокация? Виды дислокаций и их влияние на механические свойства металла. В любом реальном кристалле всегда имеются дефекты строения.

Ли­нейные несовершенства имеют малые размеры в двух измерениях и большую протяженность в третьем. Эти несовершенства называются дислокациями.

Краевая дислокация представляет собой линию, вдоль которой обры­вается внутри кристалла край “лишней“ полуплоскости (рисунок 1)

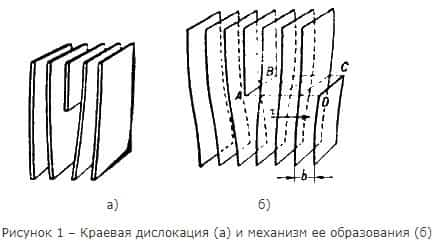Неполная плоскость называется экстраплоскостью. Большинство дислокаций образуются путем сдвигового механизма. Ее образование можно описать при помощи следующей операции. Надрезать кристалл по плоскости АВСD, сдвинуть нижнюю часть относительно верх­ней на один период решетки в направлении, перпендикулярном АВ, а затем вновь сблизить атомы на краях разреза внизу. Наибольшие искажения в расположении атомов в кристалле имеют ме­сто вблизи нижнего края экстраплоскости. Вправо и влево от края экстра­плоскости эти искажения малы (несколько периодов решетки), а вдоль края экстраплоскости искажения простираются через весь кристалл и могут быть очень велики (тысячи периодов решетки) (рисунок 2). Если экстраплоскость находится в верхней части кристалла, то краевая дислокация – положительная (┴), если в нижней, то – отрицательная (┬). Дислокации одного знака отталкиваются, а противоположные притягива­ются. 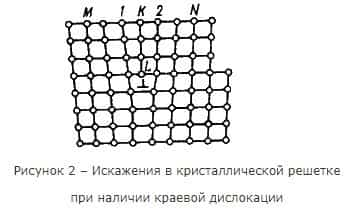Другой тип дислокаций был описан Бюргерсом, и получил название винтовая дислокация Винтовая дислокация получена при помощи частичного сдвига по плоскости Q вокруг линии EF (рисунок 3) На поверхности кристалла образу­ется ступенька, проходящая от точки Е до края кристалла. Такой частичный сдвиг нарушает параллельность атомных слоев, кристалл превращается в одну атомную плоскость, закрученную по винту в виде полого геликоида во­круг линии EF, которая представляет границу, отделяющую часть плоскости скольжения, где сдвиг уже произошел, от части, где сдвиг не начинался. Вдоль линии EF наблюдается макроскопический характер области несовер­шенства, в других направлениях ее размеры составляют несколько периодов. Если переход от верхних горизонтов к нижним осуществляется поворо­том по часовой стрелке, то дислокация правая, а если поворотом против ча­совой стрелки – левая. 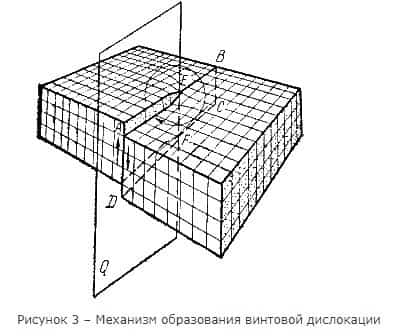Винтовая дислокация не связана с какой-либо плоскостью скольжения, она может перемещаться по любой плоскости, проходящей через линию дис­локации. Вакансии и дислоцированные атомы к винтовой дислокации не сте­кают. В процессе кристаллизации атомы вещества, выпадающие из пара или раствора, легко присоединяются к ступеньке, что приводит к спиральному механизму роста кристалла. Линии дислокаций не могут обрываться внутри кристалла, они должны либо быть замкнутыми, образуя петлю, либо разветвляться на несколько дис­локаций, либо выходить на поверхность кристалла. Дислокационная структура материала характеризуется плотностью дислокаций. Плотность дислокаций в кристалле определяется как среднее число линий дислокаций, пересекающих внутри тела площадку площадью 1 м2, или как суммарная длина линий дислокаций в объеме 1 м3: 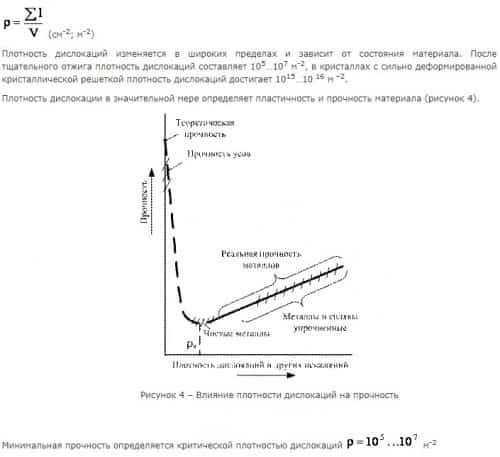Если плотность меньше значения а, то сопротивление деформирова­нию резко возрастает, а прочность приближается к теоретической. Повыше­ние прочности достигается созданием металла с бездефектной структурой, а также повышением плотности дислокаций, затрудняющим их движение. В настоящее время созданы кристаллы без дефектов – нитевидные кристаллы длиной до 2 мм, толщиной 0,5…20 мкм – «усы» с прочностью, близкой к теоретической: для железа σВ = 13000 МПа, для меди σВ =30000 МПа. При упрочнении металлов увеличением плотности дислокаций, она не должна превышать значений 1015…1016м–2. В противном случае образуются тре­щины. Дислокации влияют не только на прочность и пластичность, но и на другие свойства кристаллов. С увеличением плотности дислокаций возрас­тает внутреннее, изменяются оптические свойства, повышается электросо­противление металла. Дислокации увеличивают среднюю скорость диффузии в кристалле, ускоряют старение и другие процессы, уменьшают химическую стойкость, поэтому в результате обработки поверхности кристалла специаль­ными веществами в местах выхода дислокаций образуются ямки. Дислокации образуются при образовании кристаллов из расплава или газообразной фазы, при срастании блоков с малыми углами разориентировки. При перемещении вакансий внутри кристалла, они концентрируются, обра­зуя полости в виде дисков. Если такие диски велики, то энергетически вы­годно «захлопывание» их с образованием по краю диска краевой дислокации. Образуются дислокации при деформации, в процессе кристаллизации, при термической обработке.

Полосы свинца были прокатаны при комнатной температуре с различной степенью обжатия: 10, 20, 40, 60%. После прокатки твердость всех листов оказалась практически неизменной. Объясните, почему не наблюдается упрочнение свинца при деформации в этих условиях. Какими процессами сопровождается деформирование свинца при комнатной температуре?

По правилу А.А. Бочвара можно оценить в первом приближении температурный порог рекристаллизации по известной температуре плавления металла: Тп.р.=0,4 Тпл. Температура начала рекристаллизации свинца: Тп.р.=(327+273)0,4-273=-33°С. Таким образом, комнатная температура превышает температуру начала рекристаллизации. Лист свинца подвергся горячей пластической деформации. Деформация называется горячей, если ее проводят при температуре выше температуры рекристаллизации для получения полностью рекристаллизованной структуры. При этих температурах деформация вызывает упрочнение («горячий наклеп»), которое снимается рекристаллизацией, протекающей при температурах обработки и при последующем охлаждении. Поэтому свойства листа свинца в результате не изменились.

Вычертите диаграмму состояния железо – карбид железа, укажите структурные составляющие во всех областях диаграммы, опишите превращения и постройте кривую охлаждения (с применением правила фаз) для сплава, содержащего 0,01% С. Какова структура этого сплава при комнатной температуре и как такой сплав называется?

Первичная кристаллизация сплавов системы железо-углерод начинается по достижении температур, соответствующих линии ABCD (линии ликвидус), и заканчивается при температурах, образующих линию AHJECF (линию солидус). При кристаллизации сплавов по линии АВ из жидко­го раствора выделяются кристаллы твердого раствора углерода в α-железе (δ-раствор). Процесс кристаллиза­ции сплавов с содержанием углерода до 0,1 % заканчи­вается по линии АН с образованием α (δ)-твердого раст­вора. На линии HJB протекает перитектическое превращение, в результате которого образуется твердый раствор углерода в γ-железе, т. е. аустенит. Процесс первичной кристаллизации сталей заканчивается по линии AHJE. При температурах, соответствующих линии ВС, из жидкого раствора кристаллизуется аустенит. В сплавах, содержащих от 4,3 % до 6,67 % углерода, при темпера­турах, соответствующих линии CD, начинают выделяться кристаллы цементита первичного. Цементит, кристал­лизующийся из жидкой фазы, называется первичным. B точке С при температуре 1147°С и концентрации углерода в жидком растворе 4,3 % образуется эвтектика, которая называется ледебуритом. Эвтектическое превращение с образованием ледебурита можно записать формулой ЖР4,3Л[А2,14+Ц6,67]. Процесс первичной кристаллизации чугунов заканчивается по линии ECF образованием ледебурита. Таким образом, структура чугунов ниже 1147°С будет: доэвтектических – аустенит+ледебурит, эвтектических – ледебурит и заэвтектических – цементит (первичный)+ледебурит. Превращения, происходящие в твердом состоянии, называются вторичной кристаллизацией. Они связаны с переходом при охлаждении γ-железа в α-железо и распадом аустенита. Линия GS соответствует температурам начала превращения аустенита в феррит. Ниже линии GS сплавы состоят из феррита и аустенита. Линия ЕS показывает температуры начала выделения цементита из аустенита вследствие уменьшения растворимости углерода в аустените с понижением температуры. Цементит, выделяющийся из аустенита, называется вторичным цементитом. В точке S при температуре 727°С и концентрации углерода в аустените 0,8 % образуется эвтектоидная смесь состоящая из феррита и цементита, которая называется перлитом. Перлит получается в результате одновременного выпадения из аустенита частиц феррита и цементита. Процесс превращения аустенита в перлит можно записать формулой А0,8П[Ф0,03+Ц6,67]. Линия PQ показывает на уменьшение растворимости углерода в феррите при охлаждении и выделении цементита, который называется третичным цементитом. Следовательно, сплавы, содержащие менее 0,008% углерода (точкаQ), являются однофазными и имеют структуру чистого феррита, а сплавы, содержащие углерод от 0,008 до 0,03% – структуру феррит+цементит третичный и называются техническим железом. Доэвтектоидные стали при температуре ниже 727ºС имеют структуру феррит + перлит и заэвтектоидные – перлит + цементит вторичный в виде сетки по границам зерен. В доэвтектических чугунах в интервале температур 1147–727ºС при охлаждении из аустенита выделяется цементит вторичный, вследствие уменьшения растворимости углерода(линия ES). По достижении температуры 727ºС (линия PSK) аустенит, обедненный углеродом до 0,8% (точка S), превращаясь в перлит. Таким образом, после окончательного охлаждения структура доэвтектических чугунов состоит из перлита, цементита вторичного и ледебурита превращенного (перлит+цементит). Структура эвтектических чугунов при температурах ниже 727ºС состоит из ледебурита превращенного. Заэвтектический чугун при температурах ниже 727ºС состоит из ледебурита превращенного и цементита первичного. Правило фаз устанавливает зависимость между числом степеней свободы, числом компонентов и числом фаз и выражается уравнением: C = K + 1 – Ф, где С – число степеней свободы системы; К – число компонентов, образующих систему; 1 – число внешних факторов (внешним фактором считаем только температуру, так как давление за исключением очень высокого мало влияет на фазовое равновесие сплавов в твердом и жидком состояниях); Ф – число фаз, находящихся в равновесии. Сплав железа с углеродом, содержащий 0,01%С, называется доэвтектоидной сталью. Его структура при комнатной температуре – Феррит + Цементит (первичный).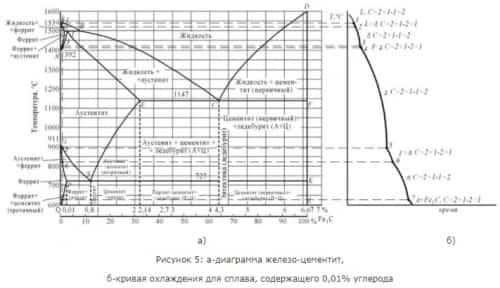

Вычертите диаграмму изотермического превращения аустенита для стали У8. Нанесите на нее кривую режима термической обработки, обеспечивающей твердость 350 НВ. Опишите сущность превращений и какая структура получается при этой обработке.

Термической обработкой, необходимой для получения твердости 350 НВ, является изотермическая закалка на троостит. В качестве охлаждающей среды при изотермической закалке чаще всего применяют расплавленные соли, интервал температур которых определяется экспериментально. При нагреве стали У8 выше А1 перлит переходит в аустенит. В результате охлаждения в расплавах солей из аустенита образуется ферритно-цементитная структура – троостит.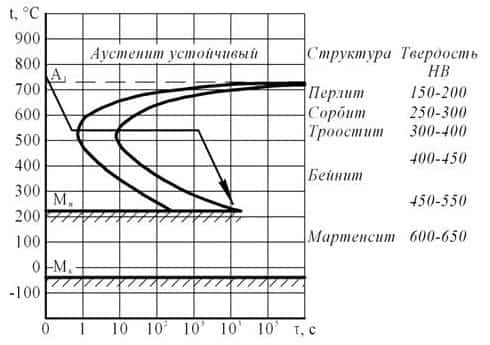 Рисунок 6 – Диаграмма изотермического превращения аустенита стали У8 В результате термической обработки получается твердость стали 350 НВ, структура – троостит.

Как изменяются структура и свойства стали 30 и У11 в результате закалки от температуры 750 и 850°С. Объясните с применением диаграммы состояния железо-цементит. Выберите оптимальный режим закалки каждой стали.

Исходная структура высокоуглеродистой инструментальной стали У11 до нагрева под закалку – перлит + карбиды. Критические точки для стали У11: Аc1=730ºС, Аcm=810ºС. Оптимальный режим нагрева под закалку для заэвтектоидных сталей (%С>0,8%) составляет АС1+(30÷50º), т.е. для У11 – 760–780ºС. При этом после закалки имеем мелкое зерно, обеспечивающее наилучшие механические свойства стали У11. Нагрев и выдержка стали У11 при температуре 850ºС перед закалкой приводит к росту зерна и ухудшению механических свойств стали после термической обработки. Крупнозернистая структура вызывает повышенную хрупкость стали, иногда приводит к трещинам. Закалка доэвтектоидной стали заключается в нагреве стали до температуры выше критической (Ас3), в выдержке и последующем охлаждении со скоростью, превышающей критическую. Температура точки Ас3 для стали 30 составляет 820°С. Если доэвтектоидную сталь нагреть выше Ас1, но ниже Ас3, то в ее структуре после закалки наряду с мартенситом будут участки феррита. Присутствие феррита как мягкой составляющей снижает твердость стали после закалки. При нагреве до температуры 750°С (ниже точки Ас3) структура стали 30 – аустенит + феррит, после охлаждения со скоростью выше критической структура стали – мартенсит + феррит.

Доэвтектоидные стали для закалки следует нагревать до температуры на 30-50°С выше Ас3. Температура нагрева стали под закалку, таким образом, составляет 850-870°С. Структура стали 30 при температуре нагрева под закалку – аустенит, после охлаждения со скоростью выше критической – мартенсит.

Лекция 5. Основные типы дислокаций: краевые, винтовые и смешанные дислокации

Основные типы дислокаций: краевые, винтовые и смешанные дислокации. Вектор Бюргерса. Перемещение дислокаций скольжением и переползанием.

Дислокации принадлежат к линейным несовершенствам кристалла. Первоначально представления о дислокации были введены в физику твёрдого тела в 1934 году для того, чтобы объяснить несоответствие между наблюдаемой и теоретической прочностью и описать атомный механизм скольжения при пластической деформации кристаллов.

Численные теоретические значения скалывающих напряжений, необходимых для деформации оказываются больше экспериментальных в 10- 10раз. Такая разница между расчётной и экспериментальной величинами свидетельствует о том, что механизм процесса сдвига при деформации, основанный на предположении, что части кристалла при этом смещаются относительно друг друга вдоль плоскости скольжения как жесткие системы, не соответствует реальности. Это объясняется тем, что в кристалле, находящемся под внешним напряжением, взаимодействуют уже существующие в нём и возникающие под воздействием внешнего напряжения особого рода дефекты кристаллической решётки. Впоследствии теория дислокаций получила широкое развитие и стала применяться для анализа самых разнообразных явлений в металлах и сплавах. При этом, если на первых этапах развития этой теории представления о дислокациях были чисто гипотетическими, то затем были получены прямые доказательства их существования, а в настоящее время используются разнообразные экспериментальные методы изучения дислокаций в металлах и сплавах.

Схема краевой дислокации показана на рис.20. Если в кристалле сделать надрез по плоскости АВСД и сдвинуть части кристалла вдоль плоскости надреза, перпендикулярно к краю надреза, что полученная граница АВ между участком, где скольжение уже произошло, и ненарушенным участком будет краевой дислокацией (рис.20.а).

Представим себе, что в части кристалла по каким либо причинам появилась лишняя полуплоскость атомов, так называемая экстраплоскость. Вблизи края экстраплоскости решётка сильно искажена. В этом участке кристаллов против n атомов одного ряда располагается n+1 или n-1 атомов другого ряда.

Выше края экстраплоскости (линия АВ) межатомные расстояния меньше параметра решётки, а ниже края – больше. Атом на самой кромке экстраплоскости имеет меньше соседей, чем внутри совершенной решётки.

Таким образом, вдоль края экстраплоскости находится область с несовершенной решёткой, которая называется краевой дислокацией.

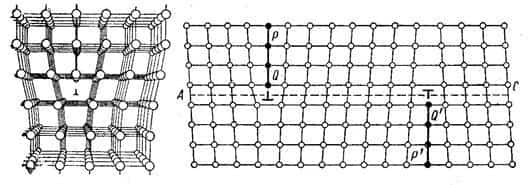
• Рисунок 20 – Краевая дислокация
• а – пространственная схема,
• б – схема расположения атомов в области дислокации

Ядром или центром дислокации называют осевую зону дефектного участка кристалла, где очень сильны искажения решётки.

Положение ядра дислокации в кристаллографической плоскости, являющейся плоскостью чертежа, обозначается знаком. Совокупность таких центров в параллельных атомных плоскостях образует линию дислокации.

Еслиэкстраплоскость находится в верхней части кристалла, то дислокацию называют положительной, в нижней – отрицательной. Положение центра ядра отрицательной краевой дислокации обозначается знаком . Дислокация перемещается в плоскости АВ, называемой плоскостью скольжения.

Большое значение в теории прочности и пластичности металлов имеет характер искажений кристаллической решётки вокруг краевой дислокации. У положительной краевой дислокации наблюдается растяжение кристаллической решётки под плоскостью скольжения, выше плоскости – сжатие решётки. У отрицательной дислокации наоборот.

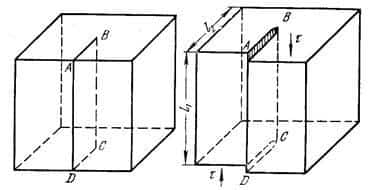Винтовая дислокация показана на рис.21. Если надрезать кристалл по плоскости АВСД и сдвинуть по этой плоскости одну часть кристалла относительно другой параллельно краю надреза, то границей сдвига окажется винтовая дислокация АВ (рис.21.а). Дефект решётки заключается в том, что одна её часть ( атомы изображены чёрными кружками) на некотором протяжении оказались сдвинутыми на один параметр решётки вниз по отношению к другой (белые кружки). Благодаря такому сдвигу части кристаллической решётки образовалась спиральная или винтовая поверхность. В отличие от линейной дислокации, лишней атомной плоскости у винтовой дислокации нет. Искажение кристаллической решётки заключается в том, что вблизи дислокации атомы меняют своих ближайших соседей, в результате чего плоскости решётки изгибаются. Характер искажений зависит от знака винтовой дислокации. Если искажения решётки направлены по часовой стрелке винтовая дислокация называется правой, если против часовой стрелке – левой.

Рисунок 21 – Сдвиг, создавший винтовую дислокацию.

а – кристалл до сдвига надрезан по АВСD, б – кристалл после сдвига, АВСD – зона сдвига.

Дислокации смешанной ориентации наиболее распространены в металлах и сплавах. Зона сдвига АВС на рис.22 ограничена линией дислокации АС. Плоскость чертежа является плоскостью скольжения, чёрные кружки обозначают атомы, расположенные под плоскостью скольжения, белые – над ней. Вблизи точки А дислокация имеет винтовую ориентацию, около точки В – краевую.

Линия смешанной дислокации может оканчиваться на гранях кристалла, как это показано на рис.22, кроме того, возможно существование замкнутой петли внутри кристалла. Отдельные участки имеют чисто винтовую или краевую ориентацию, но, в основном, ориентация дислокаций смешанная.

Петля определяет границу зоны сдвига части кристалла (внутри петли) относительно области вне петли, не претерпевшей сдвиг.

1. Рисунок 22 – дислокация смешанной
2. ориентации.
3. Дислокации, находящиеся в кристаллической решётке зёрен и кристаллов, называют дислокациями решётки, или внутризеренными.

Геометрически дислокации характеризуются двумя параметрами: направлением линии дислокации и вектором Бюргерса (рис.23).

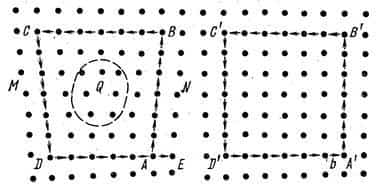
• Рисунок 23 – схема определения вектора Бюргерса
• а – схема плоскости реального кристалла,
• б – решётка совершенного кристалла.

Вектор Бюргерса является мерой искаженности кристаллической решётки, обусловленной присутствием в ней дислокации. Он определяет энергию дислокации, действующие на дислокации силы, величину, связанного с дислокацией сдвига, влияет на подвижность дислокации. Следовательно вектор Бюргерса главная количественная характеристика дислокации.

Если дислокация вводится в кристалл чистым сдвигом – так как это было показано ранее на примере краевой, винтовой дислокации, то вектор сдвига и является вектором Бюргерса. Вектор сдвига определяет величину и направление смещения атомов в той области, где сдвиг уже произошел, т.е.

определяет степень искаженности решётки, связанную с присутствием дислокации, введенной в кристалл путём сдвига. Однако дислокация не всегда называется сдвигом. Кроме того, не все типы дислокаций можно определять через вектор сдвига.

Поэтому более общим является определение вектора Бюргерса не как сдвига, а как меры искаженности кристаллической решётки.

Чтобы оценить степень искаженности кристаллической решётки, вызванной дислокацией, следует сравнить несовершенный кристалл, содержащий дислокацию, с совершенным кристаллом.

Для этого строят так называемый контур Бюргерса.

Контуром Бюргерса называется замкнутый контур произвольной формы, построенный в реальном кристалле путём последовательного обхода дефекта от атома к атому в совершенной области кристалла.

При одинаковом количестве шагов в горизонтальном и вертикальном направлении в конце концов приходим к первоначальному атому, т.е. в идеальном кристалле контур Бюргерса замкнут. В кристалле, содержащем краевую положительную дислокацию, контур Бюргерса окажется незамкнутым. Остаётся ещё отрезок, длина и направление которого определяют вектор Бюргерса.

На рис.24 показано построение контура и вектора Бюргерса для винтовой дислокации. Контур Бюргерса можно, например, построить от исходной точки А (рис.24.а).

Пройдём от неё влево девять межатомных расстояний до точки В, шесть до точки С и вправо девять до точки Д.

Чтобы попасть на уровень исходной точки А, опустимся от точки Д по вертикали вниз до точки Е на одно межатомное расстояние и пройдём шесть межатомных расстояний от Е доА.

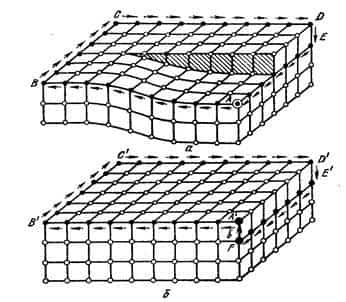
Рисунок 24 – Контур Бюргерса вокруг винтовой дислокации (а) и эквивалентный контур в совершенном кристалле (б)

Для проведения соответствующего контура к совершенном кристалле (рис 24.б) сделаем девять шагов от исходной точки Адо В, затем шесть до С, девять до Д, один шаг вниз по вертикали от Ддо Еи шесть шагов на горизонтальном уровне в сторону исходной точки. При этом мы попадём не в исходную точку А, а в точку F. Невязку контура ликвидируем, замыкая его вектором Бюргерса b (соединяя точки F и А). Этот вектор характеризует степень искаженности решётки, вызванной дислокацией в кристалле на рис.24а. Весьма удобно, что искаженность решётки несовершенного кристалла выражается через период решётки идеального кристалла, т.е. через константу.

Дислокации, у которых вектор Бюргерса соответствует тождественной трансляции атома, называются полными или единичными. Векторы единичных дислокаций имеют в решётке различные направления.

Энергия дислокаций будет минимальной в том случае, когда их векторы Бюргерса параллельны направлению плотнейшей упаковки атомов в кристаллической решётке.

Частичными являются такие дислокации, вектор Бюргерса не соответствует тождественной трансляции атома. Векторы Бюргерса частичных дислокаций меньше, чем полных.

Вектор Бюргерса характеризуется рядом особенностей:

1. Нормален к лини краевой дислокации и параллелен к линии винтовой дислокации. Вдоль линии смешанной дислокации угол между ней и вектором Бюргерса в разных точках имеет разную величину и располагается под углом к линии дислокации АС.

2. У дефектов недислокационного типа равен нулю. Если построить контур Бюргерса вокруг любого точечного или линейного дефекта недислокационного типа (вокруг цепочки атомов или вакансий), то соответствующий контур в идеальном кристалле окажется замкнутым.

3. Одинаков вдоль всей линии дислокации, т.е. является инвариантом дислокации.

Это следует, например, из того, что при смещении контура Бюргерса вдоль линии дислокации он всё равно будет оставаться эквивалентным исходному контуру (при условии, что он всеми своими точками не выходит из совершенной области решётки, т.е.

не пересекает другие несовершенства). Кроме того, вектор сдвига, создающего, например, криволинейную смешанную дислокацию, имеет одну величину и одно направление для всего кристалла.

Из инвариантности вектора Бюргерса вытекает важное следствие: дислокация не может обрываться внутри кристалла. Внутри кристалла дислокации могут образовывать замкнутые петли с одинаковыми векторами Бюргерса вдоль всей петли или встречаться с другими дислокациями, образовывая узлы (точки встречи).

Выход дислокаций на поверхность шлифа металла проявляется в виде точки – углубления. Дислокации являются местами развития растущего кристалла. Эти же места активны при обратном процессе – растворении.

К параметрам, характеризующим свойства дислокации относятся её длина и ширина. Длина дислокации – это протяженность зоны искажения кристаллической решётки. В чистых ГЦК металлах устойчивая дислокация при напряжениях, сравнимых с пределом текучести, может иметь длину 10-3 – 10-4 см.

Под шириной краевой дислокации следует понимать ширину области на плоскости скольжения, где величина межатомных смещений составляет не менее 1/8 максимального значения атомного смещения в центре дислокации, равного примерно 1/4а.

Ширина дислокации определяет её энергию, подвижность, уровень напряжений, при которых дислокация может двигаться вдоль плоскости скольжения.

Дислокации и их влияние на структуру материала

Дислокациями называют линейные дефекты кристаллов, возникающие в процессе роста или пластической деформации. Различают краевые и винтовые дислокации, нарушающие правильное чередование атомных плоскостей.

Причиной краевой дислокации является отрыв одной из плоскостей внутри кристалла. Образование винтовой дислокации связано, в основном, с условиями роста кристалла, состоящего из одной атомной плоскости, изгибающейся по винтовой поверхности.

Дислокации в кристалле могут возникать при его росте и в том случае, когда растущие навстречу друг другу блоки или зерна повернуты один относительно другого. При срастании таких блоков образуются избыточные атомные плоскости, которые определяют текстуру реальных кристаллов.

Причиной образования дислокаций в кристалле могут быть также скопления точечных дефектов, в частности, вакансий.

В процессе пластической деформации происходит не одновременный сдвиг всех атомов данной плоскости, а последовательное перемещение связей между атомами, лежащими по обе стороны плоскости скольжения. Такое перераспределение связей предопределяет движение дислокаций от одной группы атомов к другой.

Количество дислокаций в кристаллических структурах очень велико. Число дислокационных линий, пересекающих 1 см2 внутри отожженных монокристаллов может достигать 104¸106 и более.

Схемы образования дислокаций представлены на рис. 3.4 и рис. 3.5.

а б

Рис. 3.4.Образование дислокаций на границах блоков:

а – два блока, растущих навстречу друг другу; б— дислокации, возникающие при срастании блоков

а б

Рис. 3.5. Образование дислокаций из скопления вакансий:

а — скопление вакансий в кристалле; б – положительная и отрицательная дислокации

Наличие дислокаций значительно снижает прочность реальных кристаллов, которые разрушаются при напряжениях, на несколько порядков меньших, чем идеальные.

Дислокации влияют на электрические, оптические, магнитные и другие свойства. Так, они повышают электросопротивление, снижают плотность, упругость, а также предельное напряжение сдвига материала. Последнее объясняется тем, что при сдвиге, т.е. при пластической деформации к имеющимся дислокациям присоединяются и вновь образованные.

Однако пластическая деформация и рост дефектов могут привести к упрочнению структуры.

Это происходит в результате накопления дислокаций и взаимодействия их как между собой, так и с другими дефектами кристаллической решетки, что вызывает ее искажение и затрудняет перемещение дислокаций.

Кроме того, атомы примесей, границы блоков, обособленные включения в решетки также затрудняют перемещение дислокаций, увеличивая сопротивление сдвигу.

Напрашивается вывод о положительной роли дислокаций, тем более, что в металловедении известны многие практические приемы упрочнения структуры металлов, такие как холодное деформирование (наклеп), введение примесей (легирование), создание обособленных включений (закалка) и др.

Следовательно, для упрочнения кристаллической структуры необходимо стремиться либо к большему развитию дефектов, либо к полному их устранению. На рис. 3.6 представлен график влияния роста дефектов на изменение прочности кристаллической структуры, который показывает, что максимальная прочность реальных кристаллов далека от теоретической.

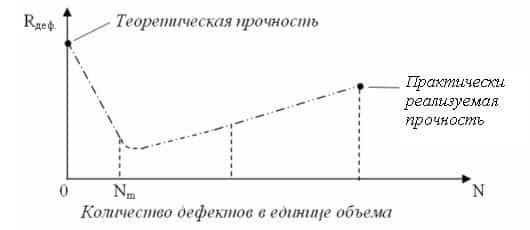
Рис. 3.6. Зависимость сопротивления деформации от количества дефектов в кристалле

В продолжение освещения роли линейных дефектов, образующихся в процессе пластических деформаций в кристаллической структуре, необходимо заметить о возможности локального скопления дислокаций, которые могут вызвать местные концентрации напряжений. Последние, в сочетании с такими же локальными скоплениями дефектов, способны образовывать зародыши микротрещин, которые, как известно, являются основной причиной разрушения структуры.

Роль поверхностных и объемных дефектов в структурообразовании рассмотрим при изучении макроструктуры материалов.

ДИСЛОКА́ЦИИ

Авторы: В. И. Альшиц, Б. В. Петухов

ДИСЛОКА́ЦИИ в кри­стал­лах (от ср.-век. лат. dis­lo­ca­tio – сме­ще­ние, пе­ре­ме­ще­ние), де­фек­ты кри­стал­ла, пред­став­ляю­щие со­бой на­ру­ше­ния в пра­виль­ном рас­по­ло­же­нии ато­мов, про­ис­хо­дя­щие в ок­рест­но­сти не­ко­то­рой ли­нии, про­ни­зы­ваю­щей кри­сталл. Впер­вые по­ня­тие Д. как то­по­ло­гич. ли­ней­но­го ис­точ­ни­ка внутр.

на­пря­же­ний в твёр­дом те­ле, рас­смат­ри­вае­мом как сплош­ная сре­да, бы­ло вве­де­но В. Воль­тер­рой в 1905. Од­на­ко нау­ка о Д. на­ча­ла раз­ви­вать­ся толь­ко с 1934, ко­гда Дж. И. Тей­лор, Э. Оро­ван и М. По­ля­ни впер­вые объ­яс­ни­ли атом­ный ме­ха­низм пла­стич­но­сти кри­стал­лов как про­цесс пе­ре­ме­ще­ния Д. (см.

Пла­стич­ность кри­стал­лов).

Про­стей­ши­ми ви­да­ми Д. яв­ля­ют­ся крае­вая и вин­то­вая Д. (рис.). Крае­вая Д. пред­став­ля­ет со­бой ли­нию, вдоль кото­рой внут­ри кри­стал­ла об­ры­ва­ет­ся «лиш­няя» атом­ная по­лу­плос­кость. Та­кая Д. мо­жет быть по­лу­че­на в ре­зуль­та­те не­пол­но­го сдви­га верх­ней час­ти кри­стал­ла на один пе­ри­од кри­стал­лич.

ре­шёт­ки вдоль плос­ко­сти, про­хо­дя­щей че­рез ось Д. На­прав­ле­ние сдви­га и его ве­ли­чи­на оп­ре­де­ля­ют осн. ха­рак­те­ри­сти­ку Д. – т. н. век­тор Бюр­гер­са, ко­то­рый по­стоя­нен вдоль всей ли­нии Д. и не­ред­ко на­зы­ва­ет­ся её то­по­ло­гич. за­ря­дом. Ес­ли сдвиг не пер­пен­ди­ку­ля­рен, а па­рал­ле­лен оси Д., то Д.

на­зы­ва­ет­ся вин­то­вой. В этом слу­чае ни од­на из атом­ных плос­ко­стей не об­ры­ва­ет­ся внут­ри кри­стал­ла, но все они смы­ка­ют­ся в еди­ную вин­то­вую по­верх­ность. В мес­те вы­хо­да вин­то­вой Д. на внеш­нюю по­верх­ность кри­стал­ла об­ра­зу­ет­ся сту­пень­ка. Лёг­кость при­сое­ди­не­ния но­вых ато­мов к та­кой сту­пень­ке обу­слов­ли­ва­ет т.

 н. спи­раль­ный ме­ха­низм ус­ко­рен­но­го рос­та кри­стал­лов. Кро­ме чис­то крае­вых и вин­то­вых Д. воз­мож­ны бо­лее об­щие ком­би­ни­ро­ван­ные ти­пы кри­во­ли­ней­ных Д. Ли­нии Д. не мо­гут об­ры­вать­ся внут­ри кри­стал­ла, они долж­ны ли­бо за­мы­кать­ся в пет­ли, ли­бо раз­ветв­лять­ся на Д. с др.

век­то­ра­ми Бюр­гер­са (но с той же их сум­мой), ли­бо вы­хо­дить на по­верх­ность кри­стал­ла.

При­ме­не­ние элек­трон­ных мик­ро­ско­пов с боль­шой раз­ре­шаю­щей спо­соб­но­стью по­зво­ля­ет не­по­сред­ст­вен­но на­блю­дать на­ру­ше­ния в рас­по­ло­же­нии атом­ных сло­ёв. Ис­ка­же­ние кри­стал­лич. струк­ту­ры вбли­зи Д. (т. н. яд­ро Д.) ох­ва­ты­ва­ет об­ласть диа­мет­ром в неск.

пе­рио­дов кри­стал­лич. ре­шёт­ки. За пре­де­ла­ми яд­ра кри­стал­лич. ре­шёт­ка яв­ля­ет­ся ло­каль­но де­фор­ми­ро­ван­ной, но то­по­ло­ги­че­ски со­вер­шен­ной. Ве­ли­чи­на этих де­фор­ма­ций и со­пут­ст­вую­щих им даль­но­дей­ст­вую­щих внутр.

уп­ру­гих на­пря­же­ний в кри­стал­ле убы­ва­ет об­рат­но про­пор­цио­наль­но рас­стоя­нию от Д. При­ло­жен­ная из­вне на­груз­ка, взаи­мо­дей­ст­вуя с по­лем внутр. на­пря­же­ний, мо­жет при­во­дить к дви­же­нию Д. Пе­ре­ме­ще­ние Д.

на за­мет­ные рас­стоя­ния при­во­дит к не­об­ра­ти­мой (в от­ли­чие от уп­ру­гой де­фор­ма­ции) пла­сти­че­ской де­фор­ма­ции кри­стал­ла.

Раз­ли­ча­ют кон­сер­ва­тив­ные (без пе­ре­но­са мас­сы) и не­кон­сер­ва­тив­ные дви­же­ния Д. По­след­ний тип дви­же­ния воз­мо­жен прак­ти­че­ски вдоль лю­бо­го на­прав­ле­ния (напр., под ост­рым уг­лом к экс­т­ра­плос­ко­сти крае­вой Д.

), но тре­бу­ет по­вы­шен­ных тем­пе­ра­тур, по­сколь­ку дол­жен со­про­во­ж­дать­ся диф­фу­зи­он­ны­ми по­то­ка­ми то­чеч­ных де­фек­тов (ва­кан­сий или ме­жу­зель­ных ато­мов). При уме­рен­ных тем­пе­ра­ту­рах реа­ли­зу­ет­ся лишь кон­сер­ва­тив­ный тип дви­же­ния пу­тём пе­ре­со­еди­не­ния свя­зей в яд­ре Д.

Это воз­мож­но лишь в вы­де­лен­ных плос­ко­стях, на­зы­вае­мых плос­ко­стя­ми сколь­же­ния и за­да­вае­мых со­во­куп­но­стью на­прав­ле­ний век­то­ра Бюр­гер­са и ли­нии дис­ло­ка­ции.

При сме­ще­нии Д. в плос­ко­сти сколь­же­ния на пе­ри­од кри­стал­лич. ре­шёт­ки про­ис­хо­дят раз­рыв атом­ных свя­зей в дис­ло­ка­ци­он­ном яд­ре и пе­ре­со­еди­не­ние их в но­вом по­ло­же­нии, эк­ви­ва­лент­ном ис­ход­но­му, вслед­ст­вие пе­рио­дич­но­сти кри­стал­ла. Под­виж­ность Д.

за­ви­сит от ха­рак­те­ра сил меж­атом­ных свя­зей, раз­ры­вае­мых при пе­ре­ме­ще­нии Д., от взаи­мо­дей­ст­вия с при­мес­ны­ми ато­ма­ми и др. де­фек­та­ми кри­стал­ла, а так­же с фо­но­на­ми и элек­тро­на­ми про­во­ди­мо­сти. На­пря­же­ния, тре­буе­мые для во­вле­че­ния Д.

в дви­же­ние по плос­ко­сти сколь­же­ния, зна­чи­тель­но мень­ше, чем для сдви­га час­ти кри­стал­ла как це­ло­го вдоль этой плос­ко­сти при от­сут­ст­вии Д. Раз­ни­ца за­клю­ча­ет­ся в не­со­пос­та­ви­мом ко­ли­че­ст­ве раз­ры­вае­мых свя­зей, чем и объ­яс­ня­ет­ся пла­стич­ность мн.

ре­аль­ных ме­тал­лов, со­дер­жа­щих боль­шое ко­ли­че­ст­во дис­ло­ка­ций.

Обыч­но Д. воз­ни­ка­ют уже в про­цес­се рос­та кри­стал­ла. Вы­ра­щи­ва­ние без­дис­ло­ка­ци­он­ных или ма­ло­дис­ло­ка­ци­он­ных кри­стал­лов пред­став­ля­ет со­бой слож­ную тех­но­ло­гич.

за­да­чу, ус­пеш­но ре­шае­мую в по­лу­про­вод­ни­ко­вой пром-сти, обес­пе­чи­ваю­щей про­из-во тран­зи­сто­ров, ком­пь­ю­тер­ных чи­пов и т. п. В не­ко­то­рых др. про­из­вод­ст­вах, на­про­тив, на­ли­чие оп­ре­де­лён­ной плот­но­сти дис­ло­ка­ций по­лез­но для об­ра­бот­ки ма­те­риа­лов (т. к.

при­да­вае­мая дис­ло­ка­ция­ми пла­стич­ность пре­до­хра­ня­ет ма­те­риа­лы от хруп­ко­го раз­ру­ше­ния при из­го­тов­ле­нии из­де­лий). При при­ло­же­нии к кри­стал­лу на­груз­ки Д.

на­чи­на­ют раз­мно­жать­ся, при­чём при пре­вы­ше­нии не­ко­то­ро­го по­ро­го­во­го зна­че­ния на­груз­ки, на­зы­вае­мо­го пре­де­лом те­ку­че­сти, раз­мно­же­ние Д. при­об­ре­та­ет мас­со­вый ха­рак­тер и на­чи­на­ет­ся пла­стич. те­че­ние ма­те­риа­ла.

По­сколь­ку по­вы­ше­ние темп-ры спо­соб­ст­ву­ет пре­одо­ле­нию барь­е­ров на пу­ти дви­же­ния Д., пре­дел те­ку­че­сти, как пра­ви­ло, по­ни­жа­ет­ся при на­гре­ва­нии кри­стал­ла. Это свой­ст­во из­дав­на ис­поль­зу­ет­ся для об­лег­че­ния об­ра­бот­ки ма­те­риа­лов, тре­бую­щей из­ме­не­ния их фор­мы.

Д. влия­ют не толь­ко на ме­ха­нич. свой­ст­ва кри­стал­лич. ма­те­риа­лов, та­кие как проч­ность и пла­стич­ность, но и на мн. дру­гие фун­дам. свой­ст­ва твёр­дых тел. Воз­ник­но­ве­ние обор­ван­ных атом­ных свя­зей в яд­ре Д.

мо­жет вес­ти к за­хва­ту элек­тро­нов и свя­зан­но­му с этим влия­нию Д. на элек­трич. со­про­тив­ле­ние, лю­ми­нес­цент­ные и маг­нит­ные свой­ст­ва ма­те­риа­ла. Ско­рость диф­фу­зи­он­но­го пе­ре­ме­ще­ния то­чеч­ных де­фек­тов вдоль оси Д.

(«тру­боч­ная диф­фу­зия»), как пра­ви­ло, вы­ше, чем в объ­ё­ме со­вер­шен­но­го кри­стал­ла. По­это­му Д. спо­соб­ст­ву­ют ус­ко­ре­нию диф­фу­зи­он­ных про­цес­сов и ис­поль­зу­ют­ся для вы­ве­де­ния из кри­стал­лов вред­ных при­ме­сей.

Спо­соб­ность во­вле­кае­мых в ко­ле­ба­тель­ное дви­же­ние Д. рас­сеи­вать ме­ха­нич. энер­гию при­во­дит к за­мет­но­му вкла­ду во внут­рен­нее тре­ние в твёр­дых те­лах.

Понятие о теории дислокации

• Все реальные кристаллические твердые тела (в частности, металлы) имеют большее или меньшее количество дефектов кристаллической структуры, оказывающих влияние, нередко решающее, на макро­скопические свойства твердых тел.
• •Такими дефектами являются:
• точечные дефекты — вакансии {узлы кристаллических решеток, незаполненные атомами), межузель­ные атомы и др.
• одномерные (линейные) дефекты — дислокации-,
• двумерные (поверхностные) де­фекты — границы зерен и двойников, дефекты упаковки и др.;
• Успехи учения о прочности и пластичности материалов связаны с развитием представлений о роли де­фектов структуры при пластической деформации и разрушении кристал­лических твердых тел.
• Дислокациями называют линейные несовершенства или одномерные де­фекты кристаллических решеток ре­альных металлов, представляю­щие собой особые нарушения кристаллического строения, связанные с отклонениями реальных кристаллов от идеального их строения.

Дислокации бывают краевые, винтовые и смешанные криволиней­ные. Возникают они в металлах в процессе кристаллизации, пласти­ческой деформации и по другим причинам, вызывающим создание полей напряжений в кристаллической решетке, приводящих к соот­ветствующим локальным деформациям и смещениям.

Теория дислокаций позволила объяснить, почему реальная проч­ность металлов [для технически чистого железа ав = 2,5—3,0 МН/’м3 (МПа)] разительно отличается от теоретической прочности (под­считанной с учетом сил межатомного взаимодействия), которая для железа составляет около 200 МН/ма (МПа)[6].

Представим себе, что в кристаллической решетке по каким-либо причинам появилась лишняя полуплоскость атомов, так называемая экстраплоскость Q (рис. 21). Край 3—3′ такой плоскости образует линейный дефект (несовершенство) решетки, который называют крае­

вой дислокацией. Если такая дислокация находится вверху, то ее счи­тают положительной и обозначают знаком Т; краевую дислокацию, находящуюся внизу (отрицательную), обозначают знаком_Д.

Краевая дислокация может прос­тираться в длину на многие тысячи периодов решетки, ее линия не мо­жет быть прямой и, обладая поверх­ностным натяжением, она стре­мится замкнуться в контур. Вокруг дислокации возникает зона упру­гого искажения решетки. Ширина дислокаций, т, е. расстояние от цент­ра дефекта до места решетки без искажения, невелика и равна нес­кольким межатомным расстояниям.

Вследствие искажения решетки в районе дислокации последняя лег­ко может смещаться вправо или влево от нейтрального положения и устанавливать связь краевых своих атомов 3 с атомами 1 (см. рис.

21), а соседняя справа (слева) Полуплос­кость будет при этом переходить в промежуточное положение, превра­щаясь тем самым в экстраплоскость и образуя дислокацию вдоль краевых атомов 2 и т. д.

Таким образом, дис­локация может перемещаться (вернее —- передаваться как эстафета) вдоль некоторой плоскости скольжения, расположенной перпендикулярно к экстраплоскости Q.

Дислокации в металлах можно наблюдать с помощью электронного микроскопа.

Для отожженных металлов плот­ность дислокаций (pD), т. е. коли­чество дислокаций, пересекающих каждый см2, составляет 107—10*, а для сильно наклепанных — 10to— 10“

Теоретически, при элементарном пластическом сдвиге (рис. 22), если учесть силы межатомного вза­имодействия для каждой пары со­пряженных атомов (относительно плоскости скольжения А А) 1-І’, 2—2′ и т. д. и учитывая, что в плоскости скольжения реального метал­лического кристалла имеется около 1014 атомов на каждый см2 сече­ния, требуется чрезвычайно большое усилие (для технического желе­

за, как уже отмечалось, в десятки раз большее, чем это реально наблю­дается).

Согласно дислокационной теории пластический сдвиг в металле стедует рассматривать как процесс эстафетного перемещения дисло­каций. Упрощенная схема этого процесса представлена на рис. 23-

Рис. 23. Дислокационная схема пластического сдвига: а. 0. в. г. — фазы сдвига

В результате наличия дислокации (рис. 23, о) в кристалле по обе стороны скольжения А А возникает искаженное состояние кристал­лической решетки с нарушением порядка идеальных связей между ато­мами. В этом случае достаточно будет приложить небольшое внешнее усилие Р (значительно меньше силы Р для идеальной решетки — рис.

23, б), чтобы вызвать распространение волны последовательных частных смещений вертикальных рядов атомов над плоскостью сколь­жения АА, не превосходящих по величине одного межатомного рас­стояния.

В результате прохождения этой волны дислокация, как своеобразная эстафета, будет последовательно передаваться рядам атомов 3, 4… и в некоторый момент займет положение, представлен­ное на рис. 23, в. В итоге же передачи движения от частного смещения ряда атомов I дислокация выйдет на поверхность и исчезнет, как это показано на рис. 23, г.

Итак, конечным результатом перемещения дислокации вдоль плоскости скольжения АА явился сдвиг на одно межатомное расстояние, причем для осуществления этого сдвига понадобилось значительно меньшее усилие, чем при отсутствии дис­локации.

Отсюда можно сделать вывод, что процесс сдвига в кристалле про­исходит тем легче, чем больше дислокаций имеется в металле. Наобо — 3—545

рот, чем меньше в металле таких дислокаций, тем меньше возмож­ностей для сдвига и тем прочнее металл. В металле, в котором не обра­зуются дислокации, сдвиг возможен только за счет одновременного смещения (как целого) одной части кристалла относительно другой.

В этом случае прочность бездислокационного металла должна быть

равна теоретической (точка I на рис. 24).

Прочность нитевидных метал­лических кристаллов — так назы­ваемых усов (точка 2 на рис. 24) — оказалась ближе к теоретичес­кой, что, согласно, предположени­ям, обусловлено весьма малым количеством дислокаций. Так, например, для нитевидных крис­таллов железа предел прочности на разрыв составляет о„ =140 МН/м2 (МПа).

Большое повышение прочности металла с увеличением совершенст­ва его кристаллического строения (на примере нитевидных кристал­лов) является убедительным под­тверждением теории дислокации.

Кроме получения бездислока — ционных металлических кристал­лов существует другой путь уп­рочнения металлов. Оказывается, что реальная прочность металлов падает с увеличением числа дисло­каций только вначале. Достигнув минимального значения при некоторой критической плотности дислокаций (р1ф на рис. 24), реальная прочность вновь начинает возрастать.

Повышение реальной прочности с возрастанием плотности дислокаций выше ркр объясняется тем, что при этом возникают не только параллельные друг другу дислокации, но и дислокации в раз­ных плоскостях и направлениях. Такие дислокации будут мешать друг другу перемещаться, т. е.

в элементарный акт пластической де­формации будет вовлекаться одновременно все большее число атомов, и реальная прочность металла повысится.

Традиционными способами упрочнения металлов, ведущими к увеличению плотности дислокаций, являются механический наклеп, измельчение зерна и общее фрагментирование кристаллов в результате термообработки.

Некоторые давно известные методы легирования (например, внесение в решетку основного металла чужеродных ато­мов), создающие всякого рода несовершенства и искажения кристал­лической решетки, препятствуют свободному перемещению дислока­ций или блокируют их. Сюда же относятся способы образования ее

структур с так называемыми упрочняющими фазами (например, дис­персионное твердение).

Однако во всех этих случаях упрочнение далеко не достигает тео­ретического значения. Следовательно, в той или иной степени наличие дислокаций в реальном металлическом кристалле является причиной понижения его прочности за счет проявления способности пластиче­ски деформироваться при напряжениях, меньших теоретического уровня.

Следует отметить, что взаимодействия дислокаций друг с другом и с другими дефектами металла настолько сложны, что на основе прос­тых дислокационных теорий нельзя предсказывать прочность твердых тел. Однако теория дислокаций позволяет качественно характери­зовать процессы деформации, разрушения и упрочнения твер­дых тел.

Теория дислокаций на сегодняшний день стала неотъемлемой частью физики твердого тела и физического металловедения.

Все процессы, протекающие в металлах и сплавах, а также форми­рование их свойств неразрывно связаны с характером и плотностью дефектов кристаллического строения и, в первую очередь, дислокаций. Так, пластическая деформация, обычно представляющая собой внутри — зеренный сдвиг, осуществляется, как об этом было сказано выше, путем движения дислокаций.

Теория дислокаций объясняет зависимость между деформациями и напряжениями, вскрывает причины деформационного упрочнения (наклепа). Чем больше плотность дислокаций при р а в н о м е р — ном их распределении, тем выше прочность металла.

Упрочнение твердых растворов нельзя объяснить без учета взаимодействия растворенных атомов с дефектами кристал­лического строения и, в первую очередь, с дислокациями.

Вокруг дислокаций могут создаваться скопления чужеродных атомов, получивших название «атмосфер Котрелла». Образование таких скоплений (особенно внедренными атомами) может в значитель­ной степени затруднять движение дислокаций увеличивая тем самым сопротивление пластической деформации.

Процесс разрушения металлов невозможно объ­яснить, не основываясь на теории дислокаций, поскольку разруше­ние и пластическая деформация неразрывно связаны между собой. Предложены различные дислокационные модели образования зароды­шей треищн, возникающих благодаря скоплению дислокаций перед барьерами.

Не привлекая теорию дислокаций, нельзя объяснить ползучесть металлов, поскольку она определяется процессами скольжения и «переползания» дислокаций.

Дислокации оказывают существенное влияние на процесс диффузии. Так как дислокации могут быть источником вакансий (атомных дырок в кристаллической решетке), то они способствуют ускорению диффу­зионных процессов. Дислокации могут уменьшать работу образова­ния зародышей новой фазы, являясь областями преимущественного ее выделения (например, при дисперсионном твердении).

Теория дислокаций описывает характер взаимодействия дислока — ций с дисперсными частицами других фаз и вскрывает причины упрочнения стареющих сплавов.,

Итак, многие вопросы металловедения неразрывно связаны с тео­рией дислокаций. Теория дислокаций подсказала пути реализации скрытых резервов прочности металлов, заключающиеся в более пол­ном использовании сил межатомных связей в кристаллической решет­ке.

Это выразилось, в частности, в разработке принципиально новых, практически бездислокационных материалов — нитевидных кристал­лов металлов и других кристаллических веществ (графита, окислов и др.

), обладающих чрезвычайно высокой прочностью в повышении прочности ранее известных марок стали путем комбинированной тер­момеханической обработки (ТАЮ).

Дислокационная теория служит дальнейшему развитию металло­ведения и его практического приложения.