- Электронная проводимость металлов
- 1.12. Электрический ток в металлах
- Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Видемана-Франца
- Основные положения и опытное обоснование классической электронной теории электропроводности металлов
- Классическая электронная теория проводимости Друде-Лоренца
- Формула Друде
- Опыт Толмена и Стюарта
Как вы знаете, электрический ток могут проводить и твердые, и жидкие, и газообразные тела. На практике, чаще всего применяются металлические проводники. Можно привести много примеров: линии электропередач, обеспечивающие передачу энергии от различных источников тока к потребителям.
Генераторы, электронагревательные приборы и так далее. Как мы уже говорили ранее, хорошими проводниками являются некоторые растворы. Наиболее распространенный пример — это батарейка, в которой используется электролит. Примеров использования батарей и аккумуляторов тоже достаточно: они используются в автомобилях, ноутбуках, мобильных телефонах, планшетах и так далее.
Напомним, что помимо проводников, существуют такие тела, как полупроводники и диэлектрики. Как вы знаете, диэлектрики используются для изоляции проводки или электроприборов. Полупроводники представляют довольно большой интерес, поскольку их проводимостью достаточно легко управлять, а это открывает большие возможности.
Со всем выше перечисленным мы познакомимся по окончании курса физики десятого класса, и начнем с проводимости металлов.
Мы уже много раз говорили, что электрический ток — это упорядоченное движение заряженных частиц, и всегда утверждали, что в металлах носителями свободных зарядов являются электроны. Дело в том, что за этим утверждением стоят многочисленные опыты разных ученых. Мы рассмотрим несколько таких опытов.
В 1901 году, Эдуард Рикке провел следующий эксперимент: он подключил к электрической цепи металлические цилиндры, плотно прилегающие друг к другу. В центре находился алюминиевый цилиндр, а по краям — медные.
В течение приблизительно одного года через эти цилиндры протекал электрический ток. После окончания эксперимента, все три цилиндра были исследованы на предмет изменения химического состава.
Выяснилось, что никаких изменений не произошло, за исключением очень незначительной диффузии. Это послужило доказательством того, что ток в металлах обусловлен именно движением электронов.
Если бы в движении участвовали какие-то другие частицы (например, ионы кристаллической решетки), то это, неизбежно привело бы к изменению химического состава.
Другой опыт, был проведен в 1912 году учеными Леонидом Мандельштамом и Николаем Папалекси. К катушке, которая могла вращаться вокруг своей оси, был подключен гальванометр при помощи скользящих контактов.
При резкой остановке катушки, гальванометр регистрировал кратковременные токи. Дело в том, что при резкой остановке заряженные частицы какое-то время могли двигаться по инерции относительно проводника (то есть проволоки катушки).
Поскольку сила тока характеризуется зарядом, а инерция — массой частиц, переносимый при торможении заряд пропорционален отношению заряда частиц к их массе.
Из этого эксперимента было определено это соотношение, которое совпало с найденным до этого из других опытов отношением модуля заряда электрона к его массе:
Таким образом, эксперимент Мандельштама и Папалекси еще раз подтвердил, что ток в металлах обусловлен движением электронов. Поэтому, проводимость металлов называют электронной проводимостью.
Вы уже знаете, что электроны в металлах двигаются с постоянной скоростью из-за того, что взаимодействуют с ионами кристаллической решетки. Это приводит к тому, что скорость движения электронов пропорциональна напряженности электрического поля:
В свою очередь, напряженность пропорциональна напряжению. Из чего мы можем заключить, что скорость электронов в проводнике пропорциональна напряжению на концах этого проводника:
Напомним, что не так давно мы выяснили, что скорость также пропорциональна и силе тока:
Из этого мы можем сделать вывод, что ???? ~ ????, а это подтверждает закон Ома.
Теперь, когда мы выяснили, что электрический ток в металлах действительно обусловлен движением электронов, следует обратить внимание на одно из следствий этого явления.
Электроны взаимодействуют с ионами кристаллической решетки и, тем самым нагревают проводник. Но, чем больше проводник нагревается, тем более интенсивными становятся колебания частиц проводника и тем больше они мешают движению электронов.
Следовательно, в металлах существует определенная зависимость их электрического сопротивления от температуры.
Экспериментально была установлена зависимость сопротивления от температуры:
В формуле мы видим коэффициент пропорциональности α, который называется температурным коэффициентом сопротивления. Мы можем немного преобразовать выражение, описывающее зависимость сопротивления от температуры, чтобы дать определение температурному коэффициенту сопротивления:
Итак, температурный коэффициент сопротивления численно равен относительному изменению сопротивления при нагревании на 1 оС. Под относительным изменением сопротивления понимается отношение изменения сопротивления к конечному сопротивлению. Поскольку мы выяснили, что у металлов сопротивление увеличивается с увеличением температуры, можно сделать вывод, что для всех металлов коэффициент α > 0.
- Вспомним, что сопротивление проводника зависит от трех величин: удельное сопротивление материала, из которого сделан проводник, площадь поперечного сечения проводника и его длина:
- Поскольку геометрические размеры проводника при нагревании меняются ничтожно мало, можно сделать вывод, что изменяется удельное сопротивление:
- Из полученной формулы можно сделать вывод, что удельное сопротивление металлов линейно зависит от температуры.
Эта зависимость используется в так называемых термометрах сопротивления. Термометр сопротивления представляет собой проводник, зависимость сопротивления которого от температуры хорошо известна.
Чаще всего используют платиновую проволоку. Измеряя ее сопротивление можно судить о температуре.
Преимущество подобного термометра заключается в том, что он пригоден для измерения температур в значительно более широком диапазоне, чем это возможно, используя жидкостные термометры.
Возникает вопрос: а что будет происходить при очень низких температурах? Этим вопросом еще в 1911 году задался Хейке Камерлинг-Оннес. В качестве опыта, он поместил ртуть в жидкий гелий и наблюдал, как постепенно уменьшается удельное сопротивление с падением температуры.
Однако, когда температура опустилась до четырех целых одной десятой кельвина, сопротивление резко упало до нуля. Такое явление получило название сверхпроводимости, а температура, при которой наступает это состояние, была названа критической температурой.
Явление сверхпроводимости возникает во многих металлах при достаточно низких температурах (около 25 К). Это явление можно объяснить тем, что при таких низких температурах беспорядочное движение электронов становится очень незначительным. Иными словами, они двигаются, не соударяясь с ионами кристаллической решетки, таким образом, не замедляя своего движения и не нагревая проводник.
Конечно, это объяснение существенно упрощено, но оно дает общее представление о том, как возникает явление сверхпроводимости. Тот факт, что в состоянии сверхпроводимости проводники не нагреваются, открывает большие перспективы.
Если найти способ создать явление сверхпроводимости при обычных (комнатных) температурах, то можно было бы передавать электроэнергию по проводам без всяких потерь.
Сверхпроводимость используется для создания электромагнитов, которые могут создавать магнитное поле в течение длительного времени без всяких потерь энергии.
Также, сверхпроводящие магниты используются в ускорителях элементарных частиц (таких как Большой Адронный Коллайдер). В 1986 году удалось создать некоторые соединения, переходящие в состояние сверхпроводимости при температурах около 100 К.
На сегодняшний день, нет известных соединений, в которых бы наблюдалась сверхпроводимость при температуре выше 138 К (при нормальном давлении).
Рассмотрим еще один интереснейший эффект явления сверхпроводимости, который получил название эффекта Мейснера. Поместим два керамических цилиндра в специальную емкость и зафиксируем их.
При температуре 93 К эти цилиндры становятся сверхпроводящими. Для охлаждения можно использовать жидкий азот. Если теперь поднести к цилиндрам достаточно сильный магнит, то он зависнет над ними. Как вы знаете из курса физики девятого класса, при изменении магнитного потока через контур, возникает индукционный ток.
В обычных условиях, этот ток был бы незначительным и кратковременным. Однако, в состоянии сверхпроводимости, сопротивление равно нулю, поэтому, ток продолжает течь по цилиндрам. Этот ток создает магнитное поле, которое и вызывает силы отталкивания между цилиндрами и магнитом.
Если же теперь мы поместим над цилиндрами магнит в виде колесика и раскрутим его, то он будет продолжать крутиться до тех пор, пока цилиндры находятся в состоянии сверхпроводимости. Заметим, что магнит крутится, не касаясь цилиндров и не нагреваясь, то есть никаких потерь энергии не происходит.
Тем не менее, нет возможности получить сколь угодно большой ток в сверхпроводниках, поскольку определенное критическое значение силы тока разрушает состояние сверхпроводимости.
Однако, конструкции, основанные на подобном принципе, могли бы существенно усовершенствовать электродвигатели и генераторы, значительно упростить устройства для аккумулирования энергии и многое другое. Поэтому, сегодня получение сверхпроводимости при комнатных температурах является одной из очень важных задач в физике.
Электронная проводимость металлов


Средняя оценка: 4.7
Всего получено оценок: 114.
Обновлено 7 Сентября, 2020
Средняя оценка: 4.7
Всего получено оценок: 114.
Обновлено 7 Сентября, 2020
В 10 классе известно, что вещество, являющееся проводником, должно содержать много высокоподвижных носителей электрического заряда. Наилучшими проводниками в нормальных условиях являются металлы. Кратко рассмотрим механизм электронной проводимости металлов.
Вещества, обладающие металлической проводимостью, как правило, имеют во внешней электронной оболочке малое количество электронов, которые относительно слабо связаны ядром и внутренними электронными оболочками. Это и определяет особенности металлической кристаллической решетки.
В кристалле металла ионы с внутренними электронными оболочками образуют узлы решетки, как и в любом другом кристалле.
А электронные облака внешних валентных электронов перекрывают друг друга так, что они оказываются общими не только для двух ионов (как это бывает в ковалентной связи), а сразу для нескольких ионов.
В результате электроны могут свободно перемещаться между всеми этими ионами, попадая в поле действия более далеких ионов, и перемещаясь уже между ними.
То есть, электроны в кристаллической решетке металла движутся не строго по орбитам между соседними атомами (как в ковалентном кристалле), а образуют своего рода «электронный газ», распределенный по всему кристаллу.
Рис. 1. строение металлической кристаллической решетки.
Такое строение кристаллической решетки приводит к тому, что электроны очень легко способны перемещаться под действием внешнего электрического поля. То есть, металлы, имеют много свободных легких электронов и обладают большой проводимостью.
Доказательством существования свободных электронов явились опыты, проведенные в 1916г Т. Стюартом и Р.Толменом (позже выяснилось, что такие же опыты ставились и ранее Л. Мандельштамом и Н.Папалекси, но результат их не был опубликован).
Идея этих опытов состоит в том, что если внутри металла существуют свободные электроны, то при движении кристаллической решетки с ускорением электроны должны «отставать» от ионов. В результате на разных концах кристалла концентрация электронов должна быть разной, и порождать разность потенциалов.
Для опыта использовалась катушка, к которой был подключен чувствительный телефонный капсюль. Когда катушка колебалась вокруг продольной оси, в ней возникала электроинерционная разность потенциалов, и капсюль издавал звук.
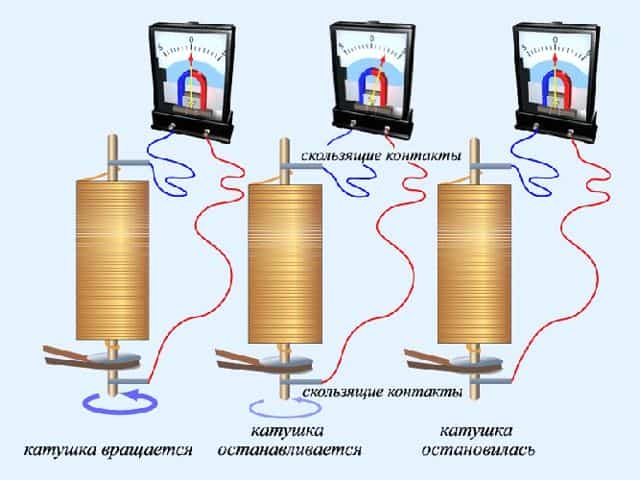 Рис. 2. Опыт Мандельштама и Папалекси.
Рис. 2. Опыт Мандельштама и Папалекси.
В 1900г П.Друде, основываясь на положениях молекулярно-кинетической теории, и рассматривая электроны в металле, как идеальный газ, создал классическую электронную теорию проводимости металлов. Первоначально эта теория не учитывала распределение скоростей электронов, учет этого распределения был выполнен в 1904г Х.Лоренцем.
Теория Друде-Лоренца смогла объяснить законы Ома, Джоуля-Ленца, механизм проводимости и зависимости сопротивления от температуры.
Однако, со временем стало появляться все больше данных, необъяснимых в рамках классичепской теории. В частности, имелись расхождения по температурному коэффициенту сопротивления, по значениям теплоемкости.
И уж совсем необъяснимым было явление сверхпродоимости, открытое в 1911г.
Все эти расхождения имеют квантовый характер, и поэтому объясняются в рамках более совершенной квантовой теории проводимости твердых тел (зонной теории проводимости).
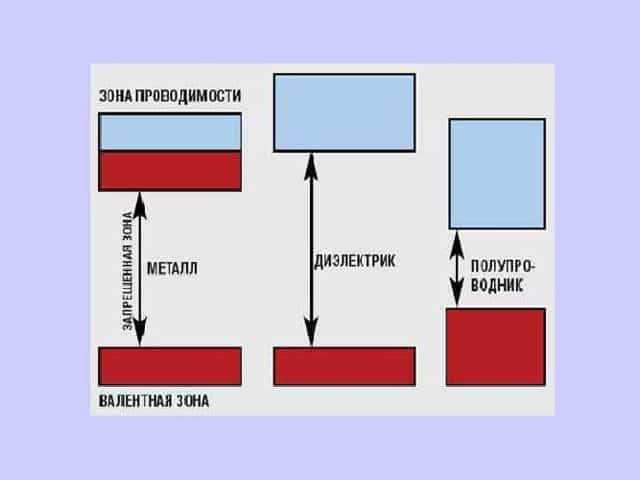 Рис. 3. Зонная теория проводимости.
Рис. 3. Зонная теория проводимости.
Высокая проводимость металлов обуславливается особенностями кристаллической решетки, в которой электронные облака соседних атомов сильно перекрываются друг с другом, поэтому электроны могут легко перемещаться между атомами, обеспечивая низкое электрическое сопротивление. Первоначально была разработана классическая теория проводимости Друде-Лоренца. В настоящее время она сменилась зонной теорией проводимости.
Чтобы попасть сюда — пройдите тест.
Средняя оценка: 4.7
Всего получено оценок: 114.
А какая ваша оценка?
Гость завершил
Тест «Отцы и дети»с результатом 9/15
Гость завершил
Тест Дроби (5 класс)с результатом 10/10
Гость завершил
Тест «Отцы и дети»с результатом 13/15
Гость завершил
Тест Запятыес результатом 8/10
Гость завершил
Тест «Косцы»с результатом 4/8
Гость завершил
Тест «Судьба человека»с результатом 10/12
Не подошло? Напиши в х, чего не хватает!
1.12. Электрический ток в металлах
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси.
В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.
Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси.
Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда.
Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.
| Рисунок 1.12.1.Схема опыта Толмена и Стюарта |
- При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью Eст поля сторонних сил:
- Следовательно, в цепи при торможении катушки возникает электродвижущая сила , равная
где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный
- Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки.
- Отсюда удельный заряд e / m свободных носителей тока в металлах равен:
Все величины, входящие в правую часть этого соотношения, можно измерить.
На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.
По современным данным модуль заряда электрона (элементарный заряд) равен а его удельный заряд есть
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов.
Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ.
Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).
| Рисунок 1.12.2.Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов |
Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.
Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.
Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки.
В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа.
Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 105 м/с.
При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме
Число таких электронов равно где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует: или
Концентрация n атомов в металлах находится в пределах 1028–1029 м–3.
Оценка по этой формуле для металлического проводника сечением 1 мм2, по которому течет ток 10 А, дает для средней скорости упорядоченного движения электронов значение в пределах 0,6–6 мм/c.
Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения Рис. 1.12.
3 дает представление о характере движения свободного электрона в кристаллической решетке.
| Рисунок 1.12.3.Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа сильно преувеличены |
Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·108 м/с.
Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона.
В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям.
Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.
Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.
Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение Поэтому к концу свободного пробега дрейфовая скорость электрона равна где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа равно половине максимального значения:
Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде:
где U = El – напряжение на концах проводника.
Полученная формула выражает закон Ома для металлического проводника.
Электрическое сопротивление проводника равно:
а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:
Закон Джоуля–Ленца. К концу свободного пробега электроны под действием поля приобретают кинетическую энергию
Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.
За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:
Это соотношение выражает закон Джоуля–Ленца.
Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.
Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.
Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение в то время как из эксперимента получается зависимость ρ ~ T. Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость.
Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах.
При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х.
Каммерлинг-Оннесом в 1911 году. При некоторой определенной температуре Tкр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К.
Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni3Sn) имеет критическую температуру 18 К.
Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.
| Рисунок 1.12.4.Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник |
Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.
Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.
Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения Tкр = 35 K.
Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью.
В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.
В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями Tкр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.
Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
|
Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Видемана-Франца
Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Видемана-Франца.
Электрический ток в металлах –это упорядоченное движение электронов под действием электрического поля.
Это предположение было экспериментально подтверждено в опыте К. Рикке (1911).
Через цепь из трех последовательных цилиндров — медного, алюминиевого и снова медного — в течение долгого времени (около года) пропускался электрический ток — в общей сложности через цилиндры прошел заряд 3,5 МКл.
Однако никаких следов переноса вещества ( меди или алюминия) не было обнаружено.
Отсюда следовало, что электропроводность металлов отвечают свободные заряды, общие для всех металлов — на эту роль подходили только электроны.
Еще одно убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыт Толмена и Стьюарта)(1916).
Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру. Раскрученная катушка резко тормозилась, и
в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся гальванометром.
При торможении вращающейся катушки на каждый носитель заряда e массой m действует тормозящая сила, которая играет роль сторонней силы, т. е. силы неэлектрического происхождения:
Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью поля сторонних сил:
Следовательно, в цепи при торможении катушки возникает электродвижущая сила:
За время торможения катушки по цепи протечет заряд q, равный:
где – длина проволоки катушки, I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, – начальная линейная скорость проволоки.
Полученное в опытах значение удельного заряда носителей тока в металле оказался близким к удельному заряду электрона
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П.
Друде на основе гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории.
Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ.
Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла. Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода.
При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории:
При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток.
Величина дрейфовой скорости электронов лежит в пределах 0,6 – 6 мм/c.
Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения.
Малая скорость дрейфа не противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·108 м/с. Через время (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона.
В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям.
Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.
- Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках: закон Ома, закон Джоуля – Ленца и объясняет существование электрического сопротивления металлов.
- Закон Ома:
- Электрическое сопротивление проводника:
- Закон Джоуля–Ленца:
- Немецкие физики Видеман и Франц на основе экспериментов установили (закон Видемана — Франца) (1853), что для всех металлов при одной и той же температуре отношение теплопроводности К к удельной электрической проводимости g одинаково:
- Позже (1888 г.) Лоренц показал, что отношение пропорционально абсолютной температуре Т:
Электронная теория металлов позволила получить этот закон и вычислить значение константы С, основываясь на предположении, что теплопроводность металлов в основном осуществляется электронами проводимости, т.е. электронным газом.
Теплопроводность газа
Где C1=3k2/e2 C1=2.23*10-8 Дж2/(Кл*К)2
Эта величина оказалась лишь ненамного меньше значения, найденного из опытов.
Основные положения и опытное обоснование классической электронной теории электропроводности металлов
| Заказать ✍️ написание работы |
Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла.
Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде (1863—1906) и разработанной впоследствии нидерландским физиком X.
Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории.
Первый из таких опытов — опыт Рикке(1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндров (Сu, Аl, Сu) одинакового радиуса.
Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (»3,5•106 Кл), никаких, даже микроскопических, следов переноса вещества не обнаружилось.
Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856—1940) электроны.
Для доказательства этого предположения необходимо было определить знак и величину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед, как
смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат советским физикам С. Л.
Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947). Эти опыты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881 —1948) и ранее шотландским физиком Б. Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах заряжены отрицательно, а их удельный заряд приблизительно одинаков для всех исследованных металлов.
По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали.
Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны.
Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.
Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается тер-
модинамическое равновесие между электронным газом и решеткой. По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории (см. (44.3)), можно найти среднюю скорость теплового движения электронов
которая для T=300 К равна 1,1•105 м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток.
Среднюю скорость упорядоченного движения электронов можно оценить согласно формуле (96.1) для плотности тока: j=ne.
Выбрав допустимую плотность тока, например для медных проводов 107 А/м2, получим, что при концентрации носителей тока n=8•1028 м-3 средняя скорость (v) упорядоченного движения электронов равна 7,8•10-4 м/с. Следовательно,
Классическая электронная теория проводимости Друде-Лоренца
Теория Друде была разработана в 1900 году, через три года после открытия электрона. Затем теория была доработана Лоренцом, и сейчас она является классической и актуальной теорией проводимости металлов.
Электронная теория Друде-Лоренца
Согласно теории, носителями тока в металлах являются свободные электроны.
Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют «электронный газ».
Двигаясь в металле, электроны соударяются между собой и с кристаллической решеткой (это и есть проявление электрического сопротивления проводника). Между соударениями электроны, по аналогии с длиной свободного пробега молекул идеального газа, успевают преодолеть средний путь λ.
Без действия электрического поля, ускоряющего электроны, кристаллическая решетка и электронный газ стремятся к состоянию теплового равновесия.
Приведем основные положения теории Друде:
- Взаимодействие электрона с другими электронами и ионами не учитывается между столкновениями.
- Столкновения являются мгновенными событиями, внезапно меняющими скорость электрона.
- Вероятность для электрона испытать столкновение за единицу времени равна 1τ.
- Состояние термодинамического равновесия достигается благодаря столкновениям.
Важно.
Несмотря на множество допущений, теория Друде-Лорецна хорошо объясняет эффект Холла, явление удельной проводимости и теплопроводность металлов. Именно поэтому она актуальна по сей день, хотя ответы на многие вопросы (например, почему в металле существуют свободные ионы и электроны) смогла дать только квантовая теория твердого тела.
В рамках теории Друде объясняется сопротивление металлов. Оно обусловлено соударениями электронов с узлами кристаллической решетки.
- Выделение тепла, согласно закону Джоуля-Ленца, также происходит по причине соударения электронов с ионами решетки.
- Теплопередача в металлах также осуществляется электронами, а не кристаллической решеткой.
- Терия Друде не объясняет многих явлений, как например сверхпроводимость, и не применима в сильных магнитных полях, в слабых магнитных полях может терять применимость из-за квантовых явлений.
- Среднюю скорость электронов можно вычислить по формуле для идеального газа:
- v=8kTπm
- Здесь k — постоянная Больцмана, T — температура металла, m — масса электрона.
- При включении внешнего электрического поля, на хаотичное движение частиц «электронного газа» накладывается упорядоченное движение электронов под действием сил поля, когда электроны начинают упорядоченно двигаться со средней скоростью u. Величину этой скорости можно оценить из соотношения:
- j=nqu,
- где j — плотность тока, n — концентрация свободных электронов, q — заряд электрона.
- При больших плотностях тока рассчеты дают следующий результат: средняя скорость хаотичного движения электронов во много раз (≈108) больше скорости упорядоченного движения под действием поля. При вычислении суммарной скорости полагают, что
- u→+v→≈v→
Формула Друде
- Формула Друде выводится из кинетического уравнения Больцмана и имеет вид:
- σ=nq2τm*
- Здесь m* — эффективная масса электрона, τ — время релаксации, то есть время, за которое электрон «забывает» о том, в какую сторону двигался после соударения.
- Друде вывел закон Ома для токов в металле:
- j=σ·E→
Опыт Толмена и Стюарта
В 1916 году опыт Толмена и Стюарта дал прямое доказательство тому, что носителями тока в металлах являются электроны.
Суть опыта была в следующем.
Опыт Толмена и Стюарта
Проводящая катушка с проводом длиной L вращалась вокруг своей оси с большой скоростью, а ее концы были замкнуты на гальванометр. Когда катушку резко тормозили, свободные электроны в металле продолжали двигаться по инерции, и гальванометр регистрировал импульс тока.
Считая, что свободные электроны подчиняются законам механики Ньютона, можно записать, что при остановке проводника электрон приобретает ускорение v' (в катушке направлено вдоль проводов). При этом на электрон действует сила, направленная противоположно ускорению.
- F=-mv'
- Под воздействием этой силы электрон ведет себя так, как если бы на него действовало поле E=-mv'q. Эдс, возникающую в катушке при торможении можно записать, как:
- ε=∫LEdl=-mv'q∫Ldl=-mv'qL
- Считая, что ускорение одинаково в каждом витке, можно записать закон Ома для катушки, а затем вычислить заряд, проходящий в ней за время dt:
- IR=-mv'qL
- dq=Idt=-mLdvqRdtdt=-mLdvqR
- Заряд, прошедший от момента начала торможения до остановки:
- q=-mLqR∫v00dv=-mLv0qR
- Опыт Толмена и Стюарта получил хорошее согласование с теорией, полученное экспериментально отношение qmсоответствовало отношению заряда электрона к его массе.
Пример
- При T=300К вычислите среднюю скорость теплового движения свободных электронов.
- Решение.
- Вычислим среднюю скорость, применяя формулу для идеального газа:
- v=8kTπm
- k=1,38·10-23 ДжК
- m=9,31·10-31кг
- Подставляем значения и вычисляем:
- v=8·1,38·10-23·3·1023,14·9,31·10-31≈105 мс






