- Сопротивление
- Коэффициент сопротивления
- Газы
- Жидкости
- Сверхпроводимость
- Применение
- Резистор
- Терморезистор
- Термометр сопротивления
- Газ
- Заключение
- Видео по теме
- Физика. 10 класс
- Электропроводность: объяснение, формулы, единица измерения, таблица
- Формулы
- Единица измерения
- Электропроводность металлов
- Таблица удельной электропроводности
- Влияние температуры металла на его электропроводность
- Большая Рнциклопедия Нефти Рё Газа
При проектировании электрических схем, инженеры сталкиваются с тем, что проводники обладают определенным сопротивлением, на которое оказывают влияния температурные колебания.
Статья даст подробное описание, что такое зависимость сопротивления от температуры и как температура влияет на проводимость различных веществ — металлов, газов и жидкостей.
Дополнительно будет приведена формула расчета такой зависимости.

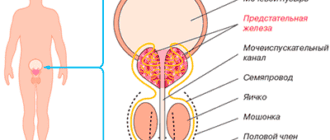
Сопротивление
Сопротивлением называется способность проводника пропускать через себя электрический ток. Единицей измерения данной физической величины является Ом. На принципиальных схемах эта величина обозначается буквой «R».
На величину сопротивления любого проводника электрическому току влияет его структура. Двигаясь внутри структуры, свободные электроны сталкиваются с атомами и электронами, которые замедляют их движение.
Чем их концентрация больше, тем выше будет само электрическое сопротивление.
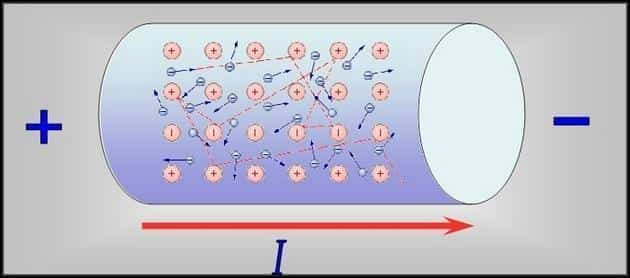
О способности проводников проводит электрический ток судят по величине его удельного сопротивления.
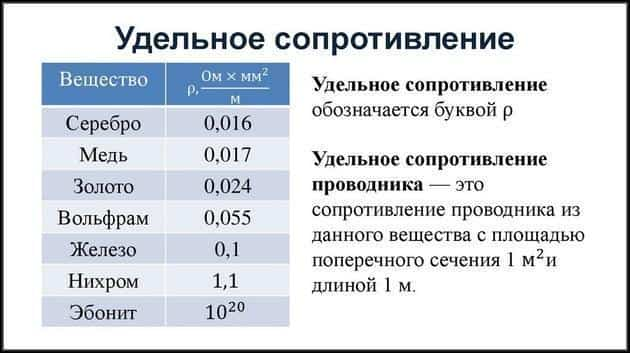
Удельное сопротивление проводника — это сопротивление протеканию тока через проводник из любого вещества с площадью поперечного сечения 1 м² и длиной один метр. Обозначается в физике данная величина буквой «ρ».
Данный параметр является табличной величиной и измеряется в системе СИ как Ом×м (может также измеряться в Ом×см и Ом×мм²/м).
Коэффициент сопротивления
Во время работы электрических цепей прослеживается прямая зависимость сопротивления металлов от температуры. Это явление называют коэффициентом температурного сопротивления. Оно определяет соотношение сопротивления к температурным изменениям.
Объясняется это явление следующим образом: с повышением температуры структура проводника получает долю тепловой энергии, вследствие чего эта энергия увеличивает скорость движения атомов. В результате повышается вероятность их столкновения со свободными электронами.
Чем чаще происходят эти столкновения, тем ниже будет проводимость.
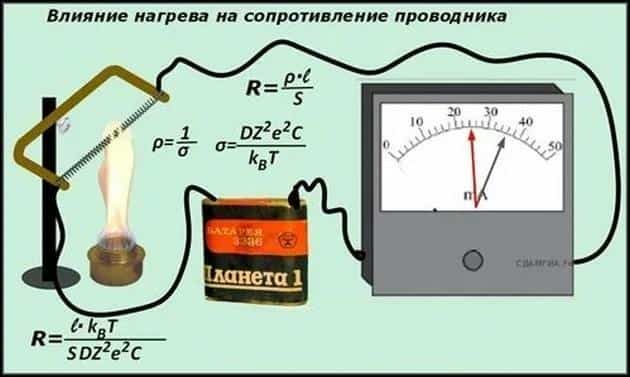
Можно провести простой опыт: в электрическую схему из аккумулятора и омметра подключим кусок медной проволоки. При таком подключении схема будет иметь строго определенное значение сопротивления.
Далее надо будет нагреть медную проволоку. В момент нагрева можно заметить, что сопротивление всей схемы растет, а после остывания проводника оно наоборот уменьшается.
На основании такого опыта довольно просто прослеживается температурная зависимость сопротивления проводника.
Температурный коэффициент отображает увеличение сопротивления при изменении температуры вещества на 1 градус. Для максимально чистого металла это значение равняется 0.004 °С-1.
То есть, при увеличении температуры на 10 градусов, электрическая проводимость в металлах изменится на 4 % в большую сторону. Данная величина обозначается буквой «α».
При расчете сопротивления через удельное сопротивление используется такая формула:
В данной зависимости:
- «R» — сопротивление, Ом;
- «l» — длина проводника, м;
- «s» — поперечное сечение проводника, м²;
- «ρ» — значение удельного сопротивления, Ом×м.
Зависимость проводимости металлического проводника от температуры можно проследить с помощью таких выражений:

Для металлов все предельно просто — изменение температуры приводит к увеличению его сопротивления. Ниже будет дано описание этой зависимости для газов, которые по своей природе являются диэлектриками.
Для закрепления материала, решим следующую задачу:
Имеется стальной проводник, диаметр которого равен один миллиметр, а длина его составляет 100 метров. Определите сопротивление такого проводника из стали, если величина удельного сопротивления стального проводника составляет 12×10-8 Ом×м.
- Решение:
- d=1 мм;
- l=100 м;
- ρ=13×10-8 Ом×м;
- R–?
- Определяем сопротивление проводника по формуле:
- R=ρ(l/S)
- где S является площадью поперечного сечения. Определить площадь можно с помощью формулы:
S= π×r2= π×d2/22=3.14×(1×10-3)2/4=3.14×10-6/4=0.785×10-6м2
После этого можно определить сопротивление:
R=12×10-8×100/(0.785×10-6)=15.287 Ом
Газы
Газы не являются проводниками, но их проводимость так же зависит от температуры. Происходит это за счет так называемого эффекта ионизации. Ионизация в газах происходит за счет насыщения их жидкостью или иными веществами, которые способны проводить электрический ток. Проследить то, как увеличивается сопротивление при повышении температуры газа можно на таком опыте.

К схеме с амперметром и аккумулятором добавим 2 металлические пластины, которые не соприкасаются друг с другом. Такая электрическая цепь является разомкнутой. Между пластинами поместим зажженную горелку. При нагреве происходит смещение стрелки амперметра в сторону увеличения. То есть такую цепь можно считать замкнутой.
На основании этого можно сделать вывод, что с ростом температуры воздух ионизируется, происходит снижение его сопротивления и увеличение проводимости заряженных электронов. Данный эффект называют пробоем изоляционного слоя газа, зависящий от степени их ионизации и величины протекающего напряжения.
Подобное явление знакомо каждому из нас — это грозовой разряд.
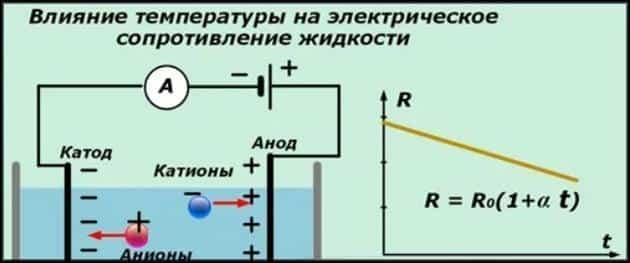
Жидкости
В жидкостях прослеживается обратная зависимость. С увеличением температуры, сопротивление жидкого проводника уменьшается. Для электролита свойственно правило отрицательного значения температурного коэффициента — а˂0. Удельное сопротивление электролита рассчитывается следующим образом:
ρ= ρ0(1+ αt) или R=R0(1+ αt), где а˂0.
При этом увеличившееся значение температуры электролита сопровождается уменьшением сопротивления и ростом его проводимости.
Сверхпроводимость
Снижение температуры металлических проводников сильно увеличивает их проводимость.
Это связано с тем, что в структуре вещества замедляется движение атомов и электронов, благодаря чему снижается вероятность их столкновения со свободными электронами.
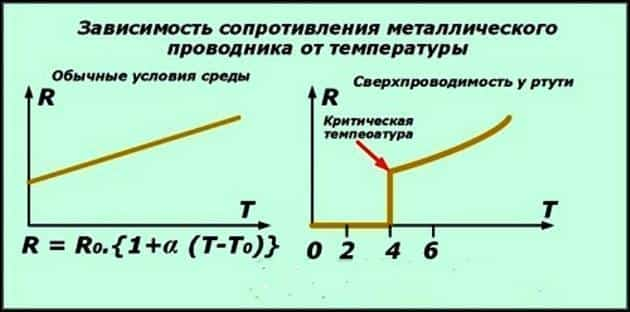
При температуре абсолютного 0 (–273 градуса Цельсия) возникает явление падения до нуля сопротивления проводника. Зависимость сопротивления проводника от температуры при абсолютном 0 — сверхпроводимость.
Температура, при которой обычный проводник становится сверхпроводником, называется критической. Она будет разной для различных чистых металлов и сплавов. Все будет зависеть от их структуры, химического состава и структуры кристаллов.
Например, серое олово с алмазной структурой является полупроводником. Но белое олово при своей тетрагональной кристаллической ячейке, мягкости и плавкости, переходит в состояние сверхпроводника при температуре 3.70 К.
Также при критической температуре прослеживается целый ряд других способностей:
- Повышение частоты переменного тока вызывает рост сопротивления, значение гармоник с периодом световой волны.
- Способность удерживать величину силы тока ранее приложенного, а затем отключенного источника.
Металл или сплав может перейти в состояние сверхпроводника и при нагревании. Такое явление называют высокотемпературной проводимостью. Ответ на вопрос, почему от высокой температуры сопротивление металлов снижается, может довольно просто объяснить их кристаллическая структура.
В момент нагрева до критических значений, электроны перестают хаотично перемещаться внутри структуры вещества. Они выстраиваются в цепочку. Такое построение не мешает движению свободных электронов, а значит падает общее сопротивление.
Переход в состояние высокотемпературной проводимости начинается с порога 1000К и этот показатель выше, чем точка кипения азота.
Применение
Свойство проводников изменять сопротивление при определённой температуре используют для создания различных элементов электрических схем и измерительных приборов. О них будет рассказано далее в данной статье.
Резистор
Сопротивление устройств старого типа сильно зависело от их нагрева. При нагревании проводимость резистора пропорционально изменялась в меньшую сторону.
Для электрических цепей требуется идеальный резистор, который обладает наивысшим коэффициентом проводимости.
Для снижения нагрева при производстве данных устройств теперь используется материал, имеющий малую зависимость сопротивления от температуры нагрева. Это позволило применять резисторы с малым сопротивлением для цепей с большим напряжением.
Терморезистор
Существует отдельная группа резисторов, которые применяют для измерения температуры. Особенностью такого устройства является то, что он может снижать свою проводимость при нагреве. При этом он отключает цепь при достижении определенного порогового значения.
Термометр сопротивления
Это прибор был разработан для измерения температуры среды. Он состоит из тонкой платиновой проволоки, защитного чехла и корпуса. Прибор имеет стабильную реакцию на перепады температуры. Измеряемой величиной в данном устройстве служит сопротивление этой проволоки из платины. Чем выше будет температура, тем сопротивление соответственно будет больше.
Понижение сопротивления так же фиксируется, так как в этот момент меняются проводимость и сопротивление. Для измерения температуры термометром сопротивления, в настоящее время применяются проволочные индикаторы из разнообразных металлов. В зависимости от свойств используемого металла, погрешность устройства может составлять не более 0.1 %.
Благодаря этому достигается очень высокая точность измерения температуры.
Газ
Самый известный нам газовый проводник — это люминесцентная лампа. Газ нагревается за счет увеличения напряжения между анодом и катодом лампы.
Известным жидкостным проводником является щелочной аккумулятор. При понижении температуры нарушается структура жидкости и изменяется ее сопротивление.
Нагрев провоцирует движение атомов и электронов, увеличивая сопротивление и зарядный ток устройства.
Заключение
В данной статье мы рассмотрели, как зависит сопротивление от температуры. Металлы, газы и жидкости имеют свойства изменять свою проводимость и сопротивление при температурных перепадах.
Это свойство изменения электрического сопротивления используются для измерения температуры среды.
Наибольшая точность измерений температуры в настоящее время достигается за счет применения современных материалов, даже в бытовой технике.
Видео по теме
Физика. 10 класс
Типичными представителями класса проводников являются металлы. Какова природа электрического тока в металлах?
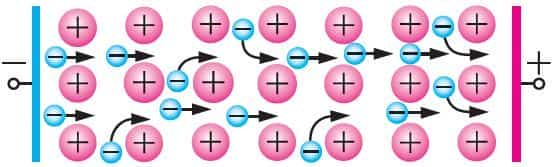 Рис. 194
Рис. 194
Природа электрического тока в металлах. В металлических проводниках носители электрического заряда — свободные электроны. Под действием внешнего электрического поля свободные электроны упорядоченно движутся, создавая электрический ток (рис. 194).
Рис. 195
Электронная проводимость металлов была впервые экспериментально подтверждена немецким физиком К. Рикке (1845–1915) в 1901 г. Суть опыта Рикке заключалась в следующем: по проводнику, состоявшему из трёх отполированных и плотно прижатых друг к другу цилиндров — двух медных и одного алюминиевого (рис. 195), в течение года проходил ток одного и того же направления.
За этот промежуток времени через проводник прошёл заряд более 3,5 МКл. После завершения опыта взвешивание показало, что массы цилиндров остались неизменными.
Это явилось экспериментальным доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются одинаковыми для всех металлов, т. е. электронами.
В 1916 г. американский физик Р. Толмен (1881—1948) и шотландский физик Т. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением свободных электронов.
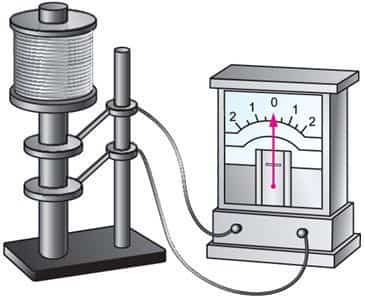 Рис. 195.1
Рис. 195.1
В этих опытах катушку с большим числом витков тонкой проволоки подключали к гальванометру и приводили в быстрое вращение вокруг своей оси (рис. 195.1). При резком торможении катушки в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда.
По направлению отклонения стрелки гальванометра было установлено, что электрический ток создают отрицательно заряженные частицы. При этом экспериментально полученное отношение заряда каждой из этих частиц к её массе (удельный заряд) близко к удельному заряду электрона, полученному из других опытов.
Так было экспериментально доказано, что носителями свободных зарядов в металлах являются электроны.
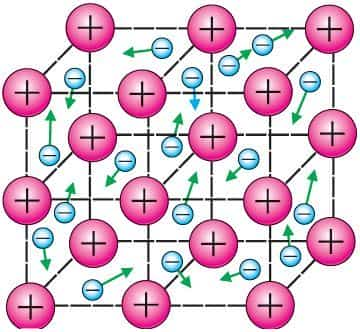 Рис. 196
Рис. 196
Вещества, обладающие электронной проводимостью, называют проводниками первого рода.
В соответствии с классической электронной теорией проводимости металлов, созданной немецким физиком П. Друде (1863–1906) в 1900 г., металлический проводник можно рассматривать как физическую систему, состоящую из свободных электронов и положительно заряженных ионов, колеблющихся около положений равновесия (рис. 196).
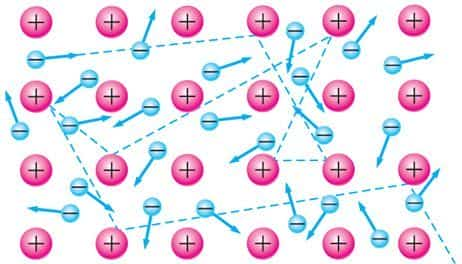 Рис. 196.1
Рис. 196.1
Появление свободных электронов при образовании металлического кристалла из нейтральных атомов можно упрощённо объяснить следующим образом. Электроны, находящиеся на внешних оболочках атомов, слабо связаны со своими ядрами.
При образовании кристалла атомы сближаются на расстояние r 0,1 нм, и электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов.
В результате этого их взаимодействие с собственными ядрами значительно ослабевает, вследствие чего они теряют с ними связь и могут двигаться по всему кристаллу в любом направлении как свободные частицы. Атомы превращаются при этом в положительно заряженные ионы.
В пространстве между ионами беспорядочно движутся подобно частицам идеального газа свободные электроны. Поэтому для описания движения электронов используют модель «электронный газ» — совокупность свободных электронов в кристаллической решётке металла. На рисунке 196.1 пунктирной линией изображена траектория движения одного из электронов.
В этой модели электроны, упорядоченное движение которых является током проводимости, рассматривают как материальные точки, модуль потенциальной энергии взаимодействия которых пренебрежимо мал по сравнению с их кинетической энергией.
Считают, что движение электронов под действием электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими, т. е. при столкновениях электроны полностью передают ионам кинетическую энергию своего упорядоченного движения.
В промежутках между столкновениями свободные электроны совершают беспорядочное тепловое движение и в то же время движутся упорядоченно и равноускоренно под воздействием электрического поля.
Интересно знать
Модель электронного газа позволяет теоретически объяснить природу сопротивления и обосновать закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов. Проанализируем упорядоченное движение электронов проводимости.
Пусть электрон движется с ускорением в направлении, противоположном направлению напряжённости электрического поля (рис. 196.2): где m0 — масса электрона, e — элементарный электрический заряд (модуль заряда электрона).
 Рис. 196.2
Рис. 196.2
Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля где l — длина проводника, U — напряжение между его концами. Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника .
Сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:
где q — модуль заряда электронов проводимости, находящихся в проводнике, — усреднённое время прохождения этих электронов по проводнику, N — количество электронов проводимости в проводнике, n — концентрация этих электронов, V = Sl — объём проводника. Следовательно, сила тока пропорциональна напряжению между концами проводника I U.
Электропроводность: объяснение, формулы, единица измерения, таблица
Почему медь проводит электричество лучше, чем вода? Прочитав эту статью, вы больше не будете задавать себе больше этот вопрос. Далее мы обсудим электропроводность и рассмотрим формулы, которые описывают это понятие. Наконец, вы можете проверить свои знания на двух примерах.
Простое объяснение.
Электропроводность – это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.
Формулы
Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). В дальнейшем мы будем использовать σ. Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:
σ = 1 / ρ .
Здесь ρ называется удельным сопротивлением. Вы можете рассчитать электрическое сопротивление R проводника с учетом его параметров следующим образом: R = ( ρ * l ) / S .
Таким образом, сопротивление R равно удельному сопротивлению ρ , умноженному на длину проводника l, деленному на площадь поперечного сечения S. Если теперь вы хотите выразить эту формулу через удельную электропроводность σ = 1 / ρ , полезно знать, что электрическая проводимость G проводника выражается следующим образом: G = 1 / R .
- Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1 / G = ( 1 / σ ) * ( l / S ) .
- Путем дальнейшего преобразования можно получить выражение: G = σ * S / l .
- С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J = σ * E .
Единица измерения
Единицей удельной электропроводности σ в СИ является: [ σ ] = 1 См/м ( Сименс на метр ).
Эти единицы определяются по формуле G = σ * S / l . Если решить эту формулу в соответствии с σ, то получим σ = G * l / S .
- Единица измерения электрической проводимости G задается как: [ G ] = 1 / σ = 1 См ( Сименс, международное обозначение: S ).
- Если теперь ввести в формулу все единицы измерения, то получится:
- [ σ ] = 1 См * 1 м / м2 = 1 См / м .
Вы также будете чаще использовать единицы измерения См / см , м / Ом * мм2 или См * м / мм2 . Вы можете преобразовать отдельные измеряемые переменные так: См / см = См / 10-2 м и так: м / Ом * мм2 = См * м / мм2 = См * м / 10-3 м * 10-3 м = 106 См / м .
Электропроводность металлов
В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.
В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ.
Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.
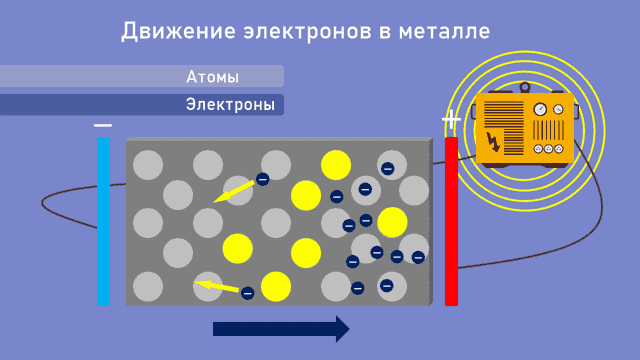 Рис. 1. Движение электронов в металле
Рис. 1. Движение электронов в металле
На рисунке 1 видно, что некоторые электроны не могут быть притянуты непосредственно к положительному полюсу, потому что на пути стоит, так сказать, твердое атомное ядро. Там они замедляются и в некоторой степени отклоняются. Именно поэтому электроны не могут ускоряться в металле бесконечно, и именно так возникает удельное сопротивление или электропроводность.
Теперь вы также можете измерить удельную электропроводность в металле с помощью следующей формулы: σ = ( n * e2 * τ ) / m .
В этой формуле n означает число электронов, e – заряд электрона, m – массу электрона, а τ – среднее время полета электрона между двумя столкновениями.
Таблица удельной электропроводности
Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице ниже. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.
| Вещество | Удельная электропроводность в См / м |
| Серебро | 62 · 106 |
| Медь | 58 · 106 |
| Золото | 45,2 · 106 |
| Алюминий | 37,7 · 106 |
| Вольфрам | 19 · 106 |
| Латунь | 15,5 · 106 |
| Железо | 9,93 · 106 |
| Нержавеющая сталь (WNr. 1,4301) | 1,36 · 106 |
| Германий (легирование |
Влияние температуры металла на его электропроводность
При снижении температуры утихают колебания кристаллической решётки, это облегчает прохождение электронов и электропроводность металлических проводников возрастает, а сопротивление уменьшается.
Рассмотрим график типичной зависимости удельного электрического сопротивления проводника от температуры на примере меди (рисунок 2.2).
В широком диапазоне температур увеличение сопротивления пропорционально увеличению температуры, на графике это выглядит как прямолинейный наклонный участок.
Рост сопротивления представляет собой повышение рассеяния электронов из-за усиления тепловых колебаний ионов и связанной с ними флуктуации электростатического поля кристаллической решётки.
Относительное изменение удельного электрического сопротивления при изменении температуры на один градус Кельвина называют температурным коэффициентомудельного электрического сопротивления; обозначают какТКρ или αρ, у меди αρ = 4,33 · 10–3 К–1.
Для большинства металлов ТКρ составляет несколько тысячных долей на кельвин; от 0,9 · 10–3 К–1 у ртути, до 6,7 · 10–3 К–1 у никеля.
- В пределах прямолинейного участка температурной характеристики справедливо соотношение
- ρ2 = ρ1[1 + αρ(Т2– Т1)],
- где ρ1 и ρ2 – значения удельных электрических сопротивлений, соответству-
- ющих значениям температуры Т1 и Т2;
- αρ – температурный коэффициент удельного электрического
- сопротивления.
| Рисунок 2.2 – Зависимость удельного электрического сопротивления меди ρ от температуры |
В особо чистых металлах при сверхнизких температурах наблюдается криопроводимость, при этом сопротивление стремится к значению ρ0, называемому остаточным сопротивлением (этот участок показан на рисунке 2.
2 в увеличенном виде). Остаточное сопротивление обусловленное примесями и дефектами структуры, в тысячи раз ниже, чем сопротивление при комнатной температуре. Правило Матиссена позволяет представить удельное электрическое сопротивление проводника ρ как сумму тепловой составляющей ρт и остаточного сопротивления ρ0,
- ρ = ρт + ρ0,
- где ρт – тепловая составляющая удельного электрического сопротивления;
- ρ0 – остаточное удельное электрическое сопротивление.
Тепловая составляющая сопротивления ρт растёт пропорционально значению температуры, на рисунке 2.2 она показана прямой наклонной линией. Остаточное сопротивление практически не зависит от температуры (на рисунке ρ0 – горизонтальная линия).
У некоторых металлов в области сверхнизких температур, ниже 10 К, возможна скачкообразная потеря сопротивления – сверхпроводимость.
Металлическую медь в сверхпроводящее состояние перевести не смогли, однако оксид меди является основой купратных сверхпроводников.
В правой части графика, при температурах, близких к плавлению, также возможно нарушение линейности, особенно у ферромагнитных материалов. Это связано с перегруппировками электронов в оболочках и изменением формы кристаллов, т. е. представляет собой проявление полиморфизма.
При плавлении меди, в результате уменьшения плотности и нарушения кристаллического порядка, её удельное сопротивление возрастает в 2,4 раза. Для большинства металлов такое увеличение происходит в пределах от 1,5 до 3 раз; исключение составляют галлий и висмут, плотность которых при плавлении возрастает, а удельное электрическое сопротивление уменьшается.
Влияние примесей и других структурных дефектов на электропроводность металлов
Примеси снижают электропроводность в любом случае, даже если электропроводность металла примеси выше, чем у основного металла; это вызвано нарушением правильности структуры.
Степень снижения электропроводности зависит от количества и состава примеси. Если ввести в медь серебро в количестве 0,5 %, то её электропроводность уменьшится на 1 %.
Добавка в медь такого же количества кадмия снизит её электропроводность на 2 %, а цинка – на 5 %.
Примеси других элементов влияют на электропроводность меди гораздо заметнее.
Для снижения электропроводности меди вдвое достаточно присутствие любой из перечисленных добавок: 1,2 % никеля; 1,1 % олова; 0,8 % алюминия; 0,4 % бериллия; 0,2 % железа или кремния; 0,1 % фосфора.
Экспериментально установлено, что при малом содержании примесей удельное сопротивление металла возрастает пропорционально увеличению количества атомов каждой из примесей, таким образом, эффекты от влияния нескольких различных примесей складываются.
- Собственные дефекты структуры металла – вакансии, атомы внедрения, дислокации, границы зёрен – также увеличивают его удельное электрическое сопротивление.
- Для оценки химической чистоты и структурного совершенства металлов используют значение остаточного сопротивления ρ4,2, измеренное при температуре жидкого гелия (4,2 К), а также параметр β, равный отношению значений сопротивления при комнатной температуре (300 К) и при температуре жидкого гелия:
- β = ρ300 / ρ4,2.
- Для наиболее чистых металлов, получаемых в настоящее время (со степенью чистоты 99,99999 %), параметр β достигает порядка 105.
Заметное влияние на удельное сопротивление металлов и сплавов оказывают искажения, вызываемые напряжённым состоянием материала. Например, при всестороннем сжатии у большинства металлов удельное сопротивление уменьшается. Это объясняется сближением атомов и уменьшением амплитуды тепловых колебаний решётки.
При упругомрастяжении и кручении межатомные расстояния увеличиваются, что вызывает возрастание ρ.
Пластическая деформация и наклепвсегда повышают удельное сопротивление металлов и сплавов, однако это повышение, даже при значительном наклепе чистых металлов, составляет единицы процентов.
Термическая закалка приводит к повышению ρ, что связано с перестройкой кристаллической решётки и появлением внутренних напряжений. При рекристаллизации металлического изделия путём термической обработки (отжига) удельное электрическое сопротивление материала может быть снижено до первоначального значения за счёт снятия внутренних напряжений.
Большая Рнциклопедия Нефти Рё Газа
Cтраница 1
Рлектрическая проводимость металлов обусловлена наличием РІ РёС… кристаллических решетках свободных электронов, движение которых РїСЂРё наложении электрического поля даже небольшого напряжения получает направленность. РЎ повышением температуры электрическая проводимость металлов уменьшается, так как РїСЂРё этом колебательные движения РёРѕРЅРѕРІ РІ узлах кристаллической решетки металлов усиливаются, что препятствует направленному движению электронов. Наоборот, СЃ понижением температуры электрическая проводимость увеличивается, Рё РІ области, близкой Рє абсолютному нулю, Сѓ РјРЅРѕРіРёС… металлов наблюдается сверхпроводимость. Значения электрической проводимости Сѓ различных металлов сильно расходятся. Р�С… сравнение, однако, затруднено, так как РїСЂРё одинаковой температуре амплитуда колебаний атомов, РѕС‚ которой зависит электрическая проводимость, Сѓ разных металлов различна. [1]
Рлектрическая проводимость металла определяется произведением концентрации электронов РЅР° РёС… подвижность.
Подвижность электронов ип есть скорость, измеренная в см / сек, в поле, градиент которого равен 1 в [ см.
Наряду с шириной запрещенной зоны АЕ, продолжительностью жизни т и концентрацией носителей зарядов при собственной проводимости, подвижность электронов ип представляет собой четвертую существенную величину, характеризующую полупроводник. В случае беспримесных полупроводников к току, образуемому электронами, добавляется еще ток, образуемый дырками. [2]
Рлектрическая проводимость металла зависит РѕС‚ числа Рё заряда электронов, участвующих РІ переносе тока, Рё среднего времени пробега между столкновениями. Рти же параметры РїСЂРё данной напряженности электрического поля определяют Рё скорость движения электрона. [3]
Рлектрическая проводимость металлов сильно зависит РѕС‚ температуры.
С повышением температуры колебательные движения ионов в узлах решетки усиливаются, а это, в свою очередь, очень препятствует направленному движению электронов. [5]
Рлектрическая проводимость металлов сильно зависит РѕС‚ температуры.
С понижением температуры тепловые колебания ионов в узлах сильно уменьшаются и электрическая проводимость увеличивается.
При температурах, близких к абсолютному нулю, у большинства металлов проявляется сверхпроводимость. [6]
На электрическую проводимость металлов и сплавов влияют температура, концентрация примесей и атомы с некомпенсированными электронами. [7]
При изменении электрической проводимости немагнитных металлов от нуля, до бесконечности вносимое индуктивное сопротивление изменяется от нуля до некоторого предельного значения.
РџСЂРё контроле ферромагнитных материалов знак РІРЅРѕСЃРёРјРѕРіРѕ сопротивления зависит РѕС‚ частоты. РќР° РЅРёР·РєРёС… частотах РІРЅРѕСЃРёРјРѕРµ индуктивное сопротивление положительно, Р° РЅР° высоких — отрицательно.
[8]
Становится понятной и электрическая проводимость металлов. [10]
В отличие от полупроводников электрическая проводимость металлов мало зависит от имеющихся в их структуре примесных дефектов.
Однако примесные дефекты могут оказывать существенное влияние на другие свойства металлов.
Так, механические характеристики металлов сильно зависят от наличия в их структуре междоузельных примесных дефектов.
С учетом плотнейшей упаковки металлических кристаллов в междоузлия способны попадать лишь микрочастицы небольших размеров, такие, как атомы водорода, углерода, кислорода, азота.
Кристаллы многих металлов часто поглощают большое количество указанных примесей. Например, количество водорода, поглощенного палладием или цирконием, обычно настолько велико, что его атомы заполняют почти все междоузлия в кристаллах указанных металлов. [12]
От чего зависит теплопроводность и электрическая проводимость металлов. [13]
В отличие от полупроводников, электрическая проводимость металлов понижается с повышением температуры. Однако и в жидком ( расплавленном) состоянии металлы проводят электрический ток. [14]
Р’ настоящее время различия РІ электрической проводимости металлов, полупроводников Рё изоляторов РѕР±СЉСЏСЃРЅСЏСЋС‚ РЅР° РѕСЃРЅРѕРІРµ квантовой теории строения кристаллических веществ или так называемой теории энергетических Р·РѕРЅ. Сущность ее состоит РІ следующем. Рлектроны ближайших Рє СЏРґСЂСѓ энергетических уровней атомов полностью насыщают эти СѓСЂРѕРІРЅРё, находятся РІ устойчивых состояниях Рё образуют так называемую заполненную валентную Р·РѕРЅСѓ. Рлектрическая проводимость Рё теплопроводность вещества РЅРµ связаны СЃ электронами этой Р·РѕРЅС‹. Р’ электрической проводимости РјРѕРіСѓС‚ участвовать только электроны ненасыщенных энергетических уровней. РџСЂРё этом полосы основных Рё возбужденных ( периферических) энергетических уровней разделяются промежуточными свободными полосами, которые РЅРµ имеют возможных для электрона квантовых состояний. Рту энергетическую Р·РѕРЅСѓ, промежуточную между зонами основных Рё возбужденных уровней, называют запрещенной Р·РѕРЅРѕР№. [15]
Страницы: 1 2 3 4