- Квантовая теория проводимости металлов
- Понятие о квантовой теории электропроводности металлов
- Физики смоделировали поведение странных металлов
- Квантовая теория электропроводности металла
- Сверхпроводимость металлов в квантовой физике
- Распределение Ферми-Дирака
- Движение электронов в кристаллической решетке
- Простейшая квантовая теория электропроводности металлов
- 3.6. Понятие о квантовой теории электропроводности металлов
Электропроводность есть способность тела пропускать электрический ток под действием электрического поля. Для характеристики этого явления служит величина удельной электропроводности σ.
Как показывает теория [1-3], величину σ можно выразить через концентрацию n свободных носителей заряда, их заряд е, массу m, время свободного пробега τe, длину свободного пробега λe и среднюю дрейфовую скорость < v > носителей заряда.
Для металлов в роли свободных носителей заряда выступают свободные электроны, так что:
- σ = ne2 · τе / m = (n · e2 / m) · (λe / < v >) = e · n · u
- (10.1)
- u = < v > / E = (e · τе) / m
- В зависимости от σ все вещества подразделяются; на проводники — с σ > 106 (Ом · м)-1, диэлектрики — с σ > 10-8 (Ом · м)-1 и полупроводники — с промежуточным значением σ.
где u — подвижность носителей, т.е.
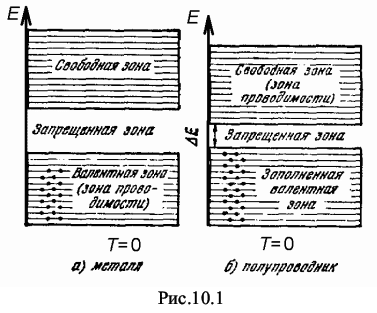
физическая величина, численно равная дрейфовой скорости, приобретенной носителями в поле единичной напряженности , а именноС точки зрения зонной теории деление веществ на проводники, полупроводники и диэлектрики определяется тем, как заполнена электронами при 0 К валентная зона кристалла: частично или полностью.
Энергия, которая сообщается электронам даже слабым электрическим полем, сравнима с расстоянием между уровнями в энергетической зоне. Если в зоне есть свободные уровни, то электроны, возбужденные внешним электрическим полем, будут заполнять их. Квантовое состояние системы электронов будет изменяться, и в кристалле появится преимущественное (направленное) движение электронов против поля, т.е. электрический ток. Такие тела (рис.10.1,а) являются проводниками.
Если валентная зона заполнена целиком, то изменение состояния системы электронов может произойти только при переходе их через запрещенную зону. Энергия внешнего электрического поля такой переход осуществить не может.
Перестановка электронов внутри полностью заполненной зоны не вызывает изменения квантового состояния системы, т.к. сами по себе электроны неразличимы.
В таких кристаллах (рис. 10.1,б) внешнее электрическое поле не вызовет появление электрического тока, и они будут непроводниками (диэлектриками).
Из этой группы веществ выделены те у которых ширина запрещенной зоны ΔE ≤ 1 эВ (1эВ = 1,6 · 10-19 Дж).
Переход электронов через запрещенную зону у таких тел можно осуществить, например, посредством теплового возбуждения. При этом освобождается часть уровней — валентной зоны и частично заполняются уровни следующей за ней свободной зоны (зоны проводимости). Эти вещества являются полупроводниками.
Согласно выражению (10.1) изменение электропроводности (электрического сопротивления) тел с температурой может быть вызвано изменением концентрации n носителей заряда или изменением их подвижности u .
Квантово-механические расчеты показывают, что для металлов концентрация n свободных носителей заряда (электронов) равна:
- n = (1 / 3π2) · (2mEF / ђ2)3/2
- (10.2)
- где ђ = h / 2π = 1,05 · 10-34 Дж · с — нормированная постоянная Планка, EF — энергия Ферми.
Так как EF практически от температуры T не зависит, то и концентрация носителей заряда от температуры не зависит. Следовательно, температурная зависимость электропроводности металлов будет полностью определяться подвижностью u электронов, как и следует из формулы (10.1).
Тогда в области высоких температур
- u ~ λe / ~ T-1
- (10.3)
- u ~ λe / ~ const (T).
- (10.4)
а в области низких температур
Степень подвижности носителей заряда будет определяться процессами рассеяния, т.е. взаимодействием электронов с периодическим полем решетки.
Так как поле идеальной решетки строго периодическое, а состояние электронов — стационарное, то рассеяние (возникновение электрического сопротивления металла) может быть вызвано только дефектами (примесными атомами, искажениями структуры и т.д.) и тепловыми колебаниями решетки (фононами).
Вблизи 0 К , где интенсивность тепловых колебаний решетки и концентрация фононов близка к нулю, преобладает рассеяние на примесях (электрон-примесное рассеяние). Проводимость при этом практически не меняется, как следует из формулы (10.4), а удельное сопротивление
имеет постоянное значение, которое называется удельным остаточным сопротивлением ρост или удельным примесным сопротивлением ρприм, т.е.
ρост (или ρприм) = const (T)
(10.5)
В области высоких температур у металлов становится преобладающим электрон-фононный механизм рассеяния. При таком механизме рассеяния электропроводность обратно пропорциональна температуре, как видно из формулы (10.
3), а удельное сопротивление прямо пропорционально температуре:График зависимости удельного сопротивления ρ от температуры приведен на рис. 10.2При температурах отличных от 0 К и достаточно большом количестве примесей могут иметь место как электрон-фононное, так и электрон-примесное рассеяние; суммарное удельное сопротивление имеет видρ = ρприм + ρф
(10.6)
Выражение (10.6) представляет собой правило Матиссена об аддитивности сопротивления. Следует отметить, что как электрон-фононное, так и электрон-примесное рассеяние носит хаотический характер.
Квантово-механические расчеты подвижности носителей в полупроводниках показали, что, во-первых, с повышением температуры подвижность носителей u убывает, и решающим в определении подвижности является тот механизм рассеяния, который обуславливает наиболее низкую подвижность.
Во-вторых, зависимость подвижности носителей заряда от уровня легирования (концентрации примесей) показывает, что при малом уровне легирования подвижность будет определяться рассеянием на колебаниях решетки и, следовательно, не должна зависеть от концентрации примесей.
При высоких уровнях легирования она должна определяться рассеиванием на ионизированной легирующей примеси и уменьшаться с увеличением концентрации примеси. Таким образом, изменение подвижности носителей заряда не должно вносить заметного вклада в изменение электрического сопротивления полупроводника.
В соответствии с выражением (10.1) основной вклад в изменение электропроводности полупроводников должно вносить изменение концентрации п носителей заряда [1-3].
Главным признаком полупроводников является активационная природа проводимости, т.е. резко выраженная зависимость концентрации носителей от внешних воздействий, как-то температуры, облучения и т.д. Это объясняется узостью запрещенной зоны (ΔЕ < 1 эВ) у собственных полупроводников и наличием дополнительных уровней в запрещенной зоне у примесных полупроводников.
- Электропроводность химически чистых полупроводников называется собственной проводимостью. Собственная проводимость полупроводников возникает в результате перехода электронов (n) с верхних уровней валентной зоны в зону проводимости и образованием дырок (p) в валентной зоне:
- σ = σn + σρ = e · nn · un + e · nρ · uρ
- (10.7)
где nn и· nρ — концентрация электронов и дырок,un и uρ — соответственно их подвижности,e — заряд носителя.С повышением температуры концентрация электронов в зоне проводимости и дырок в валентной зоне экспоненциально возрастает:
- nn = unо · exp(-ΔE / 2kT) = nρ = nρо· exp(-ΔE / 2kT)
- (10.8)
- где nnо и npо — концентрации электронов и дырок при Т → ∞,
k = 1,38 · 10–23 Дж/ К — постоянная Больцмана.На рисунке 10.3,а приведен график зависимости логарифма электропровод-ности ln σ собственного полупроводника от обратной температуры 1 / Т : ln σ = = ƒ(1 / Т). График представляет собой прямую, по наклону которой можно опреде-лить ширину запрещенной зоны ∆Е.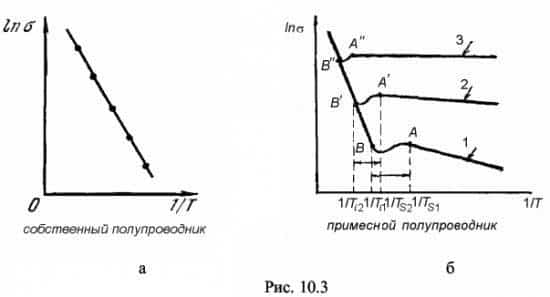 Электропроводность легированных полупроводников обусловлена наличием в них примесных центров. Температурная зависимость таких полупроводников определяется не только концентрацией основных носителей, но и концентрацией носителей, поставляемых примесными центрами. На рис. 10.3,б приведены графики зависимости ln σ = ƒ (1 / Т) для полупроводников с различной степенью легирования (n1 < n2 < n3, где n – концентрация примеси).
Электропроводность легированных полупроводников обусловлена наличием в них примесных центров. Температурная зависимость таких полупроводников определяется не только концентрацией основных носителей, но и концентрацией носителей, поставляемых примесными центрами. На рис. 10.3,б приведены графики зависимости ln σ = ƒ (1 / Т) для полупроводников с различной степенью легирования (n1 < n2 < n3, где n – концентрация примеси).
Для слаболегированных полупроводников в области низких температур преобладают переходы с участием примесных уровней. С повышением температуры растет концентрация примесных носителей, значит растет и примесная проводимость. При достижении т. А (см. рис. 10.3,б; кривая 1) – температуры истощения примеси ТS1 – все примесные носители будут переведены в зону проводимости.
Выше температуры ТS1 и до температуры перехода к собственной проводимости Тi1 (см. т. В, кривая 1, рис. 10.3,б) электропроводность падает, а сопротивление полупроводника растет.
Выше температуры Тi1 преобладает собственная электропроводность, т.е. в зону проводимости вследствие теплового возбуждения переходят собственные носители заряда.
В области собственной проводимости σ растет, а ρ падает.
Для сильнолегированных полупроводников, у которых концентрация примеси n ~ 1026 м–3, т.е. соизмерима с концентрацией носителей заряда в металлах (см. кривая 3, рис. 10.3,б), зависимость σ от температуры наблюдается только в области собственной проводимости. С ростом концентрации примесей величина интервала АВ (АВ > A'B' > A»B») уменьшается (см. рис. 10.3,б).
Как в области примесной проводимости, так и в области собственной проводимости преобладает электрон-фононный механизм рассеяния. В области истощения примеси (интервалы AB, A'B', A»B») вблизи температуры ТS преобладает электрон-примесное рассеяние.
По мере увеличения температуры (перехода к Тi) начинает преобладать электрон-фононное рассеяние.
Таким образом, интервал АВ (A'B' или A»B»), называемый областью истощения примеси, является также областью перехода от механизма примесной проводимости к механизму собственной проводимости.
Квантовая теория проводимости металлов
Электроны проводимости в металле образуют идеальный газ. Электроны являются фермионами с полуцелым спином, для них выполняется принцип Паули: в одном состоянии не может быть два электрона с четырьмя одинаковыми квантовыми числами. Эти электроны должны отличаться хотя бы магнитным спиновым квантовым числом, т.е. спины электронов направлены противоположно.
При температуре 0 К электроны занимают нижние квантовые состояния, по два электрона с одинаковой энергией, но противоположно направленными спинами.
Рис. 22.3.1 Рис. 22.3.2
Высший уровень, занятый электронами при Т = 0, называется уровнем Ферми, а соответствующая ему энергия – энергией Ферми. Энергией Ферми называется максимальная кинетическая энергия электронов в металле при температуре 0 К (рис. 21.3.1).
С ростом температуры выше 0 К энергия электронов увеличивается и они начинают переходить в состояния с большей энергией (рис. 21.3.2).
По квантовой теории электропроводимость металлов имеет почти такой же вид, как в классической физике
— средняя длина свободного пробега электронов, имеющих энергию Ферми; — средняя скорость теплового движения таких электронов.
По квантовой теории движению электронов можно сопоставить волновой процесс. В идеальной кристаллической решетке нет дефектов, т.е. существует идеальная периодичность в расположении атомов в узлах и атомы неподвижны. В этом случае электронные волны не рассеиваются, огибая узлы, поэтому нет сопротивления электрическому току.
В реальной кристаллической решетке всегда есть дефекты и тепловые колебания атомов в узлах. Происходит рассеяние электронных волн на неоднородностях и атомах, возникает сопротивление.
Удельное сопротивление равно , удельная проводимость обратно пропорциональна скорости электронов (22.3.1), поэтому сопротивление металла пропорционально , что не подтверждается экспериментально.
Сопротивление металла, как следует из эксперимента, зависит от температуры по шкале Цельсия линейно
или сопротивление металла пропорционально абсолютной температуре в первой степени
.
По квантовой теории средняя скорость электронов не зависит от температуры, т.к. уровень Ферми (энергия Ферми EF) не изменяется.
С ростом температуры усиливаются тепловые колебания атомов в узлах кристаллической решетки.
Поэтому увеличивается рассеяние электронных волн на решетке, уменьшается средняя длина пробега молекул , т.к. она обратно пропорциональна температуре
~ .
Уменьшение длины свободного пробега приводит в соответствии с формулой (22.3.1) к уменьшению проводимости значит, сопротивление металла возрастает. Таким образом получаем: сопротивление металла пропорционально его температуре в первойстепени Т, что совпадает с экспериментом.
Сверхпроводимость
При низких температурах у металлов наблюдается сверхпроводимость (сопротивление становится равным нулю). Явление сверхпроводимости открыл Г. Камерлинг-Оннес в 1911 году (нобелевская премия 1913 г.). Он наблюдал уменьшение до нуля сопротивления ртути при температуре Тс = 4,1 К (рис. 22.4.1).
- Сверхпроводимость наблюдается у ртути, алюминия, олова, свинца, таллия и др.
- При сверхпроводимости ток может идти миллионы лет.
- Для золота, серебра, платины, меди, щелочных и щелочноземельных элементов, ферромагнетиков сверхпроводимость не наблюдается.
Квантовую теорию сверхпроводимости разработали Д. Бардин, Л. Купер и Д. Шриффер в 1957 г. (нобелевская премия 1972 г.).
При сверхпроводимости магнитное поле в проводник равно нулю, т.е. оно вытесняется из сверхпроводника. Это явление называется эффект В. Мейснера (1933 г.). Сверхпроводник является идеальным диамагнетиком с магнитной проницаемостью равной нулю μ = 0.
Сверхпроводимость получают двумя способами.
1. Подключают металл в электрическую цепь, а затем его температуру уменьшают до критической, когда наступает сверхпроводимость. Падение напряжения на сверхпроводнике становится равным нулю.
2. Во втором способе кольцо из сверхпроводника охлаждают до критической температуры и помещают в магнитное поле, которое затем выключают. Электромагнитная индукция приводит к возникновению тока.
Сильное магнитное поле или сильный ток разрушают сверхпроводимость.
По квантовой теории сверхпроводимости электроны тока деформируют кристаллическую решетку, т.е. смещают положительно заряженные узлы решетки.
В результате кроме кулоновских сил отталкивания между двумя электронами появляются силы притяжения и возникают куперовские пары. Размер куперовской пары составляет несколько межатомных расстояний. Спины электронов куперовской пары направлены противоположно, поэтому спин такой системы равен нулю.
Куперовская пара является бозоном. Эти пары движутся в металле без сопротивления, наблюдается сверхпроводимость. При температуре выше критической температуры энергии теплового движения становится достаточно для разрушения куперовских пар, появляется сопротивление.
В 1986 г. Дж. Беднорц и К. Мюллер открыли высокотемпературную сверхпроводимость у металлооксидных керамик при Т = 35 К (нобелевская премия 1987 г.).
Металлооксидные керамики изготовляют в лаборатории, в природе их нет. При температуре выше критической они могут проявлять свойства полупроводников или диэлектриков.
Сверхпроводимость удается получать при температуре 138 К, а при высоких давлениях даже при 166 К.
Эффект Джозефсона
В 1962 г. Б. Джозефсон предсказал явление, которое назвали эффектом Джозефсона (нобелевская премия 1973 г.).
В электрическую цепь с постоянной ЭДС включают два сверхпроводника, разделенных диэлектриком толщиной 1 нм. Ток проходит через диэлектрик. Это явление называется эффектом Джозефсона. Электроны проходят через диэлектрик благодаря туннельному эффекту.
Различают стационарный и нестационарный эффекты Джозефсона.
А. При стационарном эффекте, когда сила тока не больше критического значения I ≤ Iкр, падение напряжения на контакте (диэлектрике) равно нулю.
Из соотношения = 0 следует, что сопротивление равно нулю, т.е. наблюдается сверхпроводимость.
Б. Эффект называется нестационарным, когда сила тока больше критического значения I > Iкр. В контакте возникает падение напряжения U, и контакт излучает электромагнитные волны.
- Механизм излучения заключается в следующем.
- При сверхпроводимости электроны образуют куперовские пары.
- Эта пара зарядов проходит через контакт и получает дополнительную энергию . Возвращаясь в основное состояние, куперовская пара излучает полученную ранее энергию в виде кванта электромагнитной волны
- .
- Частота излучения равна
- .
- Коэффициент «2» в эффекте Джозефсона доказывает существование куперовских пар при сверхпроводимости.
- Эффект Джозефсона применяют для точного измерения очень слабых магнитных полей (10-18 Тл), токов (10-10А) и напряжений (10-15В).
- Лекция 23
Понятие о квантовой теории электропроводности металлов
Теория электропроводности металлов, построенная на основе квантовой механики и квантовой статистики Ферми-Дирака, называется квантовой теорией электропроводности металла.
Расчет электропроводимости металлов в квантовой теории был произведен Зоммерфельдом. Был выведен закон Ома в дифференциальной форме
где g — удельная проводимость; — плотность тока в данной точке; — напряженность электрического поля.
Для удельной проводимости было получено следующее выражение:
где — средняя длина свободного пробега электрона, обладающего энергией Ферми, — скорость такого электрона, m — его масса.
Сравним (3.12) с выражением, полученным из классической электронной теории металлов
В этом выражении — средняя длина свободного пробега электрона, — средняя скорость его теплового движения.
Несмотря на то, что выражения (3.12) и (3.13) по внешнему виду похожи, их содержание различно. Средняя скорость теплового движения зависит от температуры, как , а практически не зависит от температуры, так как с изменением температуры энергия Ферми, а, следовательно, и скорость, остаются практически неизменными.
Наиболее существенное различие формул (3.3.2) и (3.3.3) состоит в том, какой смысл вкладывается в понятие длины свободного пробега электрона в классической и квантовой теории металлов.
Классическая электронная теория рассматривает электроны как обычные частицы и причиной электрического сопротивления металлов считает столкновения электронов с узлами кристаллической решетки. Полагая, что электроны сталкиваются почти со всеми узлами решетки, встречающимися на их пути, классическая теория принимает равной параметру решетки d (d »10-10 м).
Квантовая теория рассматривает электрон как частицу, обладающую волновыми свойствами, а электрический ток в металле — как процесс распространения электронных волн, длина волны которых определяется формулой де Бройля
. (3.3.4)
Такие представления позволяют объяснить наблюдаемую экспериментально температурную зависимость удельной проводимости g и удельного сопротивления .
Рассмотрим идеальную кристаллическую решетку металла, в узлах которой находятся неподвижные ионы, а примеси и дефекты отсутствуют.
Такая идеальная решетка не рассеивает электронные волны, и электрическое сопротивление такого металла должно быть равно нулю.
В реальных кристаллах при T > 0 ионы совершают тепловые колебания около положения равновесия, нарушая строгую периодичность решетки.
Кроме того, в таких решетках обычно присутствуют структурные дефекты: примеси, вакансии, дислокации и так далее.
Все эти неоднородности играют роль центров рассеивания для электронных волн и являются причиной электрического сопротивления. Расчет показывает, что средняя длина свободного пробега зависит от температуры по закону
, (3.3.5)
где — модуль упругости; d — параметр решетки.
С учетом (3.15) удельная проводимость g, определяемая формулой (3.12), будет иметь вид
, (3.3.6)
то есть ~ , а ~ , что хорошо согласуется с опытом в области не слишком низких температур.
При очень низких температурах формула (3.3.5) не выполняется. При этом длина свободного пробега оказывается обратно пропорциональной не первой, а пятой степени температуры, поэтому и удельное сопротивление ρ будет пропорционально пятой степени абсолютной температуры.
На рис.3.7 изображена зависимость удельного электрического сопротивления металла от температуры. При Т=0 удельное сопротивление металла равно не нулю, а остаточному сопротивлению rост,, обусловленному рассеиванием электронных волн на структурных дефектах решетки металла.
Физики смоделировали поведение странных металлов
Cha Peter et al. / Proceedings of the National Academy of Sciences, 2020
Американские
физики создали решеточную модель, в которой им удалось воспроизвести реальную температурную
зависимость удельного сопротивления странных металлов. В отличие от обычных
металлов, в их странных аналогах, которые также называют планковскими, сопротивление
пропорционально температуре вблизи абсолютного нуля.
Добиться описания этого явления исследователям удалось с
помощью моделирования переходов между тремя состояниями вещества: спиновым стеклом, ферми-жидкостью и изолятором Мотта.
С развитием вычислительных
методов созданная модель позволит лучше понять физику странных металлов и
приблизиться к описанию высокотемпературной сверхпроводимости, пишут авторы в журнале Proceedings of the National Academy of Sciences.
Название
странных металлов уже само по себе говорит о степени их изученности. Это состояние вещества
можно назвать промежуточным между проводником и диэлектриком: в нем электроны
уже свободны, однако все еще существенно менее подвижны, чем в обычном металле.
При этом в планковских металлах наблюдается максимально допустимый квантовой
механикой темп диссипации энергии.
Такое поведение проводящих электронов
приводит к необычной температурной зависимости удельного сопротивления: вблизи абсолютного
нуля оно пропорционально температуре, в то время как у обычных металлов, как
правило, после сверхпроводящей фазы идет более резкий рост сопротивления.
Особенно интересна
линейная зависимость удельного сопротивления от температуры из-за того, что она характерна
для купратов — веществ с крайне высокими температурами сверхпроводимости при
нормальном давлении, которые также являются странными металлами.
Существует ряд статистических моделей, которые в первом
приближении описывают такое поведение удельного сопротивления, но у ученых долго
не получалось создать достаточно полную микроскопичную теорию.
Феноменология
купратов мотивировала и рождение теорий о квантовой спиновой жидкости (про то,
что это такое, мы достаточно подробно писали в материале «Квантовая азбука:
Спиновая жидкость»).
Так как особое поведение странных металлов дает о себе
знать вблизи абсолютного нуля, физики стали изучать основные состояния (стационарные
состояния при нуле энергии) квантовых систем в рамках подобных теорий. Однако, хоть такой подход и демонстрировал требуемую температурную зависимость
удельного сопротивления, основным состоянием вещества в этих моделях оказалось
спиновое стекло, а не планковский металл.
Спиновое
стекло, в свою очередь — это класс веществ, в которых отдельные магнитные моменты
атомов расположены хаотично. Из названия видна параллель с обычным стеклом, в
котором аморфно распределены сами атомы, входящие в его состав.
Однако природа
аморфности магнитных моментов в спиновом стекле гораздо сложнее и возникает
из-за РККИ-обменного взаимодействия, которое осуществляется между магнитными
ионами через коллективизированные электроны проводимости.
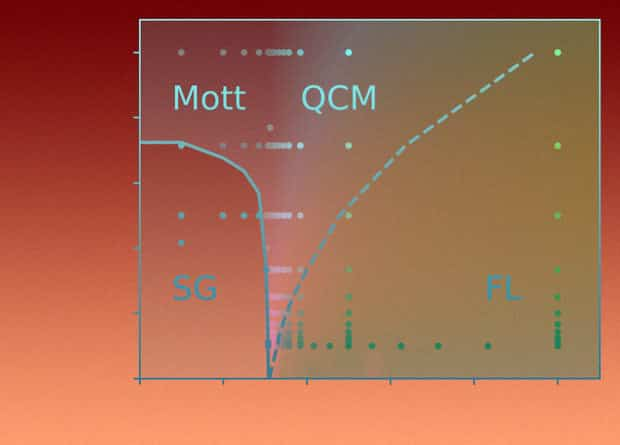
На фазовых диаграммах
спиновое стекло часто соседствует с ферми-жидкостью — низкотемпературной квантовой жидкостью взаимодействующих фермионов
(частиц с полуцелым спином), обладающей трансляционной
инвариантностью. Именно с помощью теории ферми-жидкости описывается поведение
электронов в обычных металлах при низких температурах.
Теперь Питер Ча (Peter
Cha) из Корнельского университета и его коллеги определили, что электроны в странных металлах
по своей природе являются чем-то промежуточным между электронами в
спиновом стекле и в ферми-жидкости.
Оказалось, что между этими двумя
состояниями существует квантовая критическая точка (критическая точка между
двумя состояниями вещества при абсолютном нуле температур), и именно в ней удельное
сопротивление в веществе оказывается пропорционально температуре.
При повышении
температур характерная странным металлам температурная зависимость обнаруживается в веществах, расположенных на фазовой диаграмме в области между ферми-жидкостью и изолятороми Мотта.
Последние представляют собой кристаллические вещества с диэлектрическими
свойствами, которые могли бы быть проводниками согласно обычной теории
электрической проводимости, но в реальности являются изоляторами из-за мешающего
перемещению заряда кулоновского отталкивания между электронами.
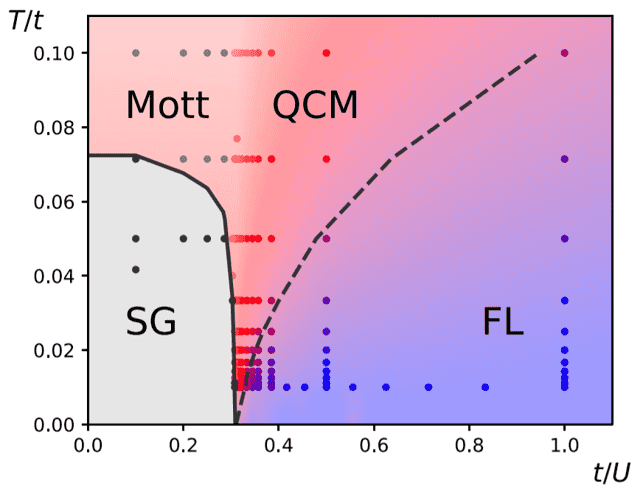
Вычисленная с помощью модели фазовая диаграмма. SG — спиновое стекло, Mott — изолятор Мотта, FL — ферми-жидкость. QCM соответствует металлу со спиновой динамикой, характерной для квантовой спиновой жидкости
Cha Peter et al. / Proceedings of the National Academy of Sciences, 2020
В своей
работе физики описывают реализованную ими решетчатую
модель, позволяющую симулировать процесс «плавления» спинового стекла за счет
квантовых флуктуаций заряда внутри вещества, в результате которого физики получили
планковский металл со всеми присущими ему свойствами.
В рамках модели исследователи
описывали взаимодействие электронов в кристаллической решетке с помощью модели
Хаббарда, а также внедряли в симуляцию спин-спиновое взаимодействие с
бесконечным радиусом действия.
Такой микроскопичный подход к моделированию плохо
сказывался на скорости вычисления, что в сочетании с квантовой связанностью всех взаимодействующих
электронов не позволяло моделировать всю систему целиком.
Для решения этой
проблемы авторы использовали квантовый метод вложений, который позволяет
подробно моделировать лишь небольшой участок исследуемой материи, одновременно упрощая
вычисления для остальной системы. Вместе с использованием квантового
метода Монте-Карло для генерации произвольных начальных условий системы это
позволило ученым добиться описанных выше результатов.
Более того,
авторы отмечают, что в процессе моделирования система приобретала локальную спиновую
динамику, характерную для семейства SYK-моделей. Такие модели используются для моделирования не
только процессов в черных дырах, но и квантовых спиновых жидкостей, и, как упоминалось выше, раньше
их пытались использовать для моделирования странных металлов.
Такое совпадение результатов
микроскопичного моделирования с более общими теориями может говорить о потенциале
последних в исследовании планковских металлов. Кроме того, современные
возможности вычислительных комплексов не дали исследователям вплотную подойти к
абсолютному нулю температур.
Ученые надеются, что с развитием вычислительной
техники их модель сможет дать еще более интересные результаты.
Свойства
странных металлов наблюдаются
и в повернутом под определенным углом двухслойном графене. Про фундаментальные
открытия в физике конденсированного состояния, которые положили начало
исследованиям сверхтекучести и высокотемпературной сверхпроводимости, можно почитать
в нашем материале «Чашка жидкого гелия».
Никита Козырев
Квантовая теория электропроводности металла
Процесс электропроводности металлов возможно рассмотреть с квантовой точки зрения.
Известно, что при объединении атомов в определенную кристаллическую решетку наблюдается постепенное снижение высоты всех стенок основного барьера, расположенного вокруг ядра каждого атома.
При этом динамично движущиеся валентные электроны начинают перемещаться по всему кристаллу, а элементы внутренних оболочек не покидают своих позиций и остаются на своих местах.
Рисунок 1. Электропроводимость металлов. Автор24 — интернет-биржа студенческих работ
Определение 1
Квантовая теория электропроводности металлов — гипотеза электропроводности, которая основывается на принципах квантовой механики и статистике Ферми — Дирака.
Такое предположение отодвинуло закон Больцмана на последнее место, так как его теория была абсолютно не применима к электронам проводимости металла.
На самом деле, указанный закон гласит, что общее количество частиц газа, которые находятся в состоянии равновесия, определяется формулой, не имеющей никаких ограничений на число электронов.
Все элементы этой системы должны иметь нулевую энергию.
Согласно научной работе Паули, каждый подуровень в электропроводности металлов может содержать только два электрона. Таким образом, надо отказаться от учений Больцмана и найти для электронов проводимости иной статистический закон.
Сверхпроводимость металлов в квантовой физике
В сфере действия низких температур возникает процесс сверхпроводимости в виде резкого падения общего сопротивления материала. Впервые данное явление было обнаружено в начале 1911 года Камерлингом-Оннесом для определения значения ртути при температуре 4.2 К.
Экспериментально сверхпроводимость металлов осуществляется двумя способами:
- включив в металлическую цепь звено из сверхпроводника, где в момент перехода в сверхпроводящее условие отличие потенциалов на концах каждого участка будет равна нулю;
- разместив кольцо из сверхпроводника в параллельное к нему электромагнитное поле и охладив элемент ниже температуры перемещения в сверхпроводящее состояние, выключают поле.
В итоге в кольце начинает постепенно индуцироваться незатухающий электрический ток, циркуляция которого может длиться бесконечно долго. Такой научный эксперимент подтвердил, что кольцо необходимо поддерживать при определенной температуре, в результате чего ток в нем будет наблюдаться как минимум в течение двух лет.
Замечание 1
Для сверхпроводящего состояния вещества, кроме отсутствия электрического сопротивления, присущ так называемый принцип Мейснера: вытеснение магнитного поля из общего объема действующего проводника.
Теория сверхпроводимости металлов была представлена общественности и научному миру в 1957 году Купером, Бардиным и Шиффером. Проведенные на сегодняшний день экспериментальные исследования только подтверждают эту гипотезу.
Основная суть ее состоит в следующем: в металле между электронами появляется особый вид напряжение, помимо интенсивности работы кулоновского отталкивания. При крайне низких температурах эта гравитация оказывается значительно сильнее самого отодвигания.
В итоге все свободные электроны объединяются в куперовские пары, представляющие собой бозон.
Распределение Ферми-Дирака
При температуре абсолютного нуля в каждом из возможных состояний, энергия которых ниже силы Ферми для определенного металла, можно обнаружить один электрон; в самих процессах электронов нет. Поэтому функция группирования электронов по энергиям равняется вероятности пребывания элемента в состоянии с конкретной энергией.
Для того, чтобы обнаружить эту функцию при температуре выше абсолютного нуля, необходимо изучить неупругие соединения электрона с атомом, расположенном в стабильном узле кристаллической решетки.
Вероятность столкновения электронов, в результате которого элемент трансформируется в состояние с энергией, а атом – в положение с нулевой энергией, пропорциональна:
- возможности пребывания электрона в состоянии с теплоэнергией;
- допустимость того, что положение электрона в атоме свободно;
- вероятности того, что атом металла находится в том же энергетическом состоянии.
Обратный процесс может возникнуть, если энергия атома начнет уменьшаться, а сила электрона увеличиваться при пребывании данного элемента в состоянии с нулевой энергией. Следовательно, в металлах средняя активность теплового движения электронов равна общей энергии Ферми, которая поглощается при температурах примерно 30000 К.
Поэтому коэффициент температуры плавления электронного газа в металлах можно считать вырожденным, так как в проводимых металлах концентрация свободных электронов будет значительно меньше, чем в других материалах. Из этого получается, что уже при комнатной температуре в полупроводниках электронный газ будет невырожденным, полностью подчиняющимся закону Больцмана.
Движение электронов в кристаллической решетке
В кристаллической решетке все неподвижные частицы отсутствуют из-за нарушения периодичности, поэтому электроны ведут себя аналогично оптически однородной среде, которая не распределяет «электронные волны». Это соответствует тому, что металлические элементы не оказывают никакого сопротивления электрическому току.
Замечание 2
В действительной кристаллической решетке часто имеются неоднородности, которыми могут быть разнообразные примеси, обусловленные тепловыми колебаниями.
В указанной среде происходит частичное рассеяние «электронных волн» на разнообразии элементов, что и является причиной стабильного электрического сопротивления металлов. Распределение электронных частиц на неоднородностях можно рассматривать как абордаж электронов с фононами.
В квантовой теории средняя скорость практически не зависит от температуры, так как с изменением этого коэффициента уровень Ферми остается неизменным.
Однако с увеличением градуса рассеяние «электронных волн» на всех тепловых колебаниях решетки постепенно возрастает, что автоматически провоцирует уменьшение средней длины свободного фонона.
При комнатных температурах в результате сопротивления металлов температура будет расти пропорционально. Таким образом, квантовая гипотеза электропроводности металлов смогла устранить эту трудность классической теории.
Простейшая квантовая теория электропроводности металлов
В пределах квантово-механической теории перемещение электронов в металле представляет собой распространение их дебройлевских волн.
При этом свет проходит исключительно через мутную среду и определяет сам процесс рассеяния, которое приводит к уменьшению интенсивности определенного пучка.
Для возникновения распределения энергии необходимо, чтобы все частицы макросреды находились на расстояниях, сравнимых с длиной волны.
Длина дебройлевской волны электрона всегда участвует в токе проводимости.
Расчеты ученых показывают, что общая скорость стабильного движения электронов в конкретном металлическом проводнике характеризуется величиной примерно в 0,1 мм/с.
Определив количественные значения в формулу можно определить, что длина волны равняется приблизительно 7 м. другими словами, металлический проводник с наилучшей кристаллической решеткой не обладает электрическим сопротивлением.
Нарушение установленной и строгой периодичности размещения атомов напрямую связано с различного рода изъянами – вакансиями, бесконтрольными примесями других химических элементов, дислокациями и многочисленными тепловыми колебаниями атомов.
Следует иметь в виду, что в классической теории электрическое внешнее поле приводит в урегулирование движение все свободные элементы металла, в то время как в квантовой гипотезе ток проводимости возникает только при действии тех электронов, энергия которых близка к уровню Ферми.
3.6. Понятие о квантовой теории электропроводности металлов
Электрический ток в металлах – результат
упорядоченного движения электронов.
Электрическое сопротивление как в
классической, так и в квантовой теории
объясняется взаимодействием электронов
проводимости с кристаллической решёткой,
при котором электроны теряют часть
своей энергии. Но характер взаимодействия
в классической и квантовой теории рассматривается различным образом.
По классической теории:электроны
сталкиваются с узлами кристаллической
решетки и отдают ей часть своей энергии
– этим обусловлено электрическое
сопротивление металлов. Классическая
теория принимает длину свободного
пробега электроновравной параметру решеткиd(d10-10м).
По квантовой теории:электроны
обладают волновыми свойствами, а их
упорядоченное движение рассматривается
как процесс распространения электронных
волн де Бройля в периодической среде. Длина волны де Бройля определяется
известной формулой:
Электрическое
сопротивление объясняется рассеиванием
электронных волн.
Рассеивание электронных волн происходит
лишь на искажениях периодичности
решётки. Такие искажения периодичности
возникают в реальных кристаллах
- за счёт тепловых колебания узлов решётки около положения равновесия при T > 0;
- за счёт структурных дефектов: примесных атомов, вакансий, дислокаций и так далее.
- Все эти неоднородности играют роль центров
рассеивания электронных волн и являются
причиной электрического сопротивления. -
Теория электропроводности металлов,
построенная на основе квантовой механики
и квантовой статистики Ферми-Дирака,
называется квантовой теорией
электропроводности металла. -
Расчет электропроводимости металлов
в квантовой теории был произведен
Зоммерфельдом. Был выведен закон Ома в
дифференциальной форме
где —
удельная проводимость;- плотность тока в данной точке;- напряженность электрического поля.
Для удельной проводимости было получено
следующее выражение:
Здесь — средняя длина свободного пробега
электрона, обладающего энергией Ферми,- скорость этого электрона,m— его масса.
Сравним (3.12) с выражением, полученным
из классической электронной теории
металлов:
В этом выражении
— средняя длина свободного пробега
электрона,- средняя скорость его теплового движения.
Несмотря на то, что выражения (3.12) и (3.13) по внешнему виду похожи, их содержание
различно. Средняя скорость теплового
движения
png» width=»44″>пропорциональна корню квадратному из
абсолютной температуры,
а
png» width=»52″>практически не зависит от температуры,
так как с изменением температуры энергия
Ферми, а следовательно, и скорость
остаются практически неизменными.
-
Такие
представления позволяют объяснить
наблюдаемую экспериментально температурную
зависимость удельной проводимостии удельного сопротивления: - ,,
- что хорошо
согласуется с опытом в области не слишком
низких температур.
На рис.3.6 изображена зависимость удельного
электрического сопротивления металла
от температуры. При Т=0удельное
сопротивление металла равно не нулю, а
остаточному сопротивлениюост
,обусловленному рассеиванием
электронных волн на структурных дефектах
решетки металла.