- Формула Ньютона-Рихмана
- Дифференциальное уравнение теплоотдачи
- Критерий Нуссельта
- Коэффициент теплоотдачи и его связь с коэффициентом теплопередачи
- Единицы измерения
- Примеры решения задач
- Коэффициент теплоотдачи поверхность — воздух
- Схемы теплообмена:
- Расчет в Excel:
- Замечание:
- Литература:
- P. S. (01.11.2020)
- Дополнение по естественной конвекции у вертикальной поверхности:
- Коэффициенты теплопередачи сталей и других материалов: факторы, влияющие на теплопроводность сплавов
- Понятие теплопроводности
- Перенос тепла на молекулярном уровне
- Теплопроводность материалов
- Коэффициенты теплопередачи сталей
- Факторы, влияющие на физическую величину
- Температура материала
- Фазовые переходы и структура
- Электрическая проводимость
- Процесс конвекции
- Теплоотдача 1 м стальной трубы – проводим расчет
- Для каких систем нужен расчёт?
- Как оптимизировать теплоотдачу стальной трубы?
- Производим расчёт
- Рассчитываем отдачу для 1 м. изделия
- Об этом стоит помнить
- Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах
- Теплоотдача при вынужденном течении жидкости в трубах и каналах
- Теплоотдача при ламинарном течении в трубах и каналах
- Теплоотдача при свободной конвекции в трубах и каналах
- Свободная конвекция в неограниченном пространстве
- Свободная конвекция в ограниченном объеме
Конвективный теплообмен — обмен теплотой между частями жидкости (газа), имеющими разную температуру или между жидкостью (газом) и твердым телом. Конвективный теплообмен между жидкостью и твердым телом называют теплоотдачей.
Этот коэффициент часто используют в гидроаэродинамике, когда исследуют конвективный теплообмен. Часто ее обозначают буквой . Коэффициент равен:
где — плотность теплового потока, — температурный напор. Величина q — это количество теплоты, которое передается через единичную площадь поверхности тела в единицу времени. находят как модуль разности температур жидкости и поверхности тела.
Иногда температурный напор находят, например, в случае обтекания тела потоком сжимаемой жидкостью, считают равным модулю разности температуры жидкости далеко от тела и температурой поверхности тела, которая была бы в отсутствии теплообмена.
Коэффициент теплоотдачи зависит от скорости потока носителя тепла, вида течения, какова геометрия поверхности твердого тела и т.д. Это сложная величина и ее невозможно определить общей формулой. Обычно коэффициент теплоотдачи находят экспериментально.
Так, для условий свободной конвекции воздуха: (Вт/м2К), воды: (Вт/м2К). При вынужденной конвекции величины коэффициента теплоотдачи колеблются в пределах: для воздуха: (Вт/м2К), для воды: (Вт/м2К).
Формула Ньютона-Рихмана
Коэффициент теплоотдачи входит в выражение для потока тепла в веществе жидкой или газообразной среды с интенсивным изменением температуры при увеличении расстояния от охлаждаемого или нагреваемого объекта:
где — количество теплоты, которая отводится от поверхности, имеющую площадь S, — температура вещества (жидкости, газа), — температура поверхности тела. Выражение (2) называется формулой Ньютона — Рихмана.
- Так как интенсивность теплообмена может изменяться при передвижении вдоль площади соприкосновения жидкого носителя с поверхностью твердого тела, вводят местный коэффициент теплоотдачи, который равен:
- На практике чаще применяют средний коэффициент теплоотдачи , вычисляя его по формуле:
- где температуры берут средние для поверхности и для вещества.
Дифференциальное уравнение теплоотдачи
Дифференциальное уравнение теплоотдачи показывает связь между коэффициентом теплоотдачи и полем температур среды (жидкости или газа):
Критерий Нуссельта
- Критерий Нуссельта () является характеристикой теплообмена на границе между жидкостью и стеной:
- где — характерный линейный размер, — коэффициент теплопроводности жидкости. Для стационарного процесса критерий Нуссельта находят, используя критериальное уравнение конвективного теплообмена:
где постоянные. — критерий Рейнольдса, — критерий Прандтля, — критерий Грасгофа.
Коэффициент теплоотдачи и его связь с коэффициентом теплопередачи
- Коэффициентом теплопередачи через плоскую стенку связан с коэффициентами теплоотдачи выражением:
- где — коэффициент теплоотдачи от первой среды к стенке, — коэффициент теплоотдачи от стенки ко второй среде, — толщина стенки, — коэффициент теплопроводности стенки.
Единицы измерения
Основной единицей измерения коэффициента теплоотдачи в системе СИ является:
=Вт/м2К
Примеры решения задач
| Понравился сайт? Расскажи друзьям! |
Коэффициент теплоотдачи поверхность — воздух
Опубликовано 06 Апр 2020Рубрика: Теплотехника | 16 комментариев
Зная коэффициент теплоотдачи на поверхности (α), разделяющей твердое тело и окружающее это тело воздушное пространство, очень просто определить мощность теплового потока (Q) по известной разности температур (Δt).
Q=α*A*Δt, Вт – мощность теплового потока от или к поверхности тела.
- α=αк+αр, Вт/(м2*К) – суммарный коэффициент теплоотдачи на границе воздух – поверхность тела
- αк=?, Вт/(м2*К) – коэффициент конвективной теплоотдачи
- αр=ε*5,67*10-8*((tп+273,15)4— (tв+273,15)4)/(tп-tв)), Вт/(м2*К) – коэффициент радиационной теплоотдачи (теплоотдачи излучением), ε – степень черноты поверхности
- А, м2 – площадь поверхности
- Δt=|tп-tв|, К – разность температур поверхности и воздушной среды
- tп, °C – температура поверхности
- tв, °C – температура воздуха
Основная сложность расчета заключается в определении коэффициента конвективной теплоотдачи (αк)! Автоматизировать в первую очередь решение этой трудоемкой задачи поможет Excel.
Нестабильность процесса естественной конвекции у поверхностей различной формы и расположения в пространстве породила большое разнообразие эмпирических формул для вычисления коэффициента конвективной теплоотдачи (αк). Неизбежные погрешности экспериментальных данных привели к тому, что результаты вычислений для одних и тех же поверхностей и условий по формулам разных авторов отличаются друг от друга на 20% и более.
После тщательного детального ознакомления с материалами современных западных изданий по теплообмену (список литературы – в конце статьи) были выбраны формулы, рекомендованные к применению большинством авторов, для использования в представленной далее программе в Excel.
Схемы теплообмена:
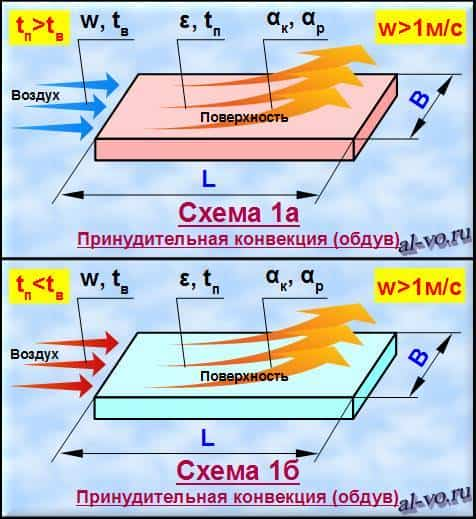
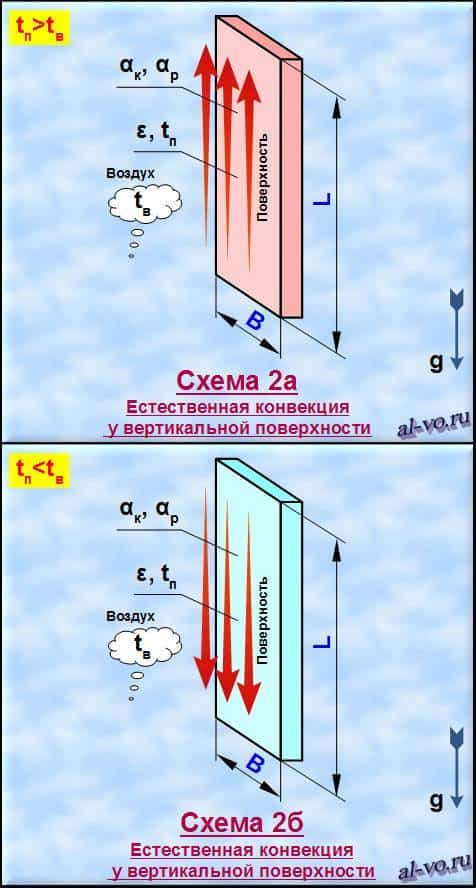
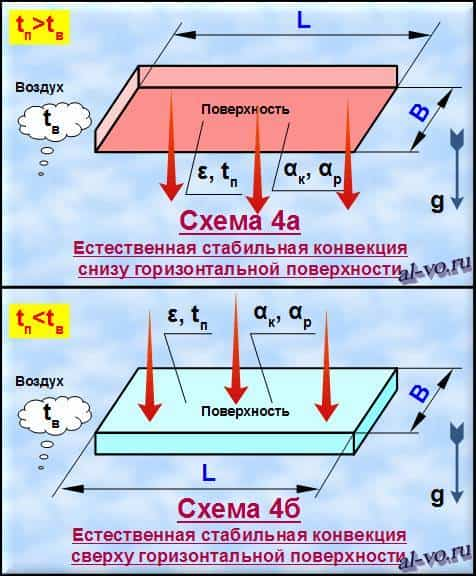
На представленных ниже рисунках показаны 8 вариантов схем, для которых программа может выполнить вычисления.
Розовый цвет пластин свидетельствует о том, что они горячее окружающего воздуха. Голубой цвет – пластины холоднее воздуха.
На схемах 1а и 1б воздух принудительно движется (вентилятор, ветер) вдоль поверхности пластины независимо от её ориентации в пространстве. На всех остальных схемах окружающий воздух находится в спокойном состоянии (помещение, полный штиль), а положение пластин сориентировано в пространстве.

Расчет в Excel:
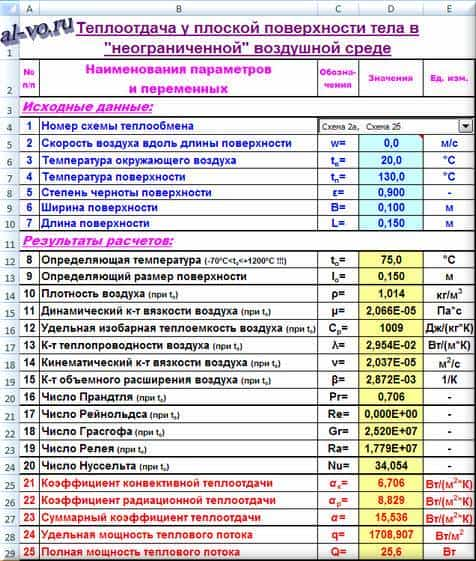
- Формулы алгоритма программы:
- t=(tв+tп)/2
- l=L – для схем 1а и 1б
- l=(B*L)/(2*(B+L)) – для схем 2а, 2б, 3а, 3б, 4а, 4б
- Для определения теплофизических параметров воздуха при определяющей температуре (t0) в диапазоне -70°C … +1200°C использованы формулы из предыдущей статьи на сайте.
- Re=w*l/ν
- Gr=g*β*|tп— tв|*l3/ν2
- Ra=Gr*Pr

- αк=Nu*λ/l
- αр=ε*0,00000005670367*((tп+273,15)4— (tв+273,15)4)/(tп-tв)) – при tвtп
- α=αк+αр
- q=α*(tп-tв)
- Q=q*B*L
- *)Нагрев поверхностей Солнцем или иными источниками теплового излучения программой игнорируется.
- Вычисление теплофизических параметров воздуха и числа Нуссельта, как видно из вышеприведенных формул, являются ключевыми и самыми трудоемкими при определении конвективного коэффициента теплоотдачи.
Тестирование программы проводилось на примерах из книг, представленных в конце статьи. Отклонения результатов в основном не выходили за пределы ±5%.
Замечание:
В отечественной теплотехнической литературе для решения рассмотренных задач широко используются формулы второй половины прошлого века М.А. Михеева и В.П. Исаченко, которые в современной западной литературе не упоминаются.
Беглый сравнительный анализ результатов расчетов по формулам разных авторов дал противоречивые и неоднозначные ответы.
Если при принудительной конвекции результаты фактически идентичны, то при естественной конвекции отличаются порой на 30% и более, но иногда почти совпадают…
Литература:
- John H. Lienhard IV, John H. Lienhard V, A Heat Transfer Textbook (Fifth Edition), 2019.
- Frank Kreith, Raj M. Manglik, Mark S. Bohn, Principles of heat transfer (Seventh Edition), 2011.
- Adrian Bejan, Convection Heat Transfer (Fourth Edition), 2013.
- Michel Favre-Marinet, Sedat Tardu, Convective Heat Transfer, 2009.
- Harlan H. Bengtson, Convection Heat Transfer Coefficient Estimation, 2010.
- Rajendra Karwa, Heat and Mass Transfer, 2017.
- Stuart W. Churchill, Humbert H. S.
Chu, Correlating equations for laminar and turbulent free convection from a vertical plate, International Journal of Heat and Mass Transfer, Volume 18, Issue 11, November 1975.
- http://people.csail.mit.edu/jaffer/SimRoof/Convection/
- И. И. Кирвель, М. М. Бражников, Е. Н. Зацепин ЭНЕРГОСБЕРЕЖЕНИЕ В ПРОЦЕССАХ ТЕПЛООБМЕНА, 2007.
Прошу уважающих труд автора скачать файл с программой после подписки на анонсы статей!
Ссылка на скачивание файла: koehfficient-teplootdachi-poverhnost-vozduh (xlsx 225KB).
P. S. (01.11.2020)
Дополнение по естественной конвекции у вертикальной поверхности:
Если построить графики по вышеприведенным формулам Черчилля и Чу для числа Нуссельта при естественной конвекции у вертикальной изотермической поверхности (схемы 2а и 2б), то можно увидеть, что при Ra=109 кривые не совпадают!
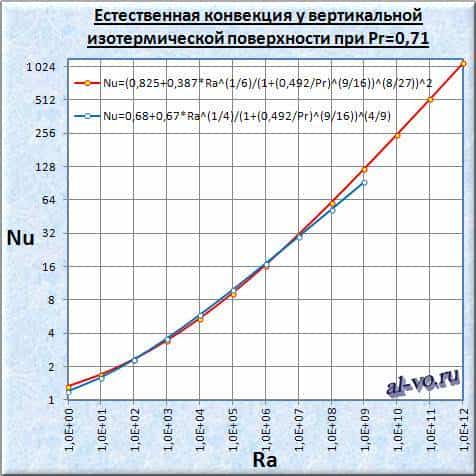
По этому поводу авторы формул Черчилль и Чу дают примерно следующее пояснение: «уравнение, основанное на исследованиях Черчилля и Усаги Nu=(0,825+0,387*Ra1/6/(1+(0,492/Pr)9/16)8/27)2 дает хорошие результаты для средней теплопередачи при свободной конвекции у изотермической вертикальной пластины во всем диапазоне значений Ra и Pr от до ∞, даже если оно не работает для обозначения дискретного перехода от ламинарного к турбулентному потоку». Линхарды в [1] отмечают, что рассматриваемое уравнение чуть менее точно для ламинарных условий при Ra
Коэффициенты теплопередачи сталей и других материалов: факторы, влияющие на теплопроводность сплавов
Теплопроводность представляет собой физическую величину, которая определяет способность материалов проводить тепло.
Иными словами, теплопроводность представляет собой способность субстанций передавать кинетическую энергию атомов и молекул другим субстанциям, находящиеся в непосредственном контакте с ними.
В СИ эта величина измеряется во Вт/(К*м) (Ватт на Кельвин-метр), что эквивалентно Дж/(с*м*К) (Джоуль на секунду-Кельвин-метр).
Понятие теплопроводности
Она является интенсивной физической величиной, то есть величиной, которая описывает свойство материи, не зависящей от количества последней. Интенсивными величинами также являются температура, давление, электропроводность, то есть эти характеристики одинаковы в любой точке одного и того же вещества. Другой группой физических величин являются экстенсивные, которые определяются количеством вещества, например, масса, объем, энергия и другие.
Противоположной величиной для теплопроводности является теплосопротивляемость, которая отражает способность материала препятствовать переносу проходящего через него тепла. Для изотропного материала, то есть материала, свойства которого одинаковы во всех пространственных направлениях, теплопроводность является скалярной величиной и определяется, как отношение потока тепла через единичную площадь за единицу времени к градиенту температуры. Так, теплопроводность, равная одному ватту на метр-Кельвин, означает, что тепловая энергия в один Джоуль переносится через материал:
- за одну секунду;
- через площадь один метр квадратный;
- на расстояние один метр;
- когда разница температур на поверхностях, находящихся на расстоянии один метр друг от друга в материале, равна один Кельвин.
Понятно, что чем больше значение теплопроводности, тем лучше материал проводит тепло, и наоборот. Например, значение этой величины для меди равно 380 Вт/(м*К), и этот металл в 10 000 раз лучше переносит тепло, чем полиуретан, теплопроводность которого составляет 0,035 Вт/(м*К).
Перенос тепла на молекулярном уровне
Когда материя нагревается, увеличивается средняя кинетическая энергия составляющих ее частиц, то есть увеличивается уровень беспорядка, атомы и молекулы начинают более интенсивно и с большей амплитудой колебаться около своих равновесных положений в материале. Перенос тепла, который на макроскопическом уровне можно описать законом Фурье, на молекулярном уровне представляет собой обмен кинетической энергией между частицами (атомами и молекулами) вещества, без переноса последнего.
Это объяснение механизма теплопроводности на молекулярном уровне отличает его от механизма термической конвекции, при котором имеет место перенос тепла за счет переноса вещества.
Все твердые тела обладают способностью к теплопроводности, в то время как тепловая конвекция возможна только в жидкостях и газах.
Действительно, твердые вещества переносят тепло в основном за счет теплопроводности, а жидкости и газы, если есть температурные градиенты в них, переносят тепло в основном за счет процессов конвекции.
Теплопроводность материалов
Ярко выраженной способностью проводить тепло обладают металлы. Для полимеров свойственна невысокая теплопроводность, а некоторые из них практически не проводят тепло, например, стекловолокно, такие материалы называются теплоизоляторами. Чтобы существовал тот или иной поток тепла через пространство, необходимо наличие некоторой субстанции в этом пространстве, поэтому в открытом космосе (пустое пространство) теплопроводность равна нулю.
Каждый гомогенный (однородный) материал характеризуется коэффициентом теплопроводности (обозначается греческой буквой лямбда), то есть величиной, которая определяет, сколько тепла нужно передать через площадь 1 м², чтобы за одну секунду, пройдя через толщу материала в один метр, температура на его концах изменилась на 1 К. Это свойство присуще каждому материалу и изменяется в зависимости от его температуры, поэтому этот коэффициент измеряют, как правило, при комнатной температуре (300 К) для сравнения характеристики разных веществ.
Если материал является неоднородным, например, железобетон, тогда вводят понятие полезного коэффициента теплопроводности, который измеряется согласно коэффициентам однородных веществ, составляющих этот материал.
В таблице ниже приведены коэффициенты теплопроводности некоторых металлов и сплавов во Вт/(м*К) для температуры 300 К (27 °C):
- сталь 47—58;
- алюминий 237;
- медь 372,1—385,2;
- бронза 116—186;
- цинк 106—140;
- титан 21,9;
- олово 64,0;
- свинец 35,0;
- железо 80,2;
- латунь 81—116;
- золото 308,2;
- серебро 406,1—418,7.
В следующей таблице приведены данные для неметаллических твердых веществ:
- стекловолокно 0,03—0,07;
- стекло 0,6—1,0;
- асбест 0,04;
- дерево 0,13;
- парафин 0,21;
- кирпич 0,80;
- алмаз 2300.
Из рассматриваемых данных видно, что теплопроводность металлов намного превышает таковую для неметаллов. Исключение составляет алмаз, который обладает коэффициентом теплопередачи в пять раз больше, чем медь. Это свойство алмаза связано с сильными ковалентными связями между атомами углерода, которые образуют его кристаллическую решетку. Именно благодаря этому свойству человек чувствует холод при прикосновении к алмазу губами. Свойство алмаза хорошо переносить тепловую энергию используется в микроэлектронике для отвода тепла из микросхем. А также это свойство используется в специальных приборах, позволяющих отличить настоящий алмаз от подделки.
В некоторых индустриальных процессах стараются увеличить способность передачи тепла, чего достигают либо за счет хороших проводников, либо за счет увеличения площади контакта между составляющими конструкции.
Примерами таких конструкций являются теплообменники и рассеиватели тепла.
В других же случаях, наоборот, стараются уменьшить теплопроводность, чего достигают за счет использования теплоизоляторов, пустот в конструкциях и снижения площади контакта элементов.
Коэффициенты теплопередачи сталей
Способность передавать тепло для сталей зависит от двух главных факторов: состава и температуры.
Простые углеродные стали при увеличении содержания углерода снижают свой удельный вес, в соответствии с которым также уменьшается и их способность переносить тепло от 54 до 36 Вт/(м*К) при изменении процента углерода в стали от 0,5 до 1,5%.
Нержавеющие стали содержат в своем составе хром (10% и больше), которые вместе с углеродом образует сложные карбиды, препятствующие окислению материала, а также повышает электродный потенциал металла.
Теплопроводность нержавейки невелика в сравнении с другими сталями и колеблется от 15 до 30 Вт/(м*К) в зависимости от ее состава.
Жаропрочные хромоникелевые стали обладают еще более низкими значениями этого коэффициента (11—19 Вт/(м*К).
Другим классом являются оцинкованные стали с удельным весом 7 850 кг/м3, которые получают путем нанесения покрытий на сталь, состоящих из железа и цинка. Так как цинк легче проводит тепло, чем железо, то и теплопроводность оцинкованной стали будет относительно высокой в сравнении с другими классами стали. Она колеблется от 47 до 58 Вт/(м*К).
Теплопроводность стали при различных температурах, как правило, не изменяется сильно. Например, коэффициент теплопроводности стали 20 при увеличении температуры от комнатной до 1200 °C снижается от 86 до 30 Вт/(м*К), а для марки стали 08Х13 увеличение температуры от 100 до 900 °C не изменяет ее коэффициент теплопроводности (27—28 Вт/(м*К).
Факторы, влияющие на физическую величину
Способность проводить тепло зависит от ряда факторов, включая температуру, структуру и электрические свойства вещества.
Температура материала
Влияние температуры на способность проводить тепло различается для металлов и неметаллов. В металлах проводимость главным образом связана со свободными электронами. Согласно закону Видемана—Франца теплопроводность металла пропорциональна произведению абсолютной температуры, выраженной в Кельвинах, на его электропроводность. В чистых металлах с увеличением температуры уменьшается электропроводность, поэтому теплопроводность остается приблизительно постоянной величиной. В случае сплавов электропроводность мало изменяется с ростом температуры, поэтому теплопроводность сплавов растет пропорционально температуре.
С другой стороны, передача тепла в неметаллах главным образом связана с колебаниями решетки и обмене решеточными фононами.
За исключением кристаллов высокого качества и низких температур, путь пробега фононов в решетке значительно не уменьшается при высоких температурах, поэтому и теплопроводность остается постоянной величиной во всем температурном диапазоне, то есть является незначительной. При температурах ниже температуры Дебая способность неметаллов проводить тепло, наряду с их теплоемкостью, значительно уменьшается.
Фазовые переходы и структура
Когда материал испытывает фазовый переход первого рода, например, из твердого состояния в жидкое или из жидкого в газ, то его теплопроводность может измениться. Ярким примером такого изменения является разница этой физической величины для льда (2,18 Вт/(м*К) и воды (0,90 Вт/(м*К).
Изменения кристаллической структуры материалов также влияют на теплопроводность, что объясняется анизотропными свойствами различных аллотропных модификаций вещества одного и того же состава.
Анизотропия влияет на различную интенсивность рассеивания решеточных фононов, основных переносчиков тепла в неметаллах, и в различных направлениях в кристалле.
Здесь ярким примером является сапфир, проводимость которого изменяется от 32 до 35 Вт/(м*К) в зависимости от направления.
Электрическая проводимость
Теплопроводность в металлах изменяется вместе с электропроводностью согласно закону Видемана—Франца.
Это связано с тем, что валентные электроны, свободно перемещаясь по кристаллической решетке металла, переносят не только электрическую, но и тепловую энергию.
Для других материалов корреляция между этими типами проводимости не является ярко выраженной, ввиду незначительного вклада электронной составляющей в теплопроводность (в неметаллах основную роль в механизме передачи тепла играют решеточные фононы).
Процесс конвекции
Воздух и другие газы являются, как правило, хорошими теплоизоляторами при отсутствии процесса конвекции. На этом принципе основана работа многих теплоизолирующих материалов, содержащих большое количество небольших пустот и пор.
Такая структура не позволяет конвекции распространяться на большие расстояния. Примерами таких материалов, полученных человеком, являются полистирен и силицидный аэрогель.
В природе на том же принципе работают такие теплоизоляторы, как шкура животных и оперение птиц.
Легкие газы, например, водород и гель, имеют высокие значения теплопроводности, а тяжелые газы, например, аргон, ксенон и радон, являются плохими проводниками тепла.
Например, аргон, инертный газ, который тяжелее воздуха, часто используется в качестве теплоизолирующего газового наполнителя в двойных окнах и в электрических лампочках.
Исключением является гексафторид серы (элегаз), который является тяжелым газом и обладает относительно высокой теплопроводностью, ввиду его большой теплоемкости.
Теплоотдача 1 м стальной трубы – проводим расчет
Расчёт теплоотдачи трубы требуется при проектировании отопления, и нужен, чтобы понять, какой объём тепла потребуется, чтобы прогреть помещения и, сколько времени на это уйдёт. Если монтаж производится не по типовым проектам, то такой расчёт необходим.

Стальная труба
Для каких систем нужен расчёт?
Коэффициент теплоотдачи считается для тёплого пола. Всё реже эта система делается из стальных труб, но если в качестве теплоносителей выбраны изделия из этого материала, то произвести расчёт необходимо. Змеевик – ещё одна система, при монтаже которой необходимо учесть коэффициент отдачи тепла.

Радиатор из стальных труб
Регистры – представлены в виде толстых труб, соединённых перемычками. Теплоотдача 1 метра такой конструкции в среднем – 550 Вт. Диаметр же колеблется в пределах от 32 до 219 мм.
Сваривается конструкция так, чтобы не было взаимного подогрева элементов. Тогда теплоотдача увеличивается.
Если грамотно собрать регистры, то можно получить хороший прибор обогрева помещения – надёжный и долговечный.
Как оптимизировать теплоотдачу стальной трубы?
В процессе проектирования перед специалистами встаёт вопрос, как уменьшить или увеличить теплоотдачу 1 м. стальной трубы. Для увеличения требуется изменить инфракрасное излучение в большую сторону. Делается это посредством краски. Красный цвет повышает теплоотдачу. Лучше, если краска матовая.
Расчет
Другой подход – установить оребрение. Оно монтируется снаружи. Это позволит увеличить площадь теплоотдачи.
В каких же случаях требуется параметр уменьшить? Необходимость возникает при оптимизации участка трубопровода, расположенного вне жилой зоны. Тогда специалисты рекомендуют утеплить участок – изолировать его от внешней среды. Делается это посредством пенопласта, специальных оболочек, которые производятся из особого вспененного полиэтилена. Нередко используется и минеральная вата.
Производим расчёт
Формула, по которой считается теплоотдача следующая:
Q = K*F*dT, где
- К – коэффициент теплопроводности стали;
- Q – коэффициент теплоотдачи, Вт;
- F – площадь участка трубы, для которого производится расчёт, м2 dT – величина напора температуры (сумма первичной и конечной температур с учётом комнатной температуры), ° C.
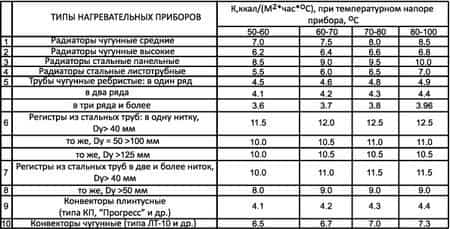
Коэффициент теплопроводности K выбирается с учётом площади изделия. Зависит его величина и от количества ниток, проложенных в помещениях. В среднем величина коэффициента лежит в пределах 8-12,5.

dT называется также температурным напором. Чтобы параметр высчитать, нужно сложить температуру, которая была на выходе из котла, с температурой, которая зафиксирована на входе в котёл. Полученное значение умножается на 0,5 (или делится на 2). Из этого значения вычитается комнатная температура.
dT = (0,5*(T1 + T2)) — Tк
Если стальная труба изолирована, то полученное значение умножается на КПД теплоизоляционного материала. Он отражает процент тепла, который был отдан при прохождении теплоносителя.

Рассчитываем отдачу для 1 м. изделия
Посчитать теплоотдачу 1 м. трубы, выполненной из стали, просто. У нас есть формула, осталось подставить значения.
Q = 0,047*10*60 = 28 Вт.
Здесь
- К = 0.047, коэффициент теплоотдачи;
- F = 10 м2, площадь трубы;
- dT = 60° С, температурный напор.
Об этом стоит помнить
Хотите сделать систему отопления грамотно? Не стоит подбирать трубы на глазок. Расчёты теплоотдачи помогут оптимизировать траты на строительство. При этом можно получить хорошую отопительную систему, которая прослужит долгие годы.
Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах
Теплоотдача при вынужденном течении жидкости в трубах и каналах
- Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).
- При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.
- Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).
- Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м2·град), который определяется по формуле:
- Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
- d – эквивалентный диаметр, равный
- F – площадь сечения канала, м2; П – периметр канала, м.
- Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.
- В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.
- Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.
- Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
- При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
- Турбулентный режим течения в трубах наблюдается при числах Re более 10000.
- Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).
- Число Re определяется по формуле:
- w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м2/с.
Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.
Теплоотдача при ламинарном течении в трубах и каналах
Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.
Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.
- g – ускорение свободного падения, м/с2;
- β – температурный коэффициент объемного расширения, град-1;
- d – эквивалентный диаметр канала, м;
- ν — кинематическая вязкость жидкости при средней температуре, м2/с;
- Δt – средняя разность температур жидкости и стенки, °С.
- Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·105, то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:
- Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.
- Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки.
- εL – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:
| εL | 1,9 | 1,7 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1 |
Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr50, то коэффициент εL=1.
- Выполним расчет числа Нуссельта по приведенному критериальному уравнению:
- 5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:
- Выполним расчет:
- Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м2·град).
Теплоотдача при свободной конвекции в трубах и каналах
Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.
Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).
Свободная конвекция в неограниченном пространстве
Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 103 до 109 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:
- В качестве определяющего размера принимается наружный диаметр d канала или трубы.
- Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 103 до 109 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:
- При GrPr>109:
Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.
Свободная конвекция в ограниченном объеме
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.
- Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λэк.
- Эквивалентный коэффициент теплопроводности определяется по формуле:
- Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м2; Δt=tc1-tc2 — температурный напор между нагретой и холодной стенками, °С.
- Отношение эквивалентного коэффициента теплопроводности λэк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции εк, который определяется значением комплекса GrPr.
- При малых значениях комплекса GrPr