- Расчет производительности холодильников
- Время охлаждения (нагрева)
- Расчет в Excel времени охлаждения (нагрева)
- Исходные данные:
- Алгоритм расчета:
- Проверка расчета опытом
- P.S
- P.P.S
- Примерная длительность охлаждения отливок
- 14 Теплопроводность при нестационарном режиме
- Аналитическое решение нестационарных задач теплопроводности
- Примечание. Общее время нагрева штанги tобщ с учетом времени выдержки составит 36 мин + 12 мин = 48 мин, а с учетом выбранной схемы укладки (например по схеме 3 таблица 9 приложения):
- tобщ = 36 × 2 + 12 = 84 мин = 1 ч 42 мин.
- 4 Расчет времени охлаждения
- 4.1 Расчет времени охлаждения в среде с постоянной температурой
Пример 4.
Определить продолжительность охлаждения центра вала из стали 40Х, диаметром 600 мм, длиной 3 м с температурой 850ºС до температуры 200ºС в различных охлаждающих средах (вода, масло, воздух).
- По таблице 3 приложения принимаем коэффициент теплоотдачи.
- aводы = 1163 Вт/м2 ºС;
- aмасло = 348,9 Вт/м2 ºС;
- aвоздух = 98,9 Вт/м2ºС.
- Средний коэффициент теплопроводности lср(от температуры нагрева до температуры охлаждения) будет равен » 37,75 Вт/м2 °С (по таблице 5 приложения). Зная l и R находим критерий Био по формуле (13):
- при охлаждении в воде:
при охлаждении в масле:
при охлаждении на воздухе:
Определяем температурный критерий q(для случая охлаждения):
Для случая охлаждения в воде или на воздухе:
Для случая охлаждения в масле:
- Тогда критерий Фурье, определенный по рисунку А.1, б (приложение):
- при охлаждении в воде Fo= 0,4 (Bi = 9,03; θ = 0,21);
- при охлаждении в масле Fo = 0,68 (Bi = 2,77; θ = 0,19); при охлаждении на воздухе Fo = 1,4 (Bi = 0,79; θ = 0,21).
- Коэффициент теплопроводности взят для аустенитного состояния при 800ºС, λ = 26,7 Вт/мºС (таблица 5, приложение), теплоемкость С = 687 Дж/кгºС (таблица 6, приложение) и γ = 7830 кг/м3.
- Определим коэффициент температуропроводности по формуле (21):
Критерий Фурье по формуле (20):
- Тогда:
- Подставляя значения Foдля различных сред охлаждения, находим: при охлаждении в воде:
при охлаждении в масле:
- при охлаждения на воздухе:
- 4.2 Расчет времени охлаждения в среде о переменной
- температурой
4.2.1 Расчет времени охлаждения в масле
Пример 5. Определить время охлаждения центра вала диаметром 200 мм, длиной 3 м, весом 700 кг с температурой 800ºС до 200ºС в баке о маслом объемом 4 м3 при начальной температуре масла 30ºС.
- «Водяное число» масла при удельном весе γж = 0,9 кг/л с теплоемкостью Сж = 2,06 кДж/кгºС определим по формуле:
- где Vж – объем жидкости (масла);
- γж – удельный вес жидкости (масла);
- Сж – теплоемкость жидкости (масла).
- «Водяное число» вала весом Gм = 700 кг и с теплоемкостью См = 0,687 кДж/кгºС (таблица 6, приложение) определим по формуле:
- Отношение «водяных чисел»:
- Подставляя значения, «водяных чисел» в уравнение (23) получим:
Следовательно, температура масла повысится с 30º до 78ºС, т.е. на 48ºС, а температура охлаждаемого металла снизится с 800º до 800 – 78 = 722ºС.
Принимая a =581,5 Вт/м2ºС (см. пункт 1.4), l =34,9 Вт/м2ºС (таблица 5, приложение).
- Подставляя наеденные значения (для встречного потока) в уравнение (26) получим:
- откуда:
- Значение температурного коэффициента θ находим по формуле (19):
- По значениям Biусл=1,61 и θ=0,17 по рисунку А.1, б (приложение) находим Fo=0,8, что соответствует расчетным данным по формуле (20), которая была преобразована в формулу (22), определяем время охлаждения:
- Поскольку охлаждение ведется в баке с маслом, без принудительного охлаждения его происходит постепенное повышение его температуры за счет вносимого металлом тепла. Для того, чтобы при закалке не происходило резкого повышения температуры масла, рекомендуется принимать отношение веса жидкости к весу закаливаемого металла равным:
- В нашем примере
4.2.2 Расчет времени охлаждения изделий при душевой закалке
- Пример 6: Определить время охлаждения сложных профилей при душевой закалке: швеллера №20 (200×55×3,2 мм), уголка №9 (90×90×6 мм), балки №20 (200×65×3,2 мм) с температуры конца прокатки (1000ºС) до температуры начала самоотпуска 450ºС при закалке изделий обрызгиванием (душевая закалка) для малоуглеродистой и низколегированной сталей.
- Определим вес изделий:
- для швеллера №20:
- для балки №20:
- для уголка №9:
- По таблице 6 приложения определяем, с=0,682 кДж/кгºС.
- По таблице 3 приложения определяем λ450:
- Определим поверхности закаливаемых изделий:
- для швеллера №20:
- для балки №20:
- для уголка №9:
- Определим время охлаждения до температуры 450ºС по формуле:
- для швеллера №20:
Расчет производительности холодильников
| Заказать ✍️ написание работы |
Для расчета времени нагрева и охлаждения металла используют три группы формул [6]. Одни из них основаны на радиационном законе Стефана – Больцмана и рекомендуются для расчета в области высоких температур, вторые исходят из конвективного закона Ньютона и применяются, когда температуры металла сравнительно низки, третьи являются чисто эмпирическими.
После интегрирования соответствующих дифференциальных законов теплообмена получают следующие уравнения для длительности процессов изменения температуры от Т1 до Т2 °С:
где tохл – время процесса, с; G – масса металла, т; с – средняя его теплоемкость в рассматриваемом диапазоне температур, МДж/(т×К); Sоб – поверхность, через которую осуществляется теплообмен, м2; e – степень черноты металла; С0 » 6×10-8 Вт/(м2×К4) – постоянная лучеиспускания абсолютно черного тела; a – коэффициент теплоотдачи, Вт/(м2×К); Т0 – температура среды, 0С.
Эти уравнения записаны для охлаждения, когда Т1 > Т2; при расчетах нагрева следует поменять индексы.
Хотя обе формулы исходят из теоретических законов, при получении их принято грубое допущение о независимости от температуры удельной теплоемкости металла с, а также параметров e и a.
В то же время в диапазоне 720 – 900 °С удельная теплоемкость низкоуглеродистой стали немонотонно изменяется от 1,88 до 0,75 МДж/(т×К), т. е. в 2,5 раза, а коэффициент теплоотдачи на воздухе – от 63 до 100 Вт/(м2×К), т. е. в 1,8 раза. Удельную теплоемкость заменяют средней
где i – теплосодержание металла, МДж/т (записано для охлаждения); коэффициент теплоотдачи или степень черноты также приобретают смысл некоторых поправочных коэффициентов, согласующих теорию с экспериментом. В них часто учитывается при использовании конкретной формулы действие альтернативных механизмов теплообмена, поскольку лучистый конвективный теплообмен и теплопроводность всегда сосуществуют.
Производительность холодильников [1] (рис. 2) определяется конструкцией и размерами его, количеством охлаждаемого металла и временем его охлаждения до заданной температуры.
- Рисунок 2. Реечный односторонний холодильник мелкосортного стана 250 (поперечные разрезы):
- 1 – подводящий рольганг; 2 – отводящий рольганг; 3 – неподвижные рейки; 4 – продольные балки; 6 – эксцентрики; 7 – электродвигатели; 8, 10 – редукторы; 9 – наклонные клапаны; 11 – тележка; 12 – привод тележки; 13 – кривошипно-рычажная передача; 14 – опорные балки
- Последовательность расчета производительности холодильников такова. Определяют количество тепла, содержащегося в прокатанных полосах при поступлении их на стеллажи холодильника на 1 м длины:
где с – теплоемкость стали, кДж/(кг×°С); T1 – температура, с которой прокатанная полоса поступает на холодильник, °С; G' – масса 1 м длины полосы, кг.
В охлажденной до заданной температуры полосе будет содержаться количество тепла, определяемого по формуле
где Т2 – температура конца охлаждения полосы, °С.
Определяют среднюю температуру охлаждаемых полос на холодильнике по формуле
а количество тепла, кДж, отданное полосой в процессе охлаждения, по формуле
- Время, необходимое для охлаждения полосы на холодильнике, составляет
- , (40)
- где a – коэффициент теплоотдачи между полосой и окружающей средой, Вт/(м2×°С); Fох – площадь охлаждаемой поверхности 1 м длины полосы, м2.
- Согласно [6] следствием конвективной формулы (34) является зависимость, рекомендуемая для подсчета времени охлаждения металла на холодильниках без принудительного воздушного душирования:
- , (41)
- где tохл – время охлаждения, мин;
- F и П – площадь, см2, и периметр сечения, см.
- Для круглой и квадратной стали, имеющей диаметр или сторону сечения d: F/П=d/4; для листовой толщиной h: F/П » h/2.
Для тех же условий полезно также следующее практическое наблюдение: время охлаждения круглой стали в диапазоне 1000 – 150 °С в минутах примерно равно ее диаметру в миллиметрах.
Сталь круглая диаметром 10 мм стынет за 10 мин, а 60 мм – за 1 ч. Все другие профили, имеющие относительно большую поверхность, охлаждаются быстрее.
Для них верхнюю оценку времени охлаждения можно делать по формуле, обобщающей приведенное выше наблюдение:
t £ 40F/П. (42)
Размерности всех величин здесь такие же, как и в уравнении (41). Для учета воздушного душирования можно использовать известные данные Г. П. Иванцова, согласно которым время охлаждения уменьшается для проката толщиной 20 мм в 1,7 – 1,8, а толщиной 100 мм – в 1,35 – 1,4 раза при увеличении скорости потока воздуха относительно охлаждаемого металла от нуля до 2 м/с.
- По данным [3] время охлаждения проката устанавливают на основании практических данных. Можно определить время охлаждения по следующим эмпирическим формулам:
- для охлаждения нерулонной полосовой стали:
- мин, (43)
- где b – ширина полосы, м;
- T1 – температура полосы после выхода из стана, °С;
- T2 – то же, после охлаждения на холодильнике, °С;
- для охлаждения мелкосортной стали:
- ч, (44)
- где qП – масса 1 пог. м профиля, кг;
- F – поверхность охлаждения, м2;
- T'1 – абсолютная температура проката после выхода из стана;
- Т'2 – то же, после охлаждения на холодильнике.
При использовании эмпирических формул следует учесть, что они даны для расчета времени охлаждения металла на воздухе. В действительности прокат охлаждается в потоке воздуха, а в начале холодильника — на водоохлаждаемых столах. Поэтому время охлаждения фактически будет меньше, чем по этим формулам [3].
- Число полос, шт/ч, поступающих со стана на холодильник, определяют по формуле
- , (45)
- где А – производительность стана, т/ч.
- Далее устанавливают предварительные размеры холодильника:
- его длину (46)
- и ширину , (47)
- где а – расстояние между соседними полосами, лежащими на стеллажах холодильника, м; f – коэффициент укладки полос на стеллажах холодильника, равный 0,9 – 1,1.
- Одновременно на стеллажах шлепперного холодильника размещается число полос, равное
- , (48)
- где В1 – ширина стеллажей холодильника, приходящаяся на одну охлаждаемую полосу (ширина проката), м.
- Для реечного холодильника число профилей, вмещающихся на холодильнике [3]
- , (49)
- где s – шаг зубчатой рейки, мм.
- Тогда время, мин, пребывания полосы на стеллажах холодильника до поступления следующей полосы будет равно
- , (50)
- а загрузка холодильника составит
- . (51)
- Часовая производительность одной секции шлепперного холодильника [3]
- , (52)
- где G – масса охлаждаемого проката, т;
- tохл – время охлаждения проката, ч.
- Подставляя значение n' для шлепперных холодильников, получаем часовую производительность одной его секции
- , (53)
- а для реечных холодильников (n'')
- . (54)
Воспользуйтесь поиском по сайту:
Время охлаждения (нагрева)
Опубликовано 14 Июл 2018Рубрика: Теплотехника | 65 комментариев
…характеризуется скоростью теплового обмена, которая пропорциональна разности температур тела и окружающего пространства.
В отличие от стационарного режима, при котором температуры всех точек системы остаются неизменными длительное время, нестационарный теплообмен возникает, например, при помещении тела в среду с более низкой или более высокой температурой.
Если среда – это условно бесконечное пространство (например, атмосферный воздух или вода в «большой» ёмкости), то влияние тела на температуру среды ничтожно, поэтому охлаждение (нагрев) тела происходит при условно постоянной температуре окружающего газа или жидкости.
Заметим, что охлаждение тела сточки зрения математики – это нагрев со знаком «минус». И нагрев, и охлаждение описываются одними и теми же формулами!
О каких задачах может идти речь? Представим небольшой перечень вопросов, на которые можно попытаться ответить, используя предложенный далее расчет в Excel:
- Сколько времени будет нагреваться деталь в печи?
- Сколько времени остывает отливка после выбивки из формы?
- Сколько времени требуется для нагрева воды в бочке на даче?
- Через какое время перемерзнет наружный водопровод при отсутствии разбора?
- Сколько времени нужно на охлаждение банки пива в холодильнике?
Расчет в Excel времени охлаждения (нагрева)
Алгоритм расчета базируется на законе Ньютона-Рихмана и на теоретических и практических исследованиях регулярного теплового режима советскими учеными Г.М. Кондратьевым («Регулярный тепловой режим», Москва, 1954г.) и М.А. Михеевым («Основы теплопередачи», Москва, 1977 г.).
Для примера выбран расчет времени нагрева до +22 °C в комнате с температурой воздуха +24 °C пивной алюминиевой банки с водой, предварительно охлажденной до +13 °C.
Исходные данные:
Параметров, необходимых для выполнения расчета времени охлаждения (нагрева) – 12 (см. скриншот).
Ориентировочные сведения о значениях коэффициента теплоотдачи α приведены в примечании к ячейке D3.
Теплофизические характеристики материала тела λ, a, ρ, c легко можно найти в справочниках или по запросу в Интернете. В нашем примере – это параметры воды.
В принципе, для выполнения расчета достаточно знать значения любой из пар характеристик: λ, a или ρ, c. Но для возможности выполнения проверки и минимизации вероятности ошибки рекомендую заполнить значениями все 4 ячейки.
Вводим значения исходных данных в соответствующие ячейки листа Excel и считываем результат: нагрев воды от +13 °C до +22 °C в спокойном воздухе комнаты с постоянной температурой +24 °C будет длиться 3 часа 25 минут.
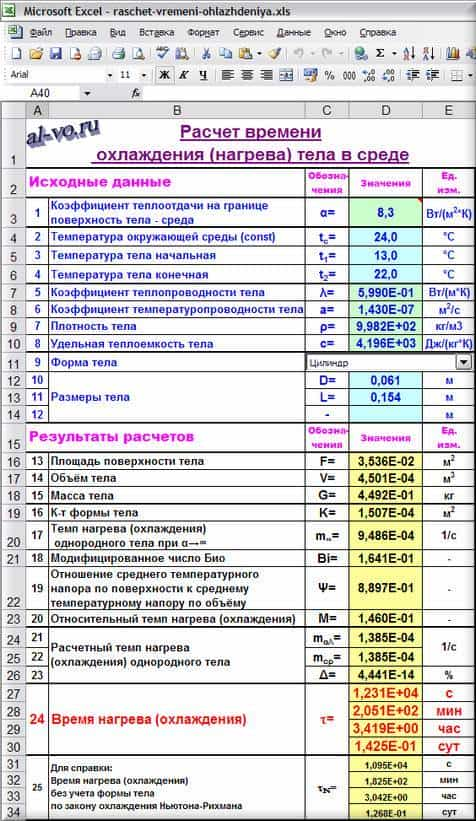
Для справки в самом конце таблицы вычислено время нагрева без учета формы тела – 3 часа 3 минуты.
Алгоритм расчета:
- 13.1. F=2·H·L+2·B·L+2·H·B – для параллелепипеда;
- 13.2. F=π·D·L+2·π·D2/4 – для цилиндра;
- 13.3. F=π·D2 – для шара.
- 14.1. V=H·L·B – для параллелепипеда;
- 14.2. V=L·π·D2/4 – для цилиндра;
- 14.3. V=π·D3/6 – для шара.
- 15. G=ρ·V
- 16.1 K=((π/H)2+(π/L)2+(π/B)2)-1 – для параллелепипеда;
- 16.2 K=((2,405/(D/2))2+(π/L)2)-1 – для цилиндра;
- 16.3 K=((D/2)/π)2 – для шара.
- 17. m∞=a/K
- 18. Bi=α·K·F/(λ·V)
- 19. Ψ=(1+1,44·Bi+Bi2)-0,5
- 20. M=Ψ·Bi
- 21. mαλ=M·m∞
- 22. mcρ=Ψ·α·F/(c·ρ·V)
- 23. Δ=ABS (1-mαλ/mcρ)·100
- 24. t=(LN (ABS (tc-t1)) -LN (ABS (tc-t2))/mαλ
- 25. tN=(LN (ABS (tc-t1)) -LN (ABS (tc-t2)))·c·ρ·V/(α·F)
Проверка расчета опытом
Как не трудно догадаться такой несколько странный пример выбран не случайно, а для возможности проведения простого опыта и последующего сравнения результатов. Были взяты термометр, часы и произведены замеры температуры воды в банке в процессе нагревания. Результаты расчетов и опыта отражены на графиках.
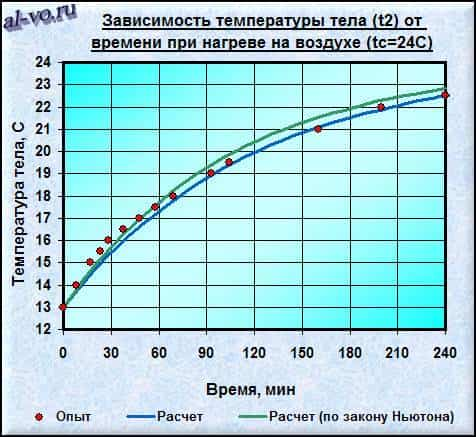
Результаты проведенного опыта показали, что нагрев банки с водой от +13 °C до +22 °C в комнате (+24 °C) продолжался примерно 3 часа 20 минут. Это на 5 минут меньше расчетного времени по Кондратьеву и на 17 минут дольше времени по классическому закону Ньютона-Рихмана.
Близость результатов и радует, и удивляет.
Но не стоит переоценивать полученные итоги! Время охлаждения (нагрева), вычисленное по предложенной программе расчета в Excel, можно использовать лишь для приблизительных оценок продолжительности процессов! Дело в том, что принятые в расчете константами теплофизические характеристики тела и коэффициент теплоотдачи таковыми на самом деле не являются. Они зависят от изменяющейся температуры! К тому же регулярный режим теплообмена устанавливается не сразу после помещения тела в среду, а спустя какое-то время.
Обратите внимание, что полученные из опыта значения температур банки с водой в течение первого часа расположены выше теоретической расчетной кривой (см. графики). Это означает, что коэффициент теплоотдачи в этом периоде времени был больше выбранного нами значения α=8,3 Вт/(м2·К).
Определим среднее значение α в первые 58 минут из результатов опыта. Для этого:
- Запишем t2=17,5 °C в ячейку D6.
- Активируем («встанем мышью») ячейку D28.
- Выполним: Сервис – Подбор параметра.
- И установим в D28 значение 58 минут, изменяя ячейку D3.
α=9,2 Вт/(м2·К)!!!
Проделав ту же процедуру для t2=22,5 °C и t=240 мин, получим α=8,3 Вт/(м2·К).
Выбранное при теоретическом расчете значение α (по рекомендации СП 50.13330.2012 и формуле из Справочника по физике – см. примечание к ячейке D3) чудесным образом, хотя и совершенно случайно, совпало со значением α, вычисленным по опытным данным.
- Рассмотренным способом можно определять реальные точные средние значения коэффициента теплоотдачи тел с любой формой поверхности по практическим замерам всего двух значений температуры тела и промежутка времени между этими замерами.
- Остается добавить, что температура банки с водой после рассмотренных 4-х часов в последующее время будет асимптотически приближаться к 24 °C.
- Прошу уважающих труд автора скачивать файл с программой расчетов после подписки на анонсы статей!
- Ссылка на скачивание файла: vremya-ohlazhdeniya (xls 55,5KB).
P.S
Так сколько часов составит время охлаждения алюминиевой банки с пивом 0,45 л от +20 °C до +8 °C в холодильнике (+3°C)? По расчету в программе – 2,2…2,4 часа. Опытом не проверял… ?
P.P.S
Любопытный (возможно, только для меня) факт обнаружился при работе над статьей. И у куба с размером ребер a, и у цилиндра с диаметром а и длиной а, и у шара с диаметром а отношение объема к площади поверхности одинаковое: V/F=a/6!!!
Другие статьи автора блога
На главную
Примерная длительность охлаждения отливок
Литье
Литье является одним из экономичных способов получения деталей и заготовок сложной формы, больших и малых размеров из различных металлов, сплавов, пластмасс и других материалов. Этот способ заключается в заливке расплавов в специально приготовленные литейные формы.
В литейном производстве для получения металлических отливок применяют более 50 разновидностей литья: литье в песчаные формы, в оболочковые формы, по выплавляемым моделям, литье в кокиль, центробежное литье, литье под давлением и др.
Литейная форма— это применяемая в литейном производстве форма для получения отливок, состоит из собственно формы для воспроизведения наружных контуров отливок и литейных стержней для образования внутренних полостей и отверстий (рис. 3.1).
Рабочая часть литейной формы представляет собой полость, в которой материал, охлаждаясь, затвердевает и принимает требуемые конфигурацию и размеры.
Литейный стержень — это отъемная часть литейной формы, оформляющая внутренние полости отливки. В тех случаях, когда конфигурация литейной модели затрудняет извлечение ее из литейной формы, литейные стержни могут использоваться и для формирования наружных частей отливки. Литейные стержни устанавливают на специальные опорные поверхности литейной формы, называемые знаками.
Литье в песчаные формы— это способ получения отливок в литейных формах, изготовленных из песчано-глинистых формовочных материалов и используемых для получения одной отливки.
Совокупность каналов (элементов), служащих для заполнения рабочей полости литейной формы расплавленным металлом, питания отливки при затвердевании и улавливания первых порций металла, шлака и загрязнений, называется литниковой системой. Основными элементами литниковой системы являются чаша, стояк, шлакоуловитель, питатель, боковая прибыль, шейка.
Выпар — это вертикальный канал, соединенный с литниковой системой. Он расположен в верхней части литейной формы и предназначен для выхода газов при заполнении формы жидким металлом, контроля заполнения формы, а иногда — питания отливки металлом во время ее остывания.
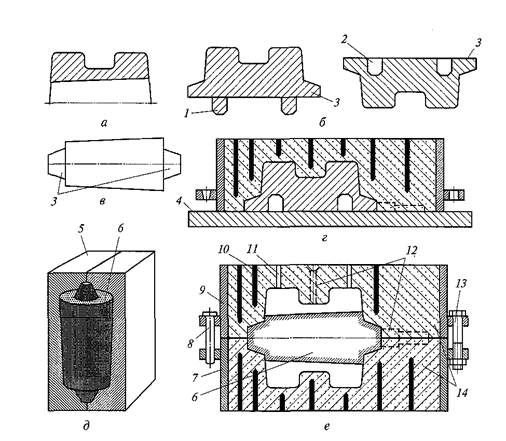
Рис. 3.1.
Последовательность изготовления формы (формовка): а — эскиз детали; б — эскиз полу-модели; в — стержень; г — изготовление нижней полу-формы; д — изготовление стержня; е — форма в сборе; 1 — базовый выступ; 2 — базовая впадина; 3 — знак; 4 — модельная плита; 5 — стержневой ящик; 6 — стержень; 7 — нижняя опока; 8 — зажимной болт; 9 — верхняя опока; 10 — вентиляционный канал; 11 — выпар; 12 — литниковая система; 13 — базовый штифт; 14 –полу-формы.
Разовые литейные формы получают с помощью специальных комплектов приспособлений — модельного и формовочного.
Модельный комплект необходим для образования при формовке рабочей полости литейной формы. В комплект входят литейная модель, стержневые ящики, модели литниковой системы, шаблоны для конкретной отливки, модельные плиты и др.
Литейная модель — это часть модельного комплекта, служащая для образования в литейной форме отпечатка, соответствующего конфигурации и размерам отливки. Модели изготавливают из древесины, металлических и специальных модельных сплавов и пластмасс.
Существуют одноразовые модели и модели для многократного использования. Деревянные модели отличаются простотой изготовления, невысокой стоимостью, относительно малой массой, однако они недолговечны.
Применение деревянных моделей целесообразно в опытном и разовом производстве.
Модельная плита — это плита, оформляющая разъем литейной формы и несущая на себе различные части модели, включая литниковую систему, и служащая для набивки формовочной смесью одной из парных опок.
Стержневой ящик — приспособление, служащее для изготовления стержней. Конструкция стержневого ящика зависит от формы и размеров стержня, способа его изготовления. Для свободного , удаления стержня из ящика на соответствующих поверхностях предусматривают формовочные уклоны. Стержневые ящики могут быть изготовлены из дерева, металла или пластмассы.
В формовочный комплект входят опоки, штыри, скобы и другие приспособления, необходимые для получения разовой песчаной формы.
Опокой называют приспособление в виде жесткой рамы (открытого ящика), служащее для удержания в нем формовочной смеси при изготовлении разовых песчаных форм, транспортирования и заливки металла. Опоки изготавливают из стали, чугуна, алюминиевых сплавов.
Основными операциями при изготовлении литейной формы являются: уплотнение формовочной смеси, придание форме достаточной прочности и устройство вентиляционных каналов.
Изготовление литейной формы начинают с того, что на модельную плиту 4 (см. рис. 3.1) устанавливают нижнюю половину модели и нижнюю опоку 7 рабочей плоскостью вниз. На модель наносят слой облицовочной смеси толщиной 40… 100 мм, который слегка уплотняют. Затем опоку заполняют наполнительной смесью и уплотняют.
Опоку с заформованной в ней половиной модели поворачивают на 180° и вновь устанавливают на модельную плиту. На нижней половине модели фиксируют ее верхнюю половину, устанавливают модели стояка и выпаров. На нижнюю опоку устанавливают верхнюю, извлекают модели стояка и выпара.
Верхнюю полу-форму снимают, поворачивают на 180° извлекают половины моделей отливки и литниковой системы.
Затем в нижнюю полу-форму устанавливают литейный стержень, который оформляет внутреннюю полость отливки, и на нижнюю полу-форму с помощью штырей устанавливают верхнюю полу-форму.
Для улучшения газопроницаемости формы делают вентиляционные каналы 10. После скрепления опок литейная форма считается подготовленной к заливке.
Изготовление отливок в песчаных формах включает в себя следующие основные технологические операции: заливку литейной формы расплавленным металлом, охлаждение отливки в литейной форме, выбивку отливки из литейной формы, обрубку и очистку отливок.
Заливка литейной формы заключается в равномерном заполнении литейной формы расплавленным металлом. Важное значение при заливке имеет обеспечение рациональной температуры заливки расплавленного металла, которая должна быть примерно на 100… 150° С выше температуры отвердения. Для крупных отливок из серого чугуна температура заливки обычно находится в пределах 1230…
1300° С, для мелких и средних отливок из серого чугуна — 1320… I400° С, для тонкостенных отливок — 1360… 1450° С. Высокопрочный и белый чугун заливают при температуре 1320… 1450º С, углеродистую и низколегированную стали — при температуре 1520… 1560° С. Для тонкостенных отливок из легированной коррозионностойкой стали 12Х18Н9ТЛ температура заливки достигает 1620° С.
Бронзу и латунь обычно заливают при температуре 1000…1 100° С, алюминиевые и магниевые сплавы — при 680… 760° С, титановые сплавы — при 1800… 1860° С.
Продолжительность заливки расплава в форму зависит от степени сложности конфигурации отливок, литейного сплава и металлоемкости литейной формы (рис. 3.2).
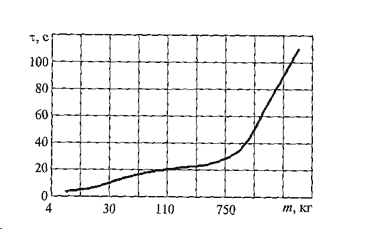
Рис. 3.2. Влияние массы отливки m на продолжительность заливки τ
Охлаждение отливок в литейных формах после заливки происходит от температуры заливки до достижения рациональной температуры выбивки. Продолжительность выдержки в форме определяется толщиной стенки отливки, свойствами залитого сплава и литейной формы, температурой выбивки и может быть рассчитана или определена экспериментально.
Небольшие тонкостенные отливки охлаждаются в форме в течение нескольких минут, а толстостенные крупные (массой 50…60 т) — в течение нескольких суток и даже недель (табл. 3.2).
| Характеристика отливок | Длительность охлаждения, час | ||
| Масса отливок, кг | Средняя толщина стенок, мм | Стальные отливки | Чугунные отливки |
| До 10 | 5… 15 | 0,2…0,5 | 0,2…0,4 |
| 10 …50 | 15…20 | 0,5…0,8 | 0,4… 0,6 |
| 50… 100 | 15 …30 | 2…5 | 0,8…2,0 |
| 100 …500 | 20… 50 | 6…8 | 4…6 |
| 500… 2 000 | 30… 80 | 18… 24 |
14 Теплопроводность при нестационарном режиме
где 5 — половина толщины тела (пластины) или радиус (шара и цилиндра); для тел сложной формы, X — половина наибольшего линейного размера.
При выполнении условия (14.1) тело называют термически тонким. В каждый момент времени температура t внутри такого тела успевает выровняться за счет интенсивного переноса теплоты теплопроводностью. Таким образом, значение t зависит только от времени т и не зависит от координат.
Рассмотрим термически тонкое тело произвольной формы с объемом К все точки которого охлаждаются за счёт теплоотдачи с одинаковой скоростью dt/dx. За время с/г тело отдает количество теплоты:
Одновременно эта теплота передается путем теплоотдачи к жидкости или газу с температурой (ж от поверхности F, имеющей температуру t тела:
По закону сохранения энергии
Введя избыточную температуру в = t — 1Ж, разделив переменные
и проинтегрировав выражение (14.5). получим:
Согласно начальным условиям (при г = 0. в — t 0 — t ж = в о) постоянная интегрирования С = In в0 7 следовательно,
Или
Таким образом, избыточная температура термически тонкого тела с течением времени уменьшается экспоненциально от начальной температуры &0 при г = 0 до нуля при г —? ос, и тем быстрее, чем больше комплекс aF/(c р V).
Формула (14.7) пригодна и при расчетах нагревания тела. В этом случае удобнее избыточную температуру считать по формуле в = — t и
соответственно &о = — to.
Аналитическое решение нестационарных задач теплопроводности
Если условие (14.1) не выполняется, то температура внутри охлаждаемого (или нагреваемого) тела зависит не только от времени, но и от координат, т.е.
разные участки тела охлаждаются с различной скоростью. Зависимость t — f (х, у, z, т) в этом случае можно получить, интегрируя нестационарное дифференциальное уравнение теплопроводности.
Это уравнение можно получить, рассмотрев баланс энергии произвольного объема V внутри тела. Выбранный объем ограничен замкнутой поверхностью F.
При отсутствии источников и стоков теплоты в объеме тела полный тепловой поток, уходящий через поверхность F согласно (8.2),
равен скорости изменения энтальпии (теплосодержания) вещества, заключенного в объеме
По теореме Остроградского — Гаусса:
Учитывая, что:
а
сравнивая выражения (14.9) и (14.10), получаем:
Равенство (14.11) справедливо для любого произвольно выбранного объема, поэтому подынтегральные выражения также равны друг другу. Тогда:
где а = Х/(с р) — коэффициент температуропроводности.
Это и есть нестационарное дифференциальное уравнение теплопроводности. Для его интегрирования необходимо задать начальные условия, определяющие температурное поле в рассматриваемом теле в начальный момент времени г = 0, и граничные условия, определяющие температуру или законы переноса теплоты на границе тела.
- В теплопередаче принята классификация граничных условий:
- I рода — задана температура на поверхности тела;
- II рода — задана плотность теплового потока на поверхности тела;
- III рода — поверхность тела обменивается теплотой со средой известной температуры по закону Ньютона (9.1);
- IV рода — рассматриваемое тело находится в плотном контакте с другим телом.
При решении стационарных задач теплопроводности граничные условия I рода были нами использованы в 8.3, а III рода — в 12.2.
Аналитические решения многих нестационарных задач для разнообразных условии можно найти в специальной литературе.
Здесь мы рассмотрим лишь одно из них — охлаждение бесконечной пластины в среде с постоянной температурой и при постоянном коэффициенте теплоотдачи (рисунок 14.1). (Распределение температуры по сечению пластины конечных размеров будет практически таким же, как в бесконечной, если рассматриваемое сечение отстоит от края на расстоянии, более чем в 10 раз превышающем толщину пластины.)
Рисунок 14.1 — К постановке задачи об охлаждении пластин
В этом одномерном случае (температура изменяется только по толщине пластины) уравнение (14.12) имеет вид:
с начальным условием:
Граничное условие III рода получается из баланса двух тепловых потоков: подходящего за счёт теплопроводности к поверхности остывающего тела из его глубины qx=s=—X(dt/dx)x=s и отводимого теплоотдачей к теплоносителю q = a (tc- (ж):
По условиям симметричности температурного поля при х = О
Аналитическое решение задачи (14.13) — (14.16) обычно приводится в безразмерном виде:
- где в = (t — to,c)/(to — to,c) — безразмерная температура;
- lin — корни характеристического уравнения ctg jnn = цп/Bi;
- Fo = az/S2 — число Фурье (безразмерное время);
- Bi = ад /X — число Био.
Число Био характеризует отношение термического сопротивления переносу теплоты теплопроводностью от середины твердого тела к поверхности Rx = S /(к F) к термическому сопротивлению теплоотдачи Ra-l /(aF). Условие (14.1) для термически тонкого тела можно записать в виде Bi —> 0 (практические! < 0,1).
Расчет по формуле (14.17) можно выполнить с помощью любого микрокалькулятора с простейшим программированием.
Вначале в интервале от 0 до тс/2 находят первый корень /о уравнения ctg цп = цп /Bi и рассчитывают первый член ряда, затем к нему суммируются последующие, для которых интервал цп сдвигается на значение тг по сравнению с предыдущим значением fi(„_j) (рисунок 14.2). Ряд быстро сходится, обычно достаточно шести членов. При Fo > 0,3 можно ограничиться одним первым членом.
Рисунок 14.2 — Графическое решение уравнения ctg /un=iin/Bi
Еще проще воспользоваться имеющимися в справочниках [9] номограммами, особенно если рассматриваемое тело цилиндрической или сферической формы, поскольку в решения таких задач входят специальные функции, а стандартных программ для их расчета у микроЭВМ нет.
Методы решения задач подобного рода рассматриваются в специальной науке — математической физике и в данном кратком курсе не приводятся. Правильность решения можно проверить его подстановкой в исходное уравнение, а также в начальные и граничные условия.
Распределение температуры по толщине пластины в различные моменты времени представляет собой семейство кривых в координатах 0, X (или t, х) с максимумом на оси пластины (рисунок 14.3).
Рисунок 14.3 — Распределение температуры по толщине охлаждаемой пластины
В любой момент времени Fq >0 (т > 0) касательные к кривой распределения температуры на границе пластины выходят из одной точки С, расположенной на оси X на расстоянии 1/Bi от поверхности пластины. Это несложно показать, если граничное условие (14.15) привести к безразмерному виду:
По определению производной (дв /дХ)х=1 = — tg (р (рисунок 14.3), следовательно, tg(p = Bi вс. Из рисунка 14.3 видно, что tg (р = АВ/АС, где АВ = 6С. Следовательно, АС= 1/Bi.
При больших значениях Bi (практически при Bi > 100), когда а » X /д , расстояние 1/Bi —? 0.
Это значит, что сразу после начала процесса поверхность тела охлаждается до температуры жидкости (рисунок 14.4, а). При таких режимах изменение температуры внутри тела определяется только термическим сопротивлением теплопроводности и дальнейшее увеличение а уже не ускоряет процесса охлаждения.
Случай малых значений Bi —> 0 специально рассмотрен в начале данной главы. При этом АС = (1/В1) —? со , т. е. температура по толщине пластины не изменяется (рисунок 14.4, б).
Решение (14.17) можно использовать и для расчетов температурного поля в бесконечном стержне прямоугольной формы и даже в параллелепипеде.
Такие тела рассматриваются как образованные пересечением двух или трех взаимно перпендикулярных бесконечных пластин, и безразмерная температура в любой их точке находится в виде произведения безразмерных температур в бесконечных пластинах, пересечением которых образовано данное тело
- Рисунок 14.4 — Распределение температуры по толщине охлаждаемой
- пластины
- Пример 14.1
- Рассчитать время нагрева круглого прутка из стали 20 диаметром 50 мм и длиной 2 м от 0 до 800 °С в электропечи с температурой 900 °С.
В пределах заданного интервала температуры нагрева детали теплофизические свойства металла и условия теплообмена сильно меняются, поэтому при выполнении точного расчета целесообразно этот интервал разбить на более мелкие и полное время нагрева найти в виде суммы.
В качестве иллюстрации метода выполним лишь приближенную оценку сразу для всего температурного интервала (методика расчета не зависит от величины интервала температур нагрева).
Теплофизические свойства металла и условия теплообмена будем считать при средней в заданном интервале нагрева температуре tM = 400 °С.
- В справочнике [15] найдем теплофизические свойства стали при =400 °С:
- Лм = 42,7 Вт/(м*К); рм = 7682 кг/м3; с = 682 Дж/(кг*К); е = 0,8.
- Теплофизические свойства воздуха при = 900 °С и tc = 400 °С:
- 1Ж = 7,63-Ю'2 Вт/(м К); уж = 155,1-10^ м2/с; Ргж = 0,717; Ргс = 0,678;
- рж = 1/Тж = 1/(273 + 900) = 8,5-1 O'4 1/К.
- Коэффициент теплоотдачи при естественной конвекции по аналогии с примером (10.2):
где
Коэффициент теплоотдачи излучением:
Суммарный коэффициент теплоотдачи будет равен:
Следует обратить внимание, что при высоких температурах теплообмен излучением является преобладающим и без большой погрешности величиной ак можно было бы пренебречь и не рассчитывать её.
Для выбора способа расчёта времени нагрева вычислим:
Здесь также следует обратить внимание на то, что в число Bi входит теплопроводность нагреваемого тела (металла), а в число Миж — теплопроводность газа.
Поскольку Bi F/V=4/d (площадью торцов пренебрегаем), получим: