- Электронная проводимость металлов
- Учебное особие по физике
- Конспект урока физики "Электронная проводимость металлов. Зависимость сопротивления проводника от температуры. Сверхпроводимость
- Электрический ток в металлах: подробное объяснение (формулы)
- Важно знать
- Классическая модель проводимости
- Выводы простым языком
- Классическая электронная теория проводимости Друде-Лоренца
- Формула Друде
- Опыт Толмена и Стюарта
Как вы знаете, электрический ток могут проводить и твердые, и жидкие, и газообразные тела. На практике, чаще всего применяются металлические проводники. Можно привести много примеров: линии электропередач, обеспечивающие передачу энергии от различных источников тока к потребителям.
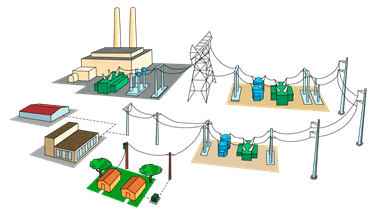
Генераторы, электронагревательные приборы и так далее. Как мы уже говорили ранее, хорошими проводниками являются некоторые растворы. Наиболее распространенный пример — это батарейка, в которой используется электролит. Примеров использования батарей и аккумуляторов тоже достаточно: они используются в автомобилях, ноутбуках, мобильных телефонах, планшетах и так далее.
Напомним, что помимо проводников, существуют такие тела, как полупроводники и диэлектрики. Как вы знаете, диэлектрики используются для изоляции проводки или электроприборов. Полупроводники представляют довольно большой интерес, поскольку их проводимостью достаточно легко управлять, а это открывает большие возможности.
Со всем выше перечисленным мы познакомимся по окончании курса физики десятого класса, и начнем с проводимости металлов.
Мы уже много раз говорили, что электрический ток — это упорядоченное движение заряженных частиц, и всегда утверждали, что в металлах носителями свободных зарядов являются электроны. Дело в том, что за этим утверждением стоят многочисленные опыты разных ученых. Мы рассмотрим несколько таких опытов.
В 1901 году, Эдуард Рикке провел следующий эксперимент: он подключил к электрической цепи металлические цилиндры, плотно прилегающие друг к другу. В центре находился алюминиевый цилиндр, а по краям — медные.
В течение приблизительно одного года через эти цилиндры протекал электрический ток. После окончания эксперимента, все три цилиндра были исследованы на предмет изменения химического состава.
Выяснилось, что никаких изменений не произошло, за исключением очень незначительной диффузии. Это послужило доказательством того, что ток в металлах обусловлен именно движением электронов.
Если бы в движении участвовали какие-то другие частицы (например, ионы кристаллической решетки), то это, неизбежно привело бы к изменению химического состава.
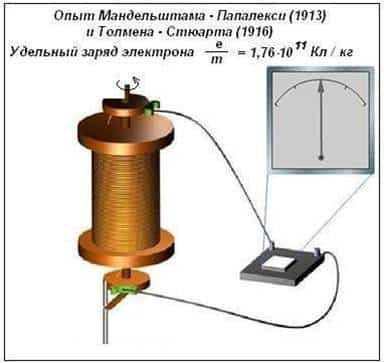
Другой опыт, был проведен в 1912 году учеными Леонидом Мандельштамом и Николаем Папалекси. К катушке, которая могла вращаться вокруг своей оси, был подключен гальванометр при помощи скользящих контактов.
При резкой остановке катушки, гальванометр регистрировал кратковременные токи. Дело в том, что при резкой остановке заряженные частицы какое-то время могли двигаться по инерции относительно проводника (то есть проволоки катушки).
Поскольку сила тока характеризуется зарядом, а инерция — массой частиц, переносимый при торможении заряд пропорционален отношению заряда частиц к их массе.
Из этого эксперимента было определено это соотношение, которое совпало с найденным до этого из других опытов отношением модуля заряда электрона к его массе:
Таким образом, эксперимент Мандельштама и Папалекси еще раз подтвердил, что ток в металлах обусловлен движением электронов. Поэтому, проводимость металлов называют электронной проводимостью.
Вы уже знаете, что электроны в металлах двигаются с постоянной скоростью из-за того, что взаимодействуют с ионами кристаллической решетки. Это приводит к тому, что скорость движения электронов пропорциональна напряженности электрического поля:
В свою очередь, напряженность пропорциональна напряжению. Из чего мы можем заключить, что скорость электронов в проводнике пропорциональна напряжению на концах этого проводника:
Напомним, что не так давно мы выяснили, что скорость также пропорциональна и силе тока:
Из этого мы можем сделать вывод, что ???? ~ ????, а это подтверждает закон Ома.
Теперь, когда мы выяснили, что электрический ток в металлах действительно обусловлен движением электронов, следует обратить внимание на одно из следствий этого явления.
Электроны взаимодействуют с ионами кристаллической решетки и, тем самым нагревают проводник. Но, чем больше проводник нагревается, тем более интенсивными становятся колебания частиц проводника и тем больше они мешают движению электронов.
Следовательно, в металлах существует определенная зависимость их электрического сопротивления от температуры.
Экспериментально была установлена зависимость сопротивления от температуры:
В формуле мы видим коэффициент пропорциональности α, который называется температурным коэффициентом сопротивления. Мы можем немного преобразовать выражение, описывающее зависимость сопротивления от температуры, чтобы дать определение температурному коэффициенту сопротивления:
Итак, температурный коэффициент сопротивления численно равен относительному изменению сопротивления при нагревании на 1 оС. Под относительным изменением сопротивления понимается отношение изменения сопротивления к конечному сопротивлению. Поскольку мы выяснили, что у металлов сопротивление увеличивается с увеличением температуры, можно сделать вывод, что для всех металлов коэффициент α > 0.
- Вспомним, что сопротивление проводника зависит от трех величин: удельное сопротивление материала, из которого сделан проводник, площадь поперечного сечения проводника и его длина:
- Поскольку геометрические размеры проводника при нагревании меняются ничтожно мало, можно сделать вывод, что изменяется удельное сопротивление:
- Из полученной формулы можно сделать вывод, что удельное сопротивление металлов линейно зависит от температуры.
Эта зависимость используется в так называемых термометрах сопротивления. Термометр сопротивления представляет собой проводник, зависимость сопротивления которого от температуры хорошо известна.
Чаще всего используют платиновую проволоку. Измеряя ее сопротивление можно судить о температуре.
Преимущество подобного термометра заключается в том, что он пригоден для измерения температур в значительно более широком диапазоне, чем это возможно, используя жидкостные термометры.
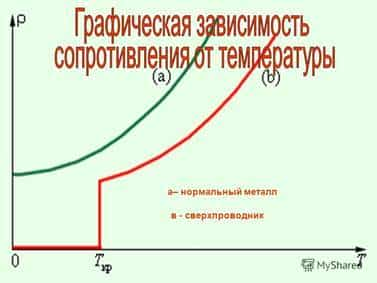
Возникает вопрос: а что будет происходить при очень низких температурах? Этим вопросом еще в 1911 году задался Хейке Камерлинг-Оннес. В качестве опыта, он поместил ртуть в жидкий гелий и наблюдал, как постепенно уменьшается удельное сопротивление с падением температуры.
Однако, когда температура опустилась до четырех целых одной десятой кельвина, сопротивление резко упало до нуля. Такое явление получило название сверхпроводимости, а температура, при которой наступает это состояние, была названа критической температурой.
Явление сверхпроводимости возникает во многих металлах при достаточно низких температурах (около 25 К). Это явление можно объяснить тем, что при таких низких температурах беспорядочное движение электронов становится очень незначительным. Иными словами, они двигаются, не соударяясь с ионами кристаллической решетки, таким образом, не замедляя своего движения и не нагревая проводник.
Конечно, это объяснение существенно упрощено, но оно дает общее представление о том, как возникает явление сверхпроводимости. Тот факт, что в состоянии сверхпроводимости проводники не нагреваются, открывает большие перспективы.
Если найти способ создать явление сверхпроводимости при обычных (комнатных) температурах, то можно было бы передавать электроэнергию по проводам без всяких потерь.
Сверхпроводимость используется для создания электромагнитов, которые могут создавать магнитное поле в течение длительного времени без всяких потерь энергии.
Также, сверхпроводящие магниты используются в ускорителях элементарных частиц (таких как Большой Адронный Коллайдер). В 1986 году удалось создать некоторые соединения, переходящие в состояние сверхпроводимости при температурах около 100 К.
На сегодняшний день, нет известных соединений, в которых бы наблюдалась сверхпроводимость при температуре выше 138 К (при нормальном давлении).
Рассмотрим еще один интереснейший эффект явления сверхпроводимости, который получил название эффекта Мейснера. Поместим два керамических цилиндра в специальную емкость и зафиксируем их.
При температуре 93 К эти цилиндры становятся сверхпроводящими. Для охлаждения можно использовать жидкий азот. Если теперь поднести к цилиндрам достаточно сильный магнит, то он зависнет над ними. Как вы знаете из курса физики девятого класса, при изменении магнитного потока через контур, возникает индукционный ток.
В обычных условиях, этот ток был бы незначительным и кратковременным. Однако, в состоянии сверхпроводимости, сопротивление равно нулю, поэтому, ток продолжает течь по цилиндрам. Этот ток создает магнитное поле, которое и вызывает силы отталкивания между цилиндрами и магнитом.
Если же теперь мы поместим над цилиндрами магнит в виде колесика и раскрутим его, то он будет продолжать крутиться до тех пор, пока цилиндры находятся в состоянии сверхпроводимости. Заметим, что магнит крутится, не касаясь цилиндров и не нагреваясь, то есть никаких потерь энергии не происходит.
Тем не менее, нет возможности получить сколь угодно большой ток в сверхпроводниках, поскольку определенное критическое значение силы тока разрушает состояние сверхпроводимости.
Однако, конструкции, основанные на подобном принципе, могли бы существенно усовершенствовать электродвигатели и генераторы, значительно упростить устройства для аккумулирования энергии и многое другое. Поэтому, сегодня получение сверхпроводимости при комнатных температурах является одной из очень важных задач в физике.
Электронная проводимость металлов
>>> Перейти на мобильный размер сайта >>>
Учебное особие по физике
Электронная проводимость металлов была впервые экспериментально доказана немецким физиком Э.Рикке в 1901 г.
Через три плотно прижатых друг к другу отполированных цилиндра — медный, алюминиевый и снова медный — длительное время (в течение года) пропускали электрический ток. Общий заряд, прошедший за это время, был равен 3.5·106 Кл.
Поскольку массы атомов меди и алюминия существенно отличаются друг от друга, то массы цилиндров должны были бы заметно измениться, если бы носителями заряда были ионы.
Результаты опытов показали, что масса каждого из цилиндров осталась неизменной.
В соприкасающихся поверхностях были обнаружены лишь незначительные следы взаимного проникновения металлов, которые не превышали результатов обычной диффузии атомов в твердых телах.
Следовательно, свободными носителями заряда в металлах являются не ионы, а такие частицы, которые одинаковы и в меди, и в алюминии. Такими частицами могли быть только электроны.
Прямое и убедительное доказательство справедливости этого предположения было получено в опытах, поставленных в 1913 г. Л. И. Мандельштамом и Н. Д. Папалекси и в 1916 г. Т. Стюартом и Р. Толменом.
На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга (рис. 1). К концам дисков с помощью скользящих контактов присоединяют гальванометр.
Рис. 1
Катушку приводят в быстрое вращение, а затем резко останавливают.
После резкой остановки катушки свободные заряженные частицы будут некоторое время двигаться вдоль проводника по инерции, и, следовательно, в катушке возникнет электрический ток.
Ток будет существовать короткое время, так как из-за сопротивления проводника заряженные частицы тормозятся и упорядоченное движение частиц прекращается.
Направление тока говорит о том, что он создается движением отрицательно заряженных частиц. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе, т.е. . Поэтому, измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение . Оно оказалось равным 1,8·1011 Кл/кг. Эта величина совпадает с отношением заряда электрона к его массе, найденным ранее из других опытов.
Таким образом, электрический ток в металлах создается движением отрицательно заряженных частиц электронов. Согласно классической электронной теории проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), металлический проводник можно рассматривать как физическую систему совокупности двух подсистем:
- свободных электронов с концентрацией ~ 1028 м-3 и
- положительно заряженных ионов, колеблющихся около положения равновесия.
Появление свободных электронов в кристалле можно объяснить следующим образом.
Рис. 2
При объединении атомов в металлический кристалл слабее всего связанные с ядром атома внешние электроны отрываются от атомов (рис. 2).
Поэтому в узлах кристаллической решетки металла располагаются положительные ионы, а в пространстве между ними движутся электроны, не связанные с ядрами своих атомов. Эти электроны называются свободными или электронами проводимости.
Они совершают хаотическое движение, подобное движению молекул газа. Поэтому совокупность свободных электронов в металлах называют электронным газом.
Если к проводнику приложено внешнее электрическое поле, то на беспорядочное хаотическое движение свободных электронов накладывается направленное движение под действием сил электрического поля, что и порождает электрический ток.
Скорость движения самих электронов в проводнике — несколько долей миллиметра в секунду, однако возникающее в проводнике электрическое поле распространяется по всей длине проводника со скоростью, близкой к скорости света в вакууме (3·108 м/с).
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электроны под влиянием постоянной силы, действующей со стороны электрического поля, приобретают определенную скорость упорядоченного движения (ее называют дрейфовой).
Эта скорость не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решетки электроны передают кинетическую энергию, приобретенную в электрическом поле, кристаллической решетке. В первом приближении можно считать, что на длине свободного пробега (это расстояние, которое электрон проходит между двумя последовательными столкновениями с ионами) электрон движется с ускорением и его дрейфовая скорость линейно возрастает со временем
В момент столкновения электрон передает кинетическую энергию кристаллической решетке. Потом он опять ускоряется, и процесс повторяется. В результате средняя скорость упорядоченного движения электронов пропорциональна напряженности электрического поля в проводнике и, следовательно, разности потенциалов на концах проводника, так как , где l — длина проводника.
Известно, что сила тока в проводнике пропорциональна скорости упорядоченного движения частиц
а значит, согласно предыдущему, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.
Однако в рамках этой теории возникли трудности. Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (), между тем, согласно опыту, ~ Т.
Кроме того, теплоемкость металлов, согласно этой теории, должна быть значительно больше теплоемкости одноатомных кристаллов. В действительности теплоемкость металлов мало отличается от теплоемкости неметаллических кристаллов.
Эти трудности были преодолены только в квантовой теории.
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при -269°С) удельное сопротивление скачком уменьшается (рис. 3) практически до нуля. Это явление обращения электрического сопротивления в нуль Г. Камерлинг-Оннес назвал сверхпроводимостью.
Рис. 3
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012К, самое высокое у ниобия — 9К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
Вещества в сверхпроводящем состоянии обладают необычными свойствами:
- электрический ток в сверхпроводнике может существовать длительное время без источника тока;
- внутри вещества в сверхпроводящем состоянии нельзя создать магнитное поле:
- магнитное поле разрушает состояние сверхпроводимости. Сверхпроводимость — явление, объясняемое с точки зрения квантовой теории. Достаточно сложное его описание выходит за рамки школьного курса физики.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий.
Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах.
Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
В настоящее время в линиях электропередачи на преодоление сопротивления проводов уходит 10 — 15% энергии. Сверхпроводящие линии или хотя бы вводы в крупные города принесут громадную экономию. Другая область применения сверхпроводимости — транспорт.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100К, то есть при температуре выше температуры кипения азота.
Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
Конспект урока физики "Электронная проводимость металлов. Зависимость сопротивления проводника от температуры. Сверхпроводимость
10 класс. Электронная
проводимость металлов. Зависимость
-
сопротивления проводника от температуры. -
Сверхпроводимость. - ЦЕЛЬ УРОКА:
разъяснить физическую природу электрической -
проводимости металлов с точки зрения электронной -
теории; объяснить с точки зрения электронной теории -
зависимость сопротивления от температуры; дать -
понятие о сверхпроводимости. -
ХОД УРОКА
І. Объяснение нового материала (лекция с
элементами беседы).

Мы уже знаем, что электрический ток в
металлических проводниках – это ???
ОТВЕТ: упорядоченное
движение свободных электронов между ионами кристаллической решетки.
Приведем
факты, подтверждающие справедливость сказанного и опираясь на эти факты,
углубим имеющиеся представления об электронной проводимости металлов.
ОПЫТ К.РИККЕ. немецкий физик К. Рикке в 1901 г. проделал следующий
опыт Три предварительно взвешенных цилиндра (два медных и один
алюминиевый) Рикке сложил отшлифованными торцами так, что алюминиевый
оказался между медными.
Затем цилиндры были подключены в цепь постоянного
тока через них в течение года проходил большой ток питавший
городскую трамвайную сеть.
За это время через цилиндры прошел электрический
заряд, равный приблизительно 3,5 млн Кл.
Вторичное взвешивание цилиндров, проводившееся с точностью до 0,03 мг,
показало, что масса цилиндров в результате опыта не изменилась.
При исследовании
соприкасающихся торцов под микроскопом было установлено, что имеются лишь
незначительные следы проникновения металлов, которые не превышают результатов
обычной диффузии атомов в твердых телах.
Результаты опыта свидетельствовали о
том, что в переносе заряда в металлах ионы не участвуют.
 Для выяснения природы носителей тока в металлах физики
Для выяснения природы носителей тока в металлах физики
Мандельштам и Папалекси провели в 1913 году оригинальный опыт. Идея опыта
сводилась к тому, чтобы обнаружить электрический ток при внезапной остановке
быстро движущегося проводника. При резком торможении носители тока будут
продолжать двигаться по инерции. Поэтому в замкнутой цепи появится
кратковременный ток, который можно будет обнаружить с помощью гальванометра. По
направлению тока можно определить знак движущихся зарядов. Было доказано, что
носителями тока в металлическом проводнике могут быть только электроны.
Немецкий физик П. Друде в 1900 г. Опираясь на представления
об электрическом токе в металлах как упорядоченном движении свободных
электронов между ионами кристаллической решетки под действием внешнего
электрического поля, создал теорию электропроводности металлов. В основе
этой теории лежат следующие допущения:
- ·
свободные электроны в
металле ведут себя как молекулы идеального газа; «электронный газ» подчиняется
законам идеального газа; - ·
движение свободных
электронов в металле подчиняется законам классической механики Ньютона; - ·
свободные электроны в
процессе их хаотического движения сталкиваются не между собой (как молекулы
идеального газа), а с ионами кристаллической решетки; - ·
при столкновении
электронов с ионами электроны передают ионам свою кинетическую энергию
полностью.
Теория Друде – весьма упрощенное представление об
электронной проводимости в металле как об идеальном электронном газе. Она не
раскрывает природу зависимости электросопротивления от абсолютной температуры.
И все же на основе этой теории удалось объяснить основные законы электрического
тока в металлах.
Давайте вспомним, как связаны между собой скорость упорядоченного
движения электронов в металле и сила тока?
ОТВЕТ: ‹ν› = J/enS
Каждый проводник
ограничивает силу тока в цепи. Но каков механизм этого явления? Какова природа
электрического сопротивления металлических проводников?
Давайте еще раз
прочтем основные допущения теории и попробуем ответить на вопрос, что же
происходит в металлическом проводнике под действием внешнего электрического
поля?
ОТВЕТ: с точки зрения
электронной теории Друде, электроны, дрейфуя под действием внешнего
электрического поля, вдоль поликристаллического проводника сталкиваясь с ионами
кристаллической решетки, передают им полученную от поля энергию. В результате
после каждого из соударений скорость их упорядоченного движения под действием
внешнего электрического поля делается равной нулю. Это приводит к ограничению
протекающего по проводнику тока.
- СДЕЛАЕМ ВЫВОД: чем
же обусловлено электрическое сопротивление металлов? - ОТВЕТ: с точки зрения электронной теории
электрическое сопротивление металлов обусловлено соударениями свободных
электронов с ионами кристаллической решетки. - Скажите, а какие
процессы происходят в твердом теле при повышении температуры? - ОТВЕТ: при повышении температуры твердого тела
увеличивается интенсивность колебаний ионов кристаллической решетки.
А теперь представьте кристаллическую решетку
металлического проводника: увеличение температуры приводит к увеличению
интенсивности колебаний ионов решетки, при этом под действием внешнего
электрического поля в проводнике упорядоченно движется электроны. К чему это
приводит?
ОТВЕТ: чем выше температура тела, в данном случае
проводника, тем интенсивнее колебания ионов кристаллической решетки и тем чаще
электроны сталкиваются с ними.
СЛЕДОВАТЕЛЬНО: с
повышением температуры сопротивление металлических проводников …..
УВЕЛИЧИВАЕТСЯ.
ОПЫТ: стальная спираль ( d = 0,3 мм, ℓ = 0,5 м)
включается в цепь последовательно с индикатором – автомобильной лампочкой ( 6
В, 21 Вт). Спираль нагревают спиртовкой.
- ВЫВОД: яркость
свечения лампы, включенной последовательно - со стальной спиралью, уменьшается при нагревании
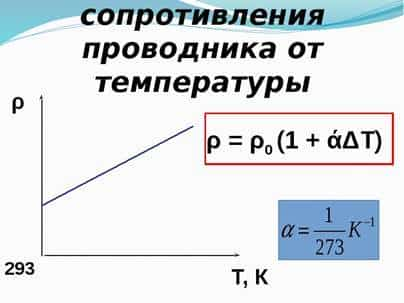
спирали и увеличивается при ее охлаждении. - Экспериментально установлено, что для большинства чистых
металлов с ростом температуры сопротивление увеличивается приблизительно по
линейному закону - R = R0 ( 1 + αΔТ), где R0
– сопротивление проводника при 0° С; α – температурный
коэффициент сопротивления, который показывает изменение сопротивления
проводника по сравнению с сопротивлением при 0° С. - α = ( R — R0)/ R0ΔТ.
- Температурные коэффициенты сопротивления чистых металлов мало
отличаются друг от друга и примерно равны 1/273 К-1≈ 0,004 К-1
У сплавов могут быть значения больше или меньше.
Зависимость сопротивления металлических проводников от температуры используется
при устройстве термометров (термосопротивлений). (слайд).
Преимущества таких
термометров высокая точность (до 0,001К) и возможность измерения ими высоких и
очень низких температур. Так платиновым термометром можно измерять температуру
от -269°С до 1063°С.
- Мы уже знаем что с понижением температуры сопротивление
металлических проводников уменьшается. - ВОПРОС:
что произойдет с сопротивлением, если температура проводника будет приближаться
к абсолютному нулю? - ОТВЕТ: сопротивление будет уменьшаться.
На этот вопрос дал ответ голландский физик Г. Камерлинг — Оннес.
ВОПРОС: что обнаружил Камерлинг – Оннес при постепенном охлаждении ртути?
 ОТВЕТ: в
ОТВЕТ: в
1911 году голландский физик Г. Камерлинг – Оннес обнаружил, что при
постепенном охлаждении сопротивление ртути уменьшается по линейному закону
только до температуры 4,15 К, а затем исчезает . Это явление получило название
сверхпроводимости.
- ЗАПОМНИ: температуру, при которой ряд веществ переходит в
- сверхпроводящее состояние называют
критической. - ВОПРОС: какие вещества, кроме ртути обладают
свойством -
сверхпроводимости? - ОТВЕТ: сверхпроводимость была обнаружена у свинца,
цинка, олова, алюминия и других металлов, а также у некоторых сплавов. - ВОПРОС: какими свойствами обладают вещества в
сверхпроводящем состоянии?
 ОТВЕТ: 1) в сверхпроводящем состоянии вещества
ОТВЕТ: 1) в сверхпроводящем состоянии вещества
обладают чрезвычайно интересными свойствами. Если в кольцевом проводнике, находящемся
в сверхпроводящем состоянии, создать ток, а затем отключить источник тока, то
сила этого тока не изменяется неограниченно долго.
2) внутри
сверхпроводника невозможно создать магнитное поле. Внешнее магнитное поле не
проникает внутрь проводника, поскольку при любом изменении магнитного потока в
сверхпроводниках возникают индукционные токи, которые по закону Ленца компенсируют
эти изменения.
3)
магнитное поле разрушает состояние сверхпроводимости. Чем сильнее
сверхпроводник охлажден ниже температуры перехода в сверхпроводящее состояние,
тем сильнее и «критическое» магнитное поле, при котором исчезает
сверхпроводимость. Магнитным полем, разрушающим сверхпроводимость, может быть и
поле самого тока в сверхпроводнике.
ВОПРОС: где применяют сверхпроводящие материала?
·
Проволоку из
сверхпроводящего материала используют для изготовления соленоидов. Пропуская
через них большой ток, можно получить сильные магнитные поля. Такие соленоиды
почти не рассеивают тепла, в то время как в соленоидах с обычной (
несверхпроводящей) обмоткой при получении сильных полей выделяется огромное
количество тепла.
- ·
Разрушение
сверхпроводимости сильными магнитными полями делает возможным создание
переключающих устройств – криотронов, которые служат в качестве6 элементов
памяти счетных машин; - ·
В ряде сверхпроводников (
сплавы Nв – Sn, Ti – V) разрушение сверхпроводимости наступает в очень сильных
магнитных полях; такие сверхпроводники могут быть использованы для изготовления
сверхпроводящих магнитов; - ·
Сверхпроводники нашли
применение при создании семейства сверхчувствительных измерительных приборов (
сверхпроводящие квантовые интерференционные детекторы), которые используют в
медико-биологических исследованиях ( с их помощью удается определить
характеристики очень слабых магнитных полей, возникающих при работе сердца и
мозга).
Электронная теория проводимости металлов не смогла
объяснить явление сверхпроводимости. Это было объяснено с позиций квантовой
физики.
ІІ. РЕШЕНИЕ
ЗАДАЧ.
1. Сопротивление медного провода при 20°С равно
50 Ом. Определить
- его сопротивление
при — 30°С ( α = 0,004 К-1). - R1 = R0 ( 1 + αt1),
- R2 = R1 (
1 + αt2)/ αt1 - R2 = R0 ( 1 + αt2),
R2 = 40,74 Ом. - 2. Сопротивление
вольфрамовой нити лампы накаливания при - температуре 20°С
равно 20 Ом, а при 3000°С равно 250 Ом. - Определить
температурный коэффициент сопротивления вольфрама. - R1 = R0 (1 + αt1),
- R2 = R0 (1 + αt2),
- R1/ R2 = (1 + αt1)/ (1 + αt2),
- α = (R2 — R1 ) /R1t2 – R2t1
Электрический ток в металлах: подробное объяснение (формулы)
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток – это упорядоченный поток носителей электрического заряда. Носители – это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в “облако” хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости.
В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда.
Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как “ро”). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр.
Удельное сопротивление – это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10-8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10-8 Ом .
В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10-8 |
| Медь | 1.72*10-8 |
| Алюминий | 2.82*10-8 |
| Вольфрам | 5.6*10-8 |
| Железо | 10*10-8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью “свободным”, поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).
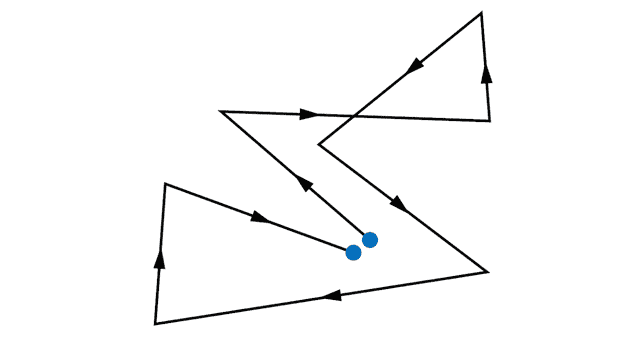 Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E – сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с иономкристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию.
Однако замедленный электрон не остается в состоянии покоя – он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д.
Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).
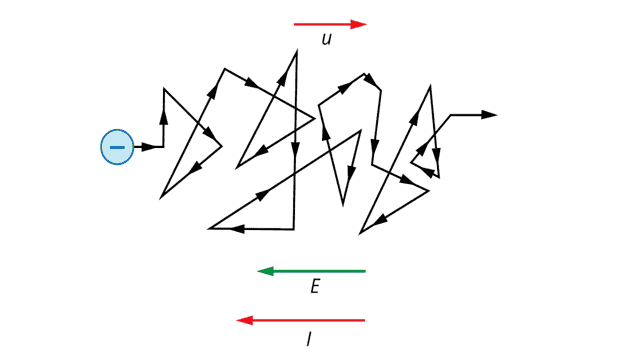 Рис. 2. Дрейф электрона под действием внешнего электрического поля
Рис. 2. Дрейф электрона под действием внешнего электрического поля
В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).
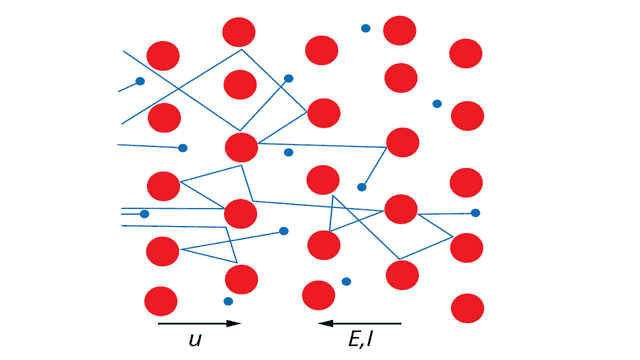 Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ – средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки.
Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10-4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 106 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями.
Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно.
Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток.
Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика – несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это.
Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь.
Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Классическая электронная теория проводимости Друде-Лоренца
Теория Друде была разработана в 1900 году, через три года после открытия электрона. Затем теория была доработана Лоренцом, и сейчас она является классической и актуальной теорией проводимости металлов.
Электронная теория Друде-Лоренца
Согласно теории, носителями тока в металлах являются свободные электроны.
Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют «электронный газ».
Двигаясь в металле, электроны соударяются между собой и с кристаллической решеткой (это и есть проявление электрического сопротивления проводника). Между соударениями электроны, по аналогии с длиной свободного пробега молекул идеального газа, успевают преодолеть средний путь λ.
Без действия электрического поля, ускоряющего электроны, кристаллическая решетка и электронный газ стремятся к состоянию теплового равновесия.
Приведем основные положения теории Друде:
- Взаимодействие электрона с другими электронами и ионами не учитывается между столкновениями.
- Столкновения являются мгновенными событиями, внезапно меняющими скорость электрона.
- Вероятность для электрона испытать столкновение за единицу времени равна 1τ.
- Состояние термодинамического равновесия достигается благодаря столкновениям.
Важно.
Несмотря на множество допущений, теория Друде-Лорецна хорошо объясняет эффект Холла, явление удельной проводимости и теплопроводность металлов. Именно поэтому она актуальна по сей день, хотя ответы на многие вопросы (например, почему в металле существуют свободные ионы и электроны) смогла дать только квантовая теория твердого тела.
В рамках теории Друде объясняется сопротивление металлов. Оно обусловлено соударениями электронов с узлами кристаллической решетки.
- Выделение тепла, согласно закону Джоуля-Ленца, также происходит по причине соударения электронов с ионами решетки.
- Теплопередача в металлах также осуществляется электронами, а не кристаллической решеткой.
- Терия Друде не объясняет многих явлений, как например сверхпроводимость, и не применима в сильных магнитных полях, в слабых магнитных полях может терять применимость из-за квантовых явлений.
- Среднюю скорость электронов можно вычислить по формуле для идеального газа:
- v=8kTπm
- Здесь k — постоянная Больцмана, T — температура металла, m — масса электрона.
- При включении внешнего электрического поля, на хаотичное движение частиц «электронного газа» накладывается упорядоченное движение электронов под действием сил поля, когда электроны начинают упорядоченно двигаться со средней скоростью u. Величину этой скорости можно оценить из соотношения:
- j=nqu,
- где j — плотность тока, n — концентрация свободных электронов, q — заряд электрона.
- При больших плотностях тока рассчеты дают следующий результат: средняя скорость хаотичного движения электронов во много раз (≈108) больше скорости упорядоченного движения под действием поля. При вычислении суммарной скорости полагают, что
- u→+v→≈v→
Формула Друде
- Формула Друде выводится из кинетического уравнения Больцмана и имеет вид:
- σ=nq2τm*
- Здесь m* — эффективная масса электрона, τ — время релаксации, то есть время, за которое электрон «забывает» о том, в какую сторону двигался после соударения.
- Друде вывел закон Ома для токов в металле:
- j=σ·E→
Опыт Толмена и Стюарта
В 1916 году опыт Толмена и Стюарта дал прямое доказательство тому, что носителями тока в металлах являются электроны.
Суть опыта была в следующем.
Опыт Толмена и Стюарта
Проводящая катушка с проводом длиной L вращалась вокруг своей оси с большой скоростью, а ее концы были замкнуты на гальванометр. Когда катушку резко тормозили, свободные электроны в металле продолжали двигаться по инерции, и гальванометр регистрировал импульс тока.
Считая, что свободные электроны подчиняются законам механики Ньютона, можно записать, что при остановке проводника электрон приобретает ускорение v' (в катушке направлено вдоль проводов). При этом на электрон действует сила, направленная противоположно ускорению.
- F=-mv'
- Под воздействием этой силы электрон ведет себя так, как если бы на него действовало поле E=-mv'q. Эдс, возникающую в катушке при торможении можно записать, как:
- ε=∫LEdl=-mv'q∫Ldl=-mv'qL
- Считая, что ускорение одинаково в каждом витке, можно записать закон Ома для катушки, а затем вычислить заряд, проходящий в ней за время dt:
- IR=-mv'qL
- dq=Idt=-mLdvqRdtdt=-mLdvqR
- Заряд, прошедший от момента начала торможения до остановки:
- q=-mLqR∫v00dv=-mLv0qR
- Опыт Толмена и Стюарта получил хорошее согласование с теорией, полученное экспериментально отношение qmсоответствовало отношению заряда электрона к его массе.
Пример
- При T=300К вычислите среднюю скорость теплового движения свободных электронов.
- Решение.
- Вычислим среднюю скорость, применяя формулу для идеального газа:
- v=8kTπm
- k=1,38·10-23 ДжК
- m=9,31·10-31кг
- Подставляем значения и вычисляем:
- v=8·1,38·10-23·3·1023,14·9,31·10-31≈105 мс






