- Что такое прогиб балки?
- Метод начальных параметров
- Расчет прогибов балки
- Реакции опор
- Система координат
- Распределенная нагрузка
- Учет внешней нагрузки
- Формулы прогибов
- Вычисление прогиба
- Расчет балки онлайн — Калькулятор балок перекрытия из дерева
- Инструкция к калькулятору
- Расчет балок перекрытия
- Виды балок
- Подбор сечения балки
- Расчет балки – Пример
- Длина балки
- Определение расчетной нагрузки
- Максимальный изгибающий момент
- Требуемый момент сопротивления
- Момент сопротивления балки перекрытия
- Расчет балки на прочность
- Расчет балки на прогиб (изгиб)
- Конечные параметры балки
- Методика расчета балок перекрытия из клееного бруса и отесанного бревна
- Полный расчет балки на прочность и жесткость
- Определение опорных реакций
- Построение эпюр Q и М
- Подбор сечения двутавровой балки
- Проверка сечения балки по касательным напряжениям
- Расчет балки
- Расчёт металлической балки онлайн (калькулятор)
- Расчет балок на прочность онлайн
- Онлайн калькулятор расчет балки на прочность
- Виды вероятных нагрузок

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
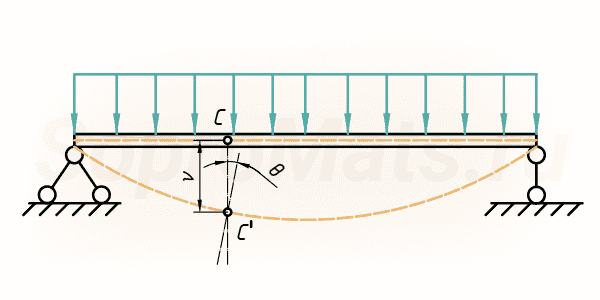
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости.
Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет.
Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
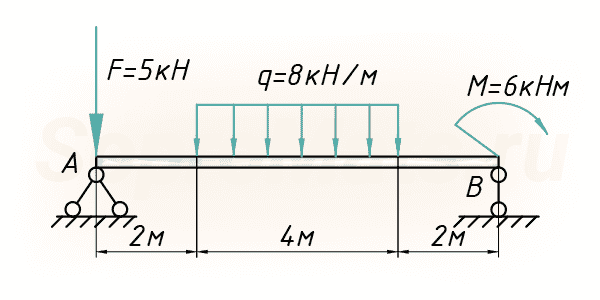
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
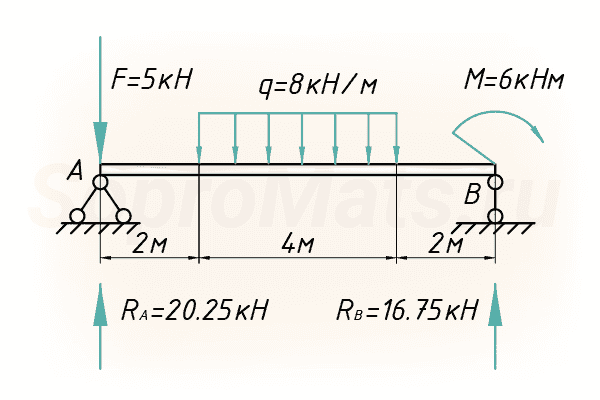
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
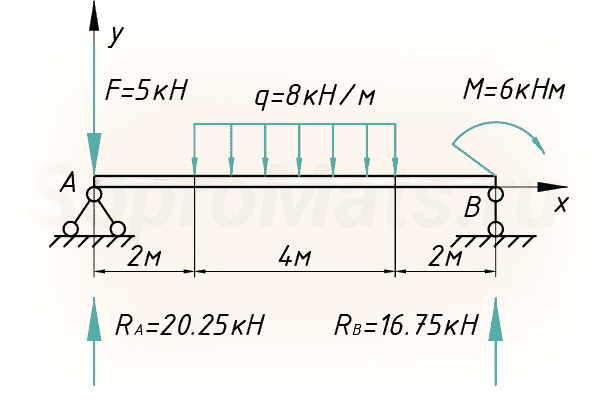
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
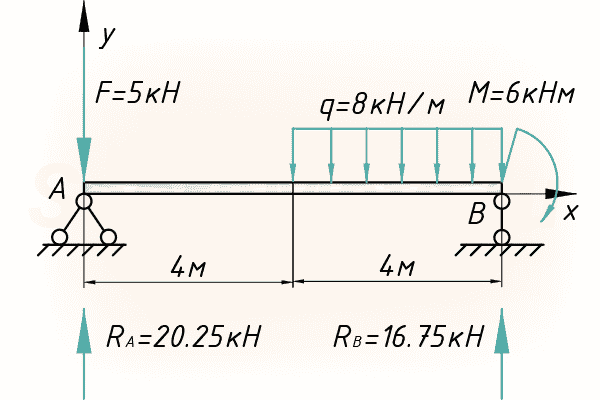
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
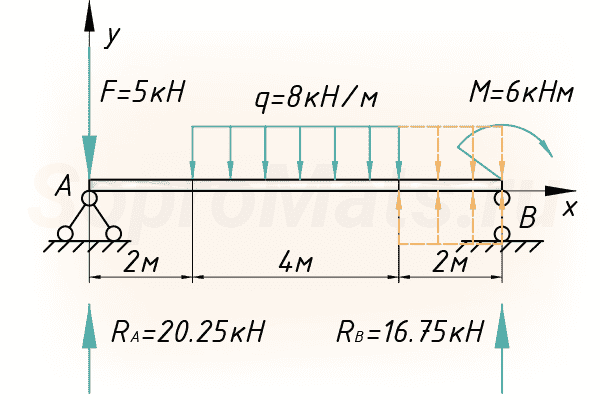
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
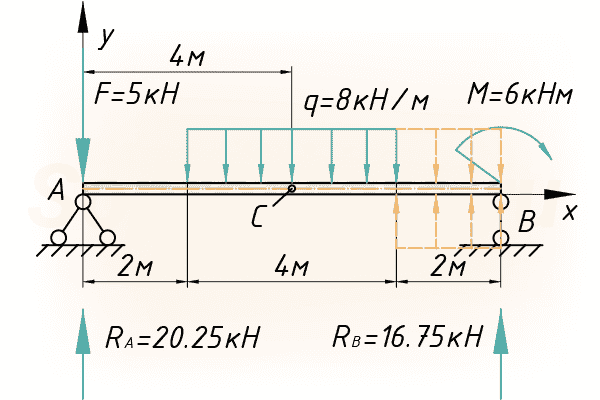
- Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
- [ { V }_{ A }=0quad приquad x=0 ]
- [ { V }_{ B }=0quad приquad x=8м ]
- Записываем уравнение метода начальных параметров для сечения C:
- [ E{ I }_{ z }{ V }_{ C }=… ]
- Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
- [ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … ]
- Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
- [ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ heta }_{ A }cdot 4+… ]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:
- Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

- Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:
- Все сосредоточенные моменты нужно умножать дробь:
[ Mcdot frac { { x }^{ 2 } }{ 2 } ]
- Все сосредоточенные силы нужно умножать дробь:
[ Fcdot frac { { x }^{ 3 } }{ 6 } ]
- Начало и конец распределенных нагрузок нужно умножать на дробь:
[ qcdot frac { { x }^{ 4 } }{ 24 } ]
Формулы прогибов
С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:
[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ heta }_{ A }cdot 4+frac { { R }_{ A }cdot { 4 }^{ 3 } }{ 6 } -frac { Fcdot { 4 }^{ 3 } }{ 6 } -frac { qcdot { 2 }^{ 4 } }{ 24 } ]
В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.
- Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:
- [ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ heta }_{ A }cdot 8+frac { { R }_{ A }cdot { 8 }^{ 3 } }{ 6 } -frac { Fcdot { 8 }^{ 3 } }{ 6 } -frac { qcdot 6^{ 4 } }{ 24 } +frac { qcdot 2^{ 4 } }{ 24 } =0 ]
- Упрощаем уравнение:
- [ E{ I }_{ z }{ heta }_{ A }cdot 8+874.67=0 ]
- Выражаем угол поворота:
[ { heta }_{ A }=-frac { 874.67 }{ 8E{ I }_{ z } } =-frac { 109.33кН{ м }^{ 2 } }{ E{ I }_{ z } } ]
Подставляем это значение в наше первое уравнение и находим искомое перемещение:
[ E{ I }_{ z }{ V }_{ C }=frac { -109.33cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +frac { { R }_{ A }cdot { 4 }^{ 3 } }{ 6 } -frac { Fcdot { 4 }^{ 3 } }{ 6 } -frac { qcdot { 2 }^{ 4 } }{ 24 } =-frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } ]
Вычисление прогиба
Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:
[ { V }_{ C }=-frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } =-frac { 280cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 7080{ см }^{ 4 } } =-2см ]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
Источник: https://SoproMats.ru/sopromat/raschet-progiba-balki
Расчет балки онлайн — Калькулятор балок перекрытия из дерева

Балка – это элемент строительных несущих конструкций, который широко используется для возведения межэтажных перекрытий. Перекрытия, в свою очередь, предназначены для разделения по высоте смежных помещений, а также принятия статических и динамических нагрузок от находящихся на нем предметов интерьера, оборудования, людей и т.д.
В большинстве случаев, для частного домостроения используются деревянные балки из цельного бруса, отесанного бревна, клееных досок или шпона. Эти материалы, при правильном подборе параметров, способны обеспечить необходимую прочность и жесткость основания, что является залогом долговечности постройки.
Мы предлагаем вам выполнить онлайн расчет балки перекрытия на прочность и изгиб, подобрать её сечение и определить шаг между балками. Также вы получите набор персональных чертежей и 3D-модель для лучшего восприятия возводимой конструкции. Программа учитывает СНиП II-25-80 (СП 64.13330.2011) и другие справочные источники.
Содержание
Инструкция к калькулятору
Наш сервис предоставляет на выбор два вида расчета однопролетных балок перекрытия.
В первом случае, вам предлагается рассчитать сечение балки при известном шаге между ними, во втором случае, вы можете узнать рекомендуемое значение шага между балками при выбранных характеристиках сечения. Разберем работу калькулятора на примере, когда ваша задача заключается в нахождении сечения балки.
Для расчета вам понадобится знать ряд обязательных начальных параметров. В первую очередь это характеристики самой балки:
- ширина сечения (толщина), мм;
- длина пролета балки (на изображении BLN), м;
- вид древесины (сосна, ель, лиственница…);
- класс древесины (1/К26, 2/К24, 3/К16);
- пропитка (есть, нет).
В случае, если вы не знаете толщину предполагаемой балки, в первом блоке следует выбрать пункт «Известно соотношение высоты сечения балки к её ширине — h/b» и указать значение 1,4. Эта наиболее оптимальная величина, которая получена эмпирическим методом и указывается во многих справочниках.
Затем нужно указать условия, в которых будет эксплуатироваться перекрытие:
- температурный режим (< 35 °C .. > 50 °C);
- влажностный режим;
- присутствуют постоянные повышенные нагрузки или нет.
После этого, сконфигурируйте конструкцию и заполните поля калькулятора:
- длина стены дома по внутренней стороне, м;
- шаг между балками, см;
- полная длина балки (на изображении BFL), м;
- нагрузка на балку, кг/м2 ;
- предельный прогиб в долях пролета.
- При необходимости впишите стоимость одного кубометра древесины, для того чтобы узнать общую стоимость всех пиломатериалов.
- Также, обратим внимание, что обычно шаг балки не делают меньше 0,3 м, так как это нецелесообразно с экономической точки зрения и больше 1,2 м, так как возможен прогиб чернового пола со всеми вытекающими последствиями.
- Когда вы нажмете кнопку «Рассчитать», сервис произведет расчет балки онлайн и выведет на экране рекомендуемые значения сечения подобранной балки.
- Кроме того, в блоке «Результаты расчета» вы сможете узнать:
- параметры балки при расчете на прочность;
- параметры балки при расчете на прогиб;
- максимальный прогиб балки, см.
Расчет балок перекрытия
Самостоятельный расчет деревянной балки перекрытия – это долгое и нудное занятие, которое обязывает вас знать основы инженерных дисциплин и сопромата.
Без определенных навыков и знаний, вручную подобрать материал, рассчитать необходимое сечение или шаг балки – не просто тяжело, а порой и невозможно.
Тем не менее, мы попытаемся вам рассказать об основных характеристиках, которые нужны для вычислений и по какому алгоритму работает наш калькулятор.
Виды балок
В настоящее время, деревянные балки, используемые для изготовления перекрытий, можно разделить на два принципиально разных вида:
Исходя из названия становится понятно, что в первом случае, это будет цельный кусок древесины определенного типа сечения (чаще всего это брус на 2 или 4 канта), во втором случае, это клееная балка из досок или шпона LVL.
Несмотря на низкую стоимость, по ряду объективных причин, деревянные балки из цельной древесины в последнее время используются все реже.
Качественные показатели этого материала значительно уступают клееному дереву: низкий модуль упругости способствует появлению больших прогибов в середине пролета (особенно это становится заметно при расстоянии между несущими стенами более 4 метров), при высыхании на балках появляются продольные трещины, которые приводят к уменьшению момента инерции прогиба, отсутствие пропитки подвергает древесину воздействиям вредителей и гниения.
Благодаря современным технологиям, клееные балки не имеют подобных недостатков.
Их структура однородна и волокна ориентированы по всем направлениям – повышается общая прочность и модуль упругости материала, он получает защиту от растрескивания, а специальная пропитка обеспечивает повышенный уровень пожаробезопасности и устойчивости к влаге. Эти балки разрешено использовать при проемах в 6-9 м и можно рассматривать, как полноценный аналог железному перекрытию.




Подбор сечения балки
Для того чтобы подобрать сечение балки самостоятельно вручную, нужно иметь огромный багаж знаний в сфере сопромата, ведь вам потребуется применять на практике большое количество формул и коэффициентов, поэтому для начинающего мастера это достаточно сложная и не совсем нерациональная задача.
Наш калькулятор должен помочь произвести приблизительный расчет деревянного перекрытия и сэкономить значительное количество времени.
Однако пользователь должен понимать, что ни одна программа не заменит настоящего специалиста, так как принцип работы сервиса построен на обработке стандартных табличных величин и не может учитывать конкретных ситуаций.
Расчет балки – Пример
Алгоритм работы программы для расчета балок основывается на СП 64.13330.2011 (Актуализированная редакция СНиП II-25-80). Для большей наглядности, мы разберем расчет однопролетной балки на прогиб и прочность в примере, кратко описывая основные этапы вычисления и формулы.
Длина балки
- Расчетная длина балки определяется значением длины пролета и запасом для укладывания их на стену.
- Узнать протяженность между пролетами не составляет трудности – с помощью рулетки замерьте расстояние, которые необходимо перекрыть балками, и к полученному числу добавьте величину заделки в «гнезда» равную 300 мм (по 150 мм на сторону) или более.
- В случае, когда вы собираетесь крепить балки на специальные металлические крепления, длина пролета будет равна длине балки.
Определение расчетной нагрузки
Для того чтобы правильно рассчитать нагрузку на деревянную балку, нужно определить все виды оказываемых воздействий на перекрытие.
Величину нагрузки можно узнать двумя путями: использовать СНиП 2.01.
07-85* Нагрузки и воздействия и с его помощью высчитать все необходимые коэффициенты вручную, а затем сложить их, или же можно взять нормативные данные из справочников.
Если вы произведете все расчеты правильно, то первый вариант будет более точен, однако никто не застрахован, что при выполнении долгих громоздких вычислений не будет допущена ошибка.
Поэтому для получения приблизительного расчета, целесообразнее взять стандартные величины и применять их в последующих формулах. Согласно справочникам, для межэтажных перекрытий расчетная нагрузка обычно составляет 400 кг/м2, а для чердаков – 200 кг/м2.
Типовые нагрузки для межэтажных перекрытий — 400 кг/м2 и чердаков – 200 кг/м2 применимы не во всех ситуациях. Если подразумевается, что на основание будет воздействовать ненормально большой вес, например, от тяжелого оборудования – необходимо произвести корректировку начальных параметров.
Максимальный изгибающий момент
- Изгибающий момент – момент внешних сил относительно нейтральной оси сечения балки или другого твёрдого тела, иначе простыми словами, это произведение силы на плечо.
- Максимальный изгибающий момент, соответственно, принимает наибольшее значение, которое может выдержать данное тело без нарушения целостности.
- Если на балку будет действовать равномерно распределенная нагрузка (в калькуляторе реализован именно этот случай), то значение максимального изгибающего момента будет равно:
- q – величина нагрузки на перекрытие;
- l – величина пролета перекрытия.
Требуемый момент сопротивления
Момент сопротивления – это способность материала оказывать сопротивления к изгибу, растяжению или сжатию. Для того чтобы определить это значение для деревянной балки, нужно воспользоваться готовой формулой:
- Мmax – величина максимального изгибающего момента;
- R – величина расчетного сопротивления древесины.
Отдельно нужно рассказать о величине R. Она имеет целый ряд поправочных коэффициентов, которые нужно учитывать при расчете балки, если вы хотите получить максимально точный результат. Полная формула выглядит так:
- Rи – расчетное сопротивление древесины изгибу, подбираемое в зависимости от расчетных значений для сосны, ели и лиственницы при влажности 12% согласно СП 64.13330.2011;
- mп – коэффициент перехода для других пород древесины;
- mд – поправочный коэффициент принимаемый в случае, когда постоянные и временный длительные нагрузки превышают 80% суммарного напряжения от всех нагрузок;
- mт – температурный коэффициент;
- ma – коэффициент принимаемый в случае, когда дерево подвергается пропитке антипиренами;
- γсc – коэффициент срока службы древесины.
- … – существуют другие менее важные коэффициенты, однако при расчетах они практически не используются, так как величина поправки слишком незначительна.
Получается, что по сути, величина R это произведение расчетного сопротивления древесины изгибу и различных поправок. В большинстве случаев для получения ориентировочного результата, эти поправки не учитываются, а значение R принимается равным Rи.
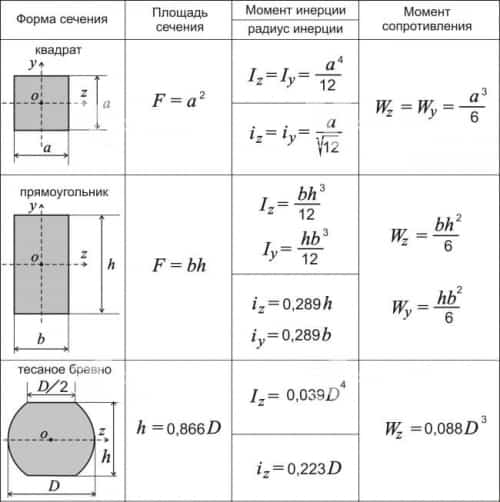
Момент сопротивления балки перекрытия
В зависимости от формы сечения балки (квадрат, прямоугольник, круг, овал…) формулы нахождения фактического момента сопротивления будут отличаться. В наших калькуляторах применяются только два типа профиля: прямоугольный и тесаное бревно. Мы продолжим разбирать алгоритм на примере прямоугольного сечения:
- b – ширина балки;
- h – высота балки.
Расчет балки на прочность
Для того чтобы определить подходит балка по прочности или нет, нужно чтобы момент сопротивления балки перекрытия (W), равнялся или был больше требуемого момента (Wтреб ):
Но вычислить реальный момент сопротивления балки перекрытия мы не можем, так как не известна ее высота. В этом случае нужно или воспользоваться перебором сечений, исходя из условия, что наиболее оптимальное соотношение высоты к ширине 1,4:1, или же просто принять W = Wтреб, в силу того, что мы не нарушаем условий заданной формулы. Также, после этих манипуляций станет известен параметр h.
Расчет балки на прогиб (изгиб)
Методика определения прогиба балки значительно проще. При распределенной нагрузке, применяется формула:
- q – величина нагрузки на перекрытие;
- l – величина пролета перекрытия;
- E – модуль упругости;
- I – момент инерции.
Первые два параметра нам известны, модуль упругости для древесины обычно принимается равным 100 000 кгс/м², хотя это и не всегда так, а момент инерции, в зависимости от формы сечения, рассчитывается по разным формулам. Для прямоугольника:
- b – ширина балки;
- h – высота балки.
Собирая все в кучу, мы получим итоговую формулу расчета прогиба балки:
После того, как вы получите искомое значение, нужно сравнить его с величиной допустимого (предельного) прогиба балки в долях от пролета. Этот параметр устанавливается СНиП II-25-80 «Деревянные конструкции»:
| Элементы конструкций | Максимальный прогиб балки, не более |
| 1. Балки междуэтажных перекрытий | L/250 |
| 2. Балки чердачных перекрытий | L/200 |
| 3. Перекрытия при наличии стяжки/штукатурки | L/350 |
Например, для межэтажных перекрытий при длине пролета равной 400 см мы получим условие – 400/250, т.е. предельно возможный изгиб в данной ситуации 1,6 см.
Если ваше значение f превышает его, необходимо изменять сечение балки в большую сторону, до тех пор, пока оно не станет меньше величины предельного прогиба.
Конечные параметры балки
После того, как вы подберете сечение при расчете на прочность и прогиб/изгиб, можно будет определить минимально допустимые параметры балки.
Предположим, что при расчете на прочность вы получили сечение – 165х150 мм, а при расчете на прогиб – 239х150 мм. Очевидно, что в подобной ситуации следует выбирать наибольшую величину, то есть значение на прогиб, поскольку если вы сделаете ровно наоборот, перекрытие выдержит нагрузку, но очень сильно деформируется и ни о каком ровном потолке не может быть и речи.
В результате расчета несущей способности деревянной балки, мы используем сечение равное 239х150 мм, но тут сталкиваемся с очередной проблемой – балок такого размера серийно никто не производит.
В этом случае нужно производить округление обязательно в большую сторону, обычно кратно 50 мм, т.е. нам подойдет балка 250х150 мм.
В некоторых ситуациях, можно обратиться к ГОСТ 24454-06, в нем указаны все типовые размеры материалов.
Методика расчета балок перекрытия из клееного бруса и отесанного бревна
Технология расчета балок перекрытия из клееного бруса практически не отличается от изделий из цельной древесины.
Все этапы работы с калькулятором совпадают и никакие дополнительные коэффициенты вводить не нужно, но при самостоятельном вычислении в формулу нахождения величины расчетного сопротивления (R), нужно будет добавить дополнительный коэффициент kw , который учитывает форму и размер поперечного сечения.
Например, для прямоугольных клееных балок принимаются следующие поправки:
| Ширина балки b в см | Коэффициент kw при высоте балки h см | |||||
| 14-50 | 60 | 70 | 80 | 90 | 100 и более | |
| b < 14 | 1,00 | 0,95 | 0,90 | 0,85 | 0,80 | 0,75 |
| b > 14 | 1,15 | 1,05 | 0,95 | 0,90 | 0,85 | 0,80 |
Также для клееных балок из шпона LVL Ultralam, существует более подробная аннотация с характеристиками на сайте производителя, в которой помимо значений величины R, существует подробные характеристики модуля упругости (E) для каждого вида продукции:
| Модуль упругости Е, МПа | ||||
| Rb | Rs | R | X | I |
| 16 000 | 15 600 | 14 000 | 11 000 | 12 700 |
В случае расчета тесаного бревна (лафета), немного изменяются исходные формулы момента сопротивления и момента инерции, так как форма сечения балки отличается от прямоугольной. Помимо этого, есть и отличия в ширине отеса, оно может быть равным половине или трети диаметра, что также приводит к изменению начальных коэффициентов для обеих формул.
| Ширина отеса равна 1/2 диаметра | Ширина отеса равна 1/3 диаметра |
| Момент сопротивления | |
| W = 0,088D3 | W = 0,09781D3 |
| Момент инерции | |
| I = 0,039D4 | I = 0,04611D4 |
Источник: https://kalk.pro/beams/
Полный расчет балки на прочность и жесткость
Задача
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400
Решение
Подготовка расчетной схемы к решению задачи
Определение опорных реакций
- Подробно, пример определения опорных реакций для балки рассмотрен здесь
- А также в нашем видеоуроке:
- Из Σmв=0
Из ΣmА=0
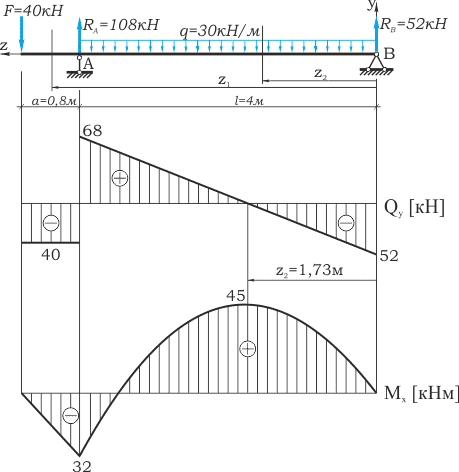
Построение эпюр Q и М
- Примеры построения эпюр поперечных сил Q и изгибающих моментов M для балки
- Наше видео про расчет значений Q и M для построения эпюр
- В пролете балки 0 ≤ z2 ≤ l
QII= — RB+ qz2= -52+30∙z2
QII(z=0)= -52 кН
QII(z=l)= -52+30∙4=68 кН
MII=RB∙z2-qz22/2=52z2-30∙z22/2
MII (z=0)= 0
MII (z=l)= -32 кНм
На консоли l ≤ z1≤ (l+a)
QI= — RB+ ql — RA=-52+30∙4-108=-40 кН
MI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4)
MI (z=l)= -32 кНм
MI (z=l+a)= 0
По этим данным построены эпюры Q и М.
Видео о том, как строить эпюры
Подбор сечения двутавровой балки
Так как Мmах = 45 кНм, то
Wx≥Mmax / [σ] = 45∙103 / 160∙106= 0,281 м3= 281 см3.
- Видео про подбор сечения балки
- По сортаменту выбираем двутавр № 24, для которого Wx = 289 см3, Ix= 3460 см4, Smax = 163 см3, h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h0 = h-2t = 22,1 см.
- Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.
σmax = Mmax / Wx = 45∙103 / 289∙10-6= 156∙106 Па = 156 МПа
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
- Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
- Видео про построение эпюры нормальных напряжений
- Видео про построение эпюры касательных напряжений
Источник: https://isopromat.ru/sopromat/primery-reshenia-zadach/rascet-balki-na-procnost-i-zestkost
Расчет балки
- Заменим распределенную нагрузку равнодействующей
- Q1 = 16·2 = 32кН
- Составим уравнения равновесия для определения реакций опор
- Σ MA = + P · 2 + Q1 · 3 — M — RE · 6= + 412 · 2 + 32 · 3 — 10 — RE · 6=0
- Σ ME = — P · 4 — Q1 · 3 — M + RA · 6= — 412 · 4 — 32 · 3 — 10 + RA · 6=0
- Из этих уравнений находим реакции опор
RA = 292.3кН.
RE = 151.7кН.
Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений
На участке AB: (0 ≤ z1 ≤ 2 м )
Q(z1) = + RA = + 292.3 = 292.333 кН
- M(z1) = + RA · z = + 292.3 · z
- M(0) = 0 кНм
- M(2) = 584.667 кНм
- На участке BC: (2 ≤ z2 ≤ 4 м )
- Q(z2) = + RA — P — q1·(z — 2) = + 292.3 — 412 — 16·(z — 2)
- Q(2) = -119.667 кН
- Q(4) = -151.667 кН
- M(z2) = + RA · z — P·(z — 2) — q1·(z — 2)2/2 = + 292.3 · z — 412·(z — 2) — 16·(z — 2)2/2
- M(2) = 584.667 кНм
- M(4) = 313.333 кНм
- На участке CD: (4 ≤ z3 ≤ 5 м )
Q(z3) = + RA — P — Q1 = + 292.3 — 412 — 32 = -151.667 кН
- M(z3) = + RA · z — P·(z — 2) — Q1·(z — 3) = + 292.3 · z — 412·(z — 2) — 32·(z — 3)
- M(4) = 313.333 кНм
- M(5) = 161.667 кНм
- На участке DE: (5 ≤ z4 ≤ 6 м )
Q(z4) = + RA — P — Q1 = + 292.3 — 412 — 32 = -151.667 кН
- M(z4) = + RA · z — P·(z — 2) — Q1·(z — 3) — M = + 292.3 · z — 412·(z — 2) — 32·(z — 3) — 10
- M(5) = 151.667 кНм
- M(6) = 0 кНм
Максимальный момент в балке составляет Mmax = 585 кНм. По этому значению подбираем сечение балки.
- Условие прочности при изгибе σ = Mmax / W ≤ [σ]
- Отсюда, минимально необходимый момент сопротивления вычисляем по формуле Wmin=Mmax / [σ]
- Подбираем двутавровое сечение при допускаемом напряжении [σ] = 160 МПа
- Wmin=585000 / 160 = 3656.25 см3
Из сортамента выбираем двутавр № с моментом сопротивления W = 0 см3 и площадью A = см2 Максимальные нормальные напряжения в двутавре составляют
- σmax = Mmax/Wx = 585000/0 = 0 МПа
- τmax = Qmax×Sx/b×Ix = 292000×0×10-6/0××10-8 = 0×106 Па = 0 МПа
- τmax = Qmax×Sx'/b×Ix = 292000×0×10-6/0××10-8 = 0×106 Па = 0 МПа,
- Sx'=b×t×(h-t)/2=0×0×(0-0)/2=0 см3.
Максимальные касательные напряжения в двутавре (на центральной оси) составляют Касательные напряжения на границе полки и стенки составляют где статический момент отсеченной полки составляет Эпюры нормальных и касательных напряжений для двутавра: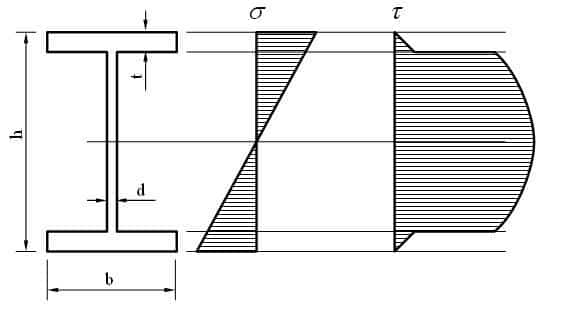
- Подбираем круг. Wmin=585000/160=3656 см3 Момент сопротивления сплошного круглого сечения
- W=π×d3 / 32
d3=32×W / π = 32×3656 / π = 37259 Диаметр сечения будет таким d=33.4 см Площадь сечения
A=π×d2/4=π×33.42/4=875.71 см2
Максимальные нормальные напряжения составляют
σmax = 32×Mmax/π×d3 = 32×585000/π×33.43 = 160.01 МПа
Максимальные касательные напряжения для круга составляют
τmax = 4Qmax/3A = 4×292000/3×875.71×100 = 4.446 МПа
Эпюры нормальных и касательных напряжений для круга: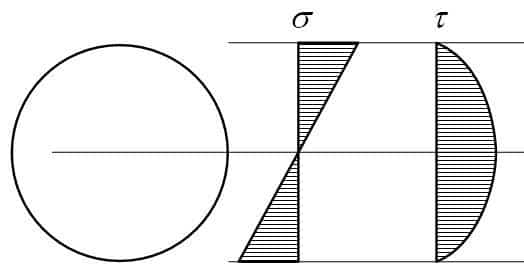
- Подбираем трубу с отношением диаметров α = d/D = 0.9 Wmin=585000 / 160=3656 см3 Момент сопротивления трубчатого сечения
- W=π×D3 ×(1-α4)/32
D3=32×W / π×(1-α4) = 32×3656 / π×(1-0.94)=108341 Диаметр сечения будет таким D=47.7 см
Площадь сечения A=π×D2(1-α2)/4=π×47.72(1-0.92)/4=339.36 см2
Максимальные нормальные напряжения составляют
σmax = 32×Mmax/π×D3×(1-α4) = 32×585000/π×47.73×(1-0.94) = 159.73 МПа
Максимальные касательные напряжения для трубы определим по формуле Журавского
τmax = Qmax×Sx/b×Ix, где b=D-d
Статический момент полусечения
Sx=2R3/3-2r3/3=(D3-d3)/12=(47.73-(47.7×0.9)3)/12=2451 см3
Момент инерции сечения
Ix=π×D4×(1-α4)/64=π×47.74×(1-0.94)/64=87348.48 см4
τmax = 292000×2451×10-6/(47.7-0.9×47.7)×0.01×87348.48-8=0.172×106 Па = 0.172 МПа Эпюры нормальных и касательных напряжений для трубы: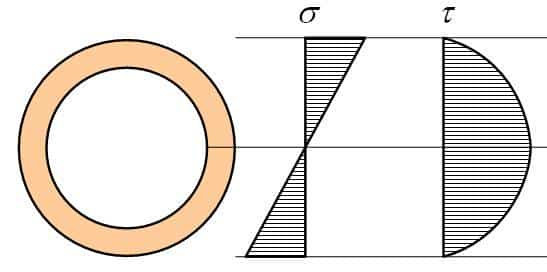
- Подбираем квадрат.Wmin=585000 / 160=3656 см3 Момент сопротивления квадратного сечения
- W=a3/6
- Площадь сечения A=a2=282=784 см2
- Подбираем прямоугольное сечение с отношением сторон h / b=2 Wmin=585000 / 160 = 3656 см3 Момент сопротивления прямоугольного сечения
- W=b×h2 / 6 = b3 × 22 / 6 = b3×0.67
Сторона квадрата будет такой a= 28 см b3=3656 / 0.67=5457 Ширина сечения b=17.6 см, Высота сечения h=b×2=17.6×2=35.2 см
Площадь сечения A=b×h=17.6×35.2=619.52 см2
Максимальные нормальные напряжения составляют
σmax = 6×Mmax/b×h2 = 6×585000/17.6×35.22 = 160.96 МПа
Максимальные касательные напряжения для прямоугольника составляют
τmax = 3Qmax/2A = 3×292000/2×619.52×100 = 7.07 МПа
Эпюры нормальных и касательных напряжений для прямоугольного сечения: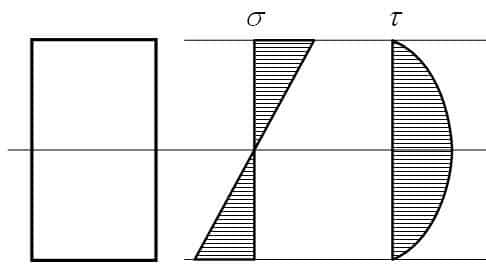
- Записываем уравнения углов поворота и прогибов по методу начальных параметров
- На участке AB: (0 ≤ z1 ≤ 2 м )
- EJ×φ(z) = EJ×φ0 + RA·z2/2
- EJ×v(z) = EJ×v0 + EJ×φ0×z + RA·z3/6
- На участке BC: (2 ≤ z2 ≤ 4 м )
- EJ×φ(z) = EJ×φ0 + RA·z2/2 — P·(z — 2)2/2 — q1·(z — 2)3/6
- EJ×v(z) = EJ×v0 + EJ×φ0×z + RA·z3/6 — P·(z — 2)3/6 — q1·(z — 2)4/24
- На участке CD: (4 ≤ z3 ≤ 5 м )
- EJ×φ(z) = EJ×φ0 + RA·z2/2 — P·(z — 2)2/2 — q1·(z — 2)3/6 + q1·(z — 4)3/6
- EJ×v(z) = EJ×v0 + EJ×φ0×z + RA·z3/6 — P·(z — 2)3/6 — q1·(z — 2)4/24 + q1·(z — 4)4/24
- На участке DE: (5 ≤ z4 ≤ 6 м )
- EJ×φ(z) = EJ×φ0 + RA·z2/2 — P·(z — 2)2/2 — q1·(z — 2)3/6 + q1·(z — 4)3/6 — M· (z — 5)
- EJ×v(z) = EJ×v0 + EJ×φ0×z + RA·z3/6 — P·(z — 2)3/6 — q1·(z — 2)4/24 + q1·(z — 4)4/24 — M· (z — 5)2/2
- Из условий закрепления по этим уравнениям вычислим начальные параметры:
- — начальный угол поворота φ0 = -994.1 кНм2
- — начальный прогиб балки v0 = 0 кНм3
- Найдем углы поворота и прогибы сечений на каждом участке
- На участке AB
- EJ×φ(0) = -994.1 кНм2
- EJ×v(0) = 0 кНм3
EJ×φ(0.5) = -957.5 кНм2
EJ×v(0.5) = -490.9 кНм3
EJ×φ(1) = -847.9 кНм2
EJ×v(1) = -945.3 кНм3
EJ×φ(1.5) = -665.2 кНм2
- EJ×v(1.5) = -1327 кНм3
- EJ×φ(2) = -409.4 кНм2
- EJ×v(2) = -1598 кНм3
- На участке BC
- EJ×φ(2) = -409.4 кНм2
- EJ×v(2) = -1598 кНм3
EJ×φ(2.5) = -132.3 кНм2
- EJ×v(2.5) = -1732 кНм3
- EJ×φ(3) = 112.8 кНм2
- EJ×v(3) = -1736 кНм3
- EJ×φ(3.5) = 324 кНм2
- EJ×v(3.5) = -1625 кНм3
- EJ×φ(4) = 499.3 кНм2
- EJ×v(4) = -1418 кНм3
- На участке CD
- EJ×φ(4) = 499.3 кНм2
- EJ×v(4) = -1418 кНм3
EJ×φ(4.25) = 572.9 кНм2
- EJ×v(4.25) = -1284 кНм3
- EJ×φ(4.5) = 637 кНм2
- EJ×v(4.5) = -1132 кНм3
EJ×φ(4.75) = 691.6 кНм2
EJ×v(4.75) = -966.1 кНм3
- EJ×φ(5) = 736.8 кНм2
- EJ×v(5) = -787.3 кНм3
- На участке DE
- EJ×φ(5) = 736.8 кНм2
- EJ×v(5) = -787.3 кНм3
- EJ×φ(5.25) = 770 кНм2
EJ×v(5.25) = -598.8 кНм3
EJ×φ(5.5) = 793.7 кНм2
EJ×v(5.5) = -403.1 кНм3
EJ×φ(5.75) = 807.9 кНм2
EJ×v(5.75) = -202.8 кНм3
EJ×φ(6) = 812.6 кНм2
EJ×v(6) = 0 кНм3
Не получается решить задачу? Есть вопросы? Нужна помощь? Обратитесь к авторам сайта через ВКонтакте Telegram: sopromat_xyz WhatsApp: +380936422175
Источник: https://sopromat.xyz/projects/beams?id=274130
Расчёт металлической балки онлайн (калькулятор)
1. Сбор нагрузок
Перед началом расчета стальной балки необходимо собрать нагрузку, действующая на металлическую балку. В зависимости от продолжительности действия нагрузки разделяют на постоянные и временные.
К постоянным нагрузкам относятся:
- собственный вес металлической балки;
- собственный вес перекрытия и т.д.;
К временным нагрузкам относятся:
- длительная нагрузка (полезная нагрузка, принимается в зависимости от назначения здания);
- кратковременная нагрузка (снеговая нагрузка, принимается в зависимости от географического расположения здания);
- особая нагрузка (сейсмическая, взрывная и т.д. В рамках данного калькулятора не учитывается);
Нагрузки на балку разделяют на два типа: расчетные и нормативные. Расчетные нагрузки применяются для расчета балки на прочность и устойчивость (1 предельное состояние).
Нормативные нагрузки устанавливаются нормами и применяется для расчета балки на прогиб (2 предельное состояние). Расчетные нагрузки определяют умножением нормативной нагрузки на коэффициент нагрузки по надежности.
В рамках данного калькулятора расчетная нагрузка применяется при определении прогиба балки в запас.
Общий расчет металлоконструкций можно почитать нашем сайте.
Нагрузки можно собрать на нашем сайте.
После того как собрали поверхностную нагрузку на перекрытие, измеряемой в кг/м2, необходимо посчитать сколько из этой поверхностной нагрузки на себя берет балка. Для этого надо поверхностную нагрузку умножить на шаг балок(так называемая грузовая полоса).
Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 500кг/м2, а шаг балок 2,5м. Тогда распределенная нагрузка на металлическую балку будет: Qраспр.= 500кг/м2 * 2,5м = 1250кг/м. Эта нагрузка вносится в калькулятор
2. Построение эпюр
Далее производится построение эпюры моментов, поперечной силы. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.
3. Расчет по прочности и прогибу
После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и из таблицы сортамента выбрать подходящий металлопрофиль.
Вертикальный предельный прогиб fult принимается по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия). Пункт2.а в зависимости от пролета. Например предельный прогиб fult=L/200 при пролете L=6м.
означает, что калькулятор подберет сечение прокатного профиля (двутавра, швеллера или двух швеллеров в коробку), предельный прогиб которого не будет превышать fult=6м/200=0,03м=30мм.
Для подбора металлопрофиля по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента подбирают подходящий металлопрофиль.
4. Подбор металлической балки из таблицы сортамента
Из двух результатов подбора (1 и 2 предельное состояние) выбирается металлопрофиль с большим номером сечения.
Источник: http://3d-konstruktiv.com/raschet-metalicheskoy-balki-online
Расчет балок на прочность онлайн
Расчет простой балки на прочность и жесткость
Инструкция к программе
Программа написана на языке PHP и предназначена для использования студентами строительных вузов при выполнении расчетно-графической работы (РГР) «Расчет балки на прочность и жесткость». Все расчеты выполняются Online, что освобождает студентов от необходимости посещать компьютерный класс.
При использовании программы студентами машиностроительных вузов следует заменить следующие термины: нормативное сопротивление Rn – на предельное напряжение, расчетное сопротивление R – на допускаемое напряжение, коэффициент надежности по материалу γ – на коэффициент запаса прочности, коэффициент надежности по нагрузке γf положить равным единице. Кроме того, сечение стальной балки подбирается по предельному состоянию всего сечения, а в машиностроении основным методом расчета на прочность является метод допускаемых напряжений.
Подробно методика расчета, реализованная в данной программе, изложена в следующих методических указаниях: «Расчет балки на прочность» Скачать
«Расчет балки на жесткость» Скачать
Порядок выполнения расчетов
Расчет начинаем с пункта «Исходные данные». Начало отсчета располагается на левом конце балки, ось x направлена вправо, ось y – вниз.
Сосредоточенные силы, включая опорные реакции, и распределенные нагрузки считаются положительными, если направлены вниз. Момент пары сил считается положительным, если направлен по часовой стрелке. Вводить следует значения нормативных нагрузок.
Так как программа используется в учебных целях, то число нагрузок любого типа должно быть не более 10!
Пункты главного меню, выделенные серым цветом, неактивны на соответствующем этапе вычислений. При нажатии на них откравается окно с указанием того, что нужно сделать для продолжения расчетов.
Исходные данные расположены в следующем порядке: — тип балки: 0 – шарнирно опертая, 1 – с заделкой; — длина балки; — для шарнирно опертой балки координаты опор; — для балки с заделкой указание на то, левый или правый конец защемлен; — коэффициент надежности по нагрузке (используется при расчете балки на прочность); — число сосредоточенных сил; — число пар сил; — число распределенных нагрузок; — для каждой сосредоточенной силы – величина и координата точки приложения; — для каждой пары сил – величина и координата сечения, в котором она действует; — для каждой распределенной нагрузки – интенсивность нагрузки в начале и в конце участка, на котором она действует, и координаты концов этого участка.
В качестве разделителя целой и дробной частей вещественного числа используется точка.
Линия по переработке автошин
Распределенные нагрузки предполагаются распределенными по линейному закону. Если какой-либо тип нагрузок отсутствует, то следует положить число этих нагрузок равным нулю. После ввода исходных данных нажимаем на ссылку «Продолжить расчет» и переходим на вкладку «Эпюры Q(x) и M(x)» для нахождения опорных реакций, построения эпюр поперечной силы и изгибающего момента и нахождения Mmax.
Далее можно выполнить подбор сечения двутавровой балки (нормативное сопротивление и коэффициент надежности по материалу вводятся по дополнительному запросу) и выполнить расчет прочности в заданном сечении.
Затем перейти к нахождению прогибов и углов поворота сечений. При этом следует задать значение модуля упругости.
Величина момента инерции сечения либо задается (в этом случае подбор сечения можно опустить), либо используется момент инерции подобранного ранее двутавра.
Источник: https://crast.ru/instrumenty/raschet-balok-na-prochnost-onlajn
Онлайн калькулятор расчет балки на прочность
- Получить объект с достаточным запасом прочности под воздействием собственного веса, а также ветровых и снеговых нагрузок.
- Подобрать минимально допустимый для строения профиль с целью минимизировать расходы на материалы.
Для достижения этой цели необходимо воспользоваться нашим онлайн калькулятором и рассчитать балку из трубы на изгиб. Это в случае, если деталь закреплена с одной стороны (консольная).
Если же закреплены оба конца, понадобится рассчитать балку на прогиб.
При этом необходимо учитывать следующие обстоятельства:
- Размеры и сечение: (профильная или круглая). Для балки из профильной прямоугольной трубы расчет производится с учетом направления воздействия. При расчете балок из квадратной трубы этот фактор одинаков для любого направления воздействия.
- Прочностные характеристики материала с учетом толщины стенок и марки материала. Это особенно актуально при использовании балок из круглой трубы, расчет которой в значительной степени зависит от указанных характеристик ввиду многообразия применяемых материалов.
Виды вероятных нагрузок
Как можно классифицировать нагрузки на балку? В соответствии с СП 20.13330.2011 «Нагрузки и воздействия» моменты нагружения конструкции можно распределить по следующим признакам:
- постоянные – давление и вес которых не изменяются с течением времени, это такие, как собственный вес конструкции;
- временные длительные, учитывающие вес дополнительных конструкций сооружения, включая оборудование, мебель и прочее;
- кратковременные поперечные, зависящие от внешних условий эксплуатации – нагрузки от ветра, снега или дождя, для определения которых производится собственный расчет, зависящий от района расположения объекта. Такие нагружения в экстремальных условиях создают условия, при которых возможно прогибание балки.
- особые условия воздействия, к которым можно отнести воздействие от удара автомобиля во время парковки, в результате которого опора может прогибаться;
- сейсмические – для местностей с определенной сейсмической активностью.
Прочностью перекрытия определяется уровень безопасности проживания на загородном участке или в деревенском доме.
Степень нагружения конструкций можно подбирать по таблицам, при этом учитываются:
- величина момента инерции, обозначенная в стандартах;
- длина пролета;
- величина нагрузки;
- модуль Юнга (справочные данные).
В таблицах приводятся готовые данные, рассчитанные по специальной формуле например для круглых, квадратных и прямоугольных профилей.
Все прочностные расчеты несущих конструкций по определению сложны в исполнении и требуют специальной инженерной подготовки в области сопротивления материалов. Поэтому лучше воспользоваться специальным онлайн-калькулятором.
Чтобы рассчитать нагрузки достаточно ввести исходные данные в таблицу и на выходе можно получить точный результат быстро и без особых затруднений.
Балочная ферма, подсчет которой произведен таким образом, будет надежной конструкцией на долгое время. При правильном расчете предельная жесткость перекрытия гарантирована.
Источник: https://stroyka.ahuman.ru/onlajn-kalkuljator-raschet-balki-na-prochnost/