- 1. Работа выхода электронов из металла.
- 3. Контактная разность потенциалов
- 4. Закон Вольта
- 5. Термо-ЭДС
- 6. Эффект Пельтье,1834 г
- 7. Эффект Томсона.
- Глава 4. Контактные явления
- Контактные явления, контактная разность потенциалов
- Контактная разность потенциалов
- Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
- Таблица работа выхода электронов из простых веществ
- Таблица работа выхода электронов из неорганических соединений
- Работа выхода | это… Что такое Работа выхода?
- Работа выхода в фотоэффекте
- Измерение работы выхода
- Работа выхода электрона из различных металлов
- Литература
1. Работа выхода электронов из металла.
Электроны проводимости в кристалле находятся в потенциальной яме. Выход из нее требует совершения работы по преодолению силы, действующей на электрон со стороны кристалла. Найдем эту силу.
Обладая энергией теплового движения, электроны могут выскакивать из кристалла на расстояние в несколько периодов. Вышедший из кристалла и находящийся у его поверхности на расстоянии х электрон индуцирует в металле заряд е+ (рис.97).
Этот наведенный заряд действует на вышедший электрон так, как если бы он был сосредоточен под поверхностью металла на глубине х в точке, симметричной той, в которой находится электрон (см. Эл-во §5). Индуцированный заряд е+ называется электрическим изображением заряда е-.
Оба точечные заряда притягиваются друг к другу с силой Кулона . (14.1)
Но это и есть сила притяжения металлом вышедшего из него электрона. Под действием этой силы электрон втягивается обратно в металл. Чтобы удалить электрон из металла, надо совершить работу по преодолению этой силы, перемещая электроны на бесконечность из точки, расположенной на расстоянии х0 от поверхности металла. В качестве х0 можно взять межатомное расстояние.
На рис.98 показана зависимость потенциальной энергии электрона от расстояния х до атомной плоскости – стенки металла.
Энергетическое расстояние еj от уровня Ферми до нулевого уровня называют термодинамической работой выхода электрона, величину j – потенциалом выхода. Уровень Ес обозначает дно зоны проводимости, где Е = 0.
У металлов работа выхода еj заключена в пределах 1,8 ¸ 5,3 эВ. Меньше всего она у щелочных металлов, больше – у золота, серебра, платины (табл. 14.1).
| Таблица 14.1 | |||
| Металл | еj, эВ | Металл | еj, эВ |
| Литий Li | 2,38 | Платина Pt | 5,32 |
| Натрий Na | 2,35 | Ванадий V | 4,58 |
| Калий К | 2,22 | Вольфрам W | 4,54 |
| Рубидий Rb | 2,16 | Золото Au | 4,30 |
| Цезий Cs | 1,18 | Серебро Ag | 4,30 |
Большое влияние на работу выхода оказывают мономолекулярные адсорбированные слои. Например, слой атомов цезия Cs на вольфраме W (рис.99). Цезий щелочной металл. Его внешний, валентный электрон связан с ядром значительно слабее, чем валентные электроны в вольфраме. Поэтому атомы цезия отдают вольфраму свои валентные электроны и превращаются в положительные ионы.
Между этими ионами и их электрическими изображениями в вольфраме возникает сила притяжения, удерживающая ионы цезия на поверхности вольфрама. Поле этого двойного электрического слоя помогает выходу электронов из вольфрама. По этому в присутствии слоя цезия работа выхода электрона из вольфрама уменьшается с 4,54 эВ до 1,38 эВ.
Подобно цезию действуют одноатомные слои бария Ba, церия Cе, тория Th и др.
С повышением температуры металла поверхность Ферми разрыхляется, энергия электронов увеличивается, и они поднимаются на более высокие уровни (рис.100). Соответственно уменьшается работа выхода электронов. Поэтому концентрация вылетевших из кристалла электронов в пристеночном слое растет. Процесс испускания электронов нагретым металлом называется термоэлектронной эмиссией.
Формально термоэлектронная эмиссия есть всегда, когда Т > 0 К. Но заметной она становится при температурах Т > 800 К.
Облако термоэлектронов находится в динамическом равновесии. Число вылетевших из металла электронов в каждый промежуток времени примерно равно числу электронов, втянутых в металл. Поэтому суммарный ток эмиссии равен нулю.
На основе термоэлектронной эмиссии построен ламповый вакуумный диод (рис.101). Здесь К – катод, обычно нагреваемая вольфрамовая спираль, А – анод, холодная металлическая пластина обычно цилиндрической формы. По оси этого цилиндра натягивается спираль катода. Оба электрода помещаются в стеклянный сосуд с высоким вакуумом.
Если между катодом и анодом создавать электрическое поле с напряжением U, как показано на рис.101, то термоэлектроны под действием этого поля будут перемещаться от катода к аноду. Возникает электрический ток в вакууме. Вольтамперная характеристика вакуумного диода показана на рис.102.
С повышением анодного напряжения U ток I через анод растет почти пропорционально U. Но при достижении некоторого значенья Iнас перестает увеличиваться. Это предельное значение Iнас называют ток насыщением.
Он возникает тогда, когда все электроны, вылетевшие из нагретого катода, захватываются полем и переносятся к аноду.
С повышением температуры катода ток насыщения увеличивается. Разделив ток насыщения на поверхность S катода, получаем плотность тока насыщения jнас = iнасçS. В 1901г.
Оуэн Ричардсон, исходя из классических представлений, теоретически нашел зависимость плотности тока насыщения от температуры поверхности катода. Уточненная Дешманом в 1923г. с учетом квантовых представлений, зависимость jнас(Т) имеет вид: . Формула Ричардсона-Дэшмана (14.2)
Здесь еj – работа выхода, А – константа, имеющая разное значение у разных металлов и колеблющаяся около теоретического значения А= 1,2·106 Аç(м2К2).
3. Контактная разность потенциалов
Рассмотрим процессы, происходящие при контакте двух разных металлов. Допустим, до электрического контакта металл 1 (на рис.103 слева) имеет работу выхода еj1, а работа выхода металла 2 больше, j2 > j1.
Приведем металлы в состояние электрического контакта, то есть сблизим их до такого расстояния, при котором возможен эффективный обмен электронами. Поскольку работа выхода электронов из металла 2 больше, то уровень Ферми в металле 2 ниже, чем в металле 1. В результате электроны проводимости с уровня Ферми металла 1 начинают переходить на уровень Ферми металла 2.
В результате такого перехода электронов металл 2 заряжается отрицательно, энергия электронов и, соответственно, уровень Ферми в нем повышаются. Металл 1 заряжается положительно, энергия электронов и уровень Ферми в нем понижаются. Между металлами возникает контактная разность потенциалов j12.
Суммарное перетекание зарядов прекратится, когда уровни Ферми сравняются, а разность потенциалов между проводниками будет равна разности потенциалов выхода, j12 = j2 — j1, и встречные потоки электронов сравняются n21=-n12 (рис.103 справа). Контактная разность потенциалов между проводниками создает для электронов, переходящих в проводник с большей работой выхода, потенциальный барьер высотой еj12.
Оценим количество электронов, перетекающих из одного металла в другой при возникновении контактной разности потенциалов j12.
Будем считать, что между контактирующими металлами остается зазор шириной d, а заряды концентрируются на контактирующих поверхностях.
Тогда заряд Q на каждой из поверхностей, необходимый для создания напряжения j12, найдется из формулы плоского конденсатора, . (14.3)
Как видно из таблицы 14.1, контактная разность потенциалов В. Расстояние d между металлами не может быть меньше параметра решетки а » 0,3 нм. Полагая j12 =1 В и d = 0,3 нм, получаем максимальную плотность заряда на контактирующих поверхностях.
.
Разделив на заряд электрона получаем, что на 1 м2 поверхности приходится 2·1017 электронов.
Если диаметр атомов взять равным постоянной решетки а = 0,3 нм, то на 1 м2 поверхности в одноатомном слое металла размещается атомов.
Если атомы металла содержат по одному валентному электрону, то для создания контактной разности потенциалов 1 В потребовалось всего лишь (2×1017ç1019)´100% = 2% электронов проводимости одноатомного поверхностного слоя.
4. Закон Вольта
Контактную разность потенциалов открыл в девяностых годах XVIII века итальянец Александр Вольта.
В серии экспериментов 1792–1794 годов он установил, что в цепочке из ряда последовательно соединенных металлов контактная разность потенциалов зависит лишь от крайних металлов. Этот опытный факт называется законом Вольта.
Действительно, пусть имеется цепочка из металлов 1,2,3,4 (рис.104). Работа выхода металлов еj1, еj2, еj3, еj4. На границе каждой пары возникает контактная разность:
(14.4)
Просуммировав левые и правые части, получаем: . (14.5)
Сумма всех контактных ЭДС (левой части равенства) равна контактной ЭДС крайних металлов в цепочке (правая часть равенства). Если концы цепи замкнуть, то независимо от количества звенев сумма контактных разностей потенциалов равна нулю. Тока в цепи нет.
5. Термо-ЭДС
Сумма контактных разностей потенциалов в замкнутой цепи равна нулю лишь при условии, что температуры всех контактов одинаковы. В 1821 г. Томас Зеебек, сжимая концы висмутовой и медной пластинок теплыми пальцами обнаружил, что если цепь замкнута, то в ней протекает ток.
Это явление возникновения ЭДС в цепи из разных металлов при перепаде температур между спаями называют эффектом Зеебека или термоэлектричеством.
В рамках классической электронной теории можно дать простое толкование явлению Зеебека и получить зависимость термо-ЭДС от перепада температур.
Пусть имеется замкнутая цепь из двух металлов 1 и 2 со спаями A и B (рис.105). Полагаем, что электроны проводимости на верхних уровнях зоны проводимости распределяются в силовом поле решетки по закону Больцмана.
(14.6), (14.7)
Здесь n01 и n02 – концентрация электронов проводимости на уровнях Ферми. В силу полной заполняемости этих уровней будем полагать n01 = n02; U1 и U2 – потенциальная энергия электронов в металлах 1 и 2. Она может изменяться от нуля на уровне Ферми до еj (работа выхода) на нулевом уровне. Разделим первое уравнение на второе.
. (14.8)
Разделив разность U1 –U2 на заряд электрона е, получаем концентрационную разность потенциалов между металлами 1 и 2. . (14.9)
Если температуры спаев ТА и ТB одинаковы, то концентрационная ЭДС в замкнутой цепи, так же, как контактная разность потенциалов, равна нулю. Тока в цепи нет. Если же температуры спаев разные, ТА ¹ ТB, то в цепи возникает термо-ЭДС (рис.106). Концентрационные перепады потенциалов в контактах А и B разные.
. (14.10)
Концентрация свободных электронов слабо зависит от температуры. Поэтому можно полагать, что n1A = n1В= n1, n2A = n2В = n2. ЭДС, возникающая в цепи, равна . (14.11)
| Таблица 14.2 | |
| Пара | а, |
| Висмут – Платина | –65,0 |
| Железо – Платина | +16,0 |
| Медь – Платина | +7,4 |
| Никель – Платина | –16,4 |
| Сурьма – Платина | +47,0 |
| Константан – Платина | –34,4 |
Учитывая грубость классических приближений, обычно выделяют лишь температурную зависимость, которая хорошо подтверждается опытом при малых перепадах температур, . (14.12)
Коэффициент а называют дифференциальной термо-ЭДС пары металлов. В таблице 14.2 приведены значения а для наиболее употребительных металлов в паре с платиной. Чтобы определить величину а пары металлов без платины, надо найти разность значений а в таблице. Например, для пары Bi – Sb, а = -65,0 — 47,0 = -112,0 мкВçК. Для пары медь – константан а = +7,4 — (-34,4) = 48,8 мкВçК.
Термо-ЭДС, возникающая в цепи из разных металлов, широко применяется для измерения температур в диапазоне от 0 К до » 1000°С. Соответствующее устройство из двух разных металлов называется термопарой.
Один спай термопары поддерживается при постоянной температуре, например при 0оС в сосуде с тающим льдом, другой помещают в ту среду, температуру которой хотят измерить.
О величине температуры можно судить как по величине термотока, измеряемого гальванометром, так и более точно по величине термо-ЭДС, измеряемой методом компенсации. С помощью термопар можно измерять температуру с точностью до сотых долей градуса.
6. Эффект Пельтье,1834 г
Он обратен эффекту Зеебека и состоит в том, что при пропускании тока по цепи из разных металлов один контакт у металла нагревается, другой охлаждается.
Пусть в цепи из двух разных металлов действует источник тока – батарея Б. В результате в цепи идет постоянный ток I (рис.107).
Проходя спай B, электроны, идущие по цепи на рисунке против часовой стрелки, дополнительно ускоряются полем контактного потенциала.
Их скорость дрейфа увеличивается, поэтому при столкновении с узлами электроны передают им большую, по сравнению со средней, энергию. Спай В нагревается больше, чем рядом расположенные участки проводников.
В спае А электроны тормозятся контактным полем, их скорость дрейфа уменьшается, поэтому спай А нагревается меньше, чем рядом расположенные участки проводов.
Кроме того, для установления равновесия этих электронов с электронным газом им необходимо приобрести еще энергию. Эту энергию они черпают из решетки.
В результате спай А охлаждается больше, чем нагревается. В итоге теплота в спае А поглощается.
Выделяющаяся или поглощающаяся теплота Пельтье QП в контакте пропорциональна заряду It, прошедшему через контакт. . (14.13)
Здесь П – коэффициент Пельтье связан с дифференциальной термо-ЭДС соотношением: П = аDT.(14.14)
Где DТ – разность температур между контактами.
Эффект Пельтье позволяет создавать малогабаритные холодильные устройства. Их особенность в том, что изменяя направление тока в цепи, можно один и тот же контакт заставить как поглощать тепло (холодильник), так и выделять его (нагреватель).
7. Эффект Томсона.
В 1853 – 54 г.г. Рудольф Клаузиус и Уильям Томсон независимо друг от друга применили к явлениям термоэлектричества принципы термодинамики.
В процессе построения термодинамической теории термоэлектричества Томсон установил, что неравномерно нагретый проводник должен вести себя как система находящихся в контакте физически разнородных участков.
На этом основании Томсон пришёл к заключению и подтвердил его экспериментально, что в однородном неравномерно нагретом проводнике должно выделяться или поглощаться тепло Пельтье (тепло Томсона). Само явление назвали эффектом Томсона.
Принципиальная схема экспериментальной установки изображена на рис.108
Концы двух одинаковых проводящих стержней помещены в два термостата с разными температурами Т1 и Т2. Допустим, Т1 > Т2. Тогда градиент температуры в верхнем стержне направлен по току I, а в нижнем – против тока. В результате в одном стержне выделяется тепло Томсона (его температура выше), а в другом – поглощается.
Знак эффекта у разных проводников разный. В висмуте и цинке, например, тепло выделяется, если поток тепла и электрический ток совпадают по направлению (на рисунке нижний проводник). А в Fe, Pt, Sb при тех же условиях тепло поглощается. С изменением направления тока знак эффекта во всех проводниках меняется.
Тепло Томсона Q, выделяющееся в проводнике, пропорционально перепаду температур ΔТ, току I, протекающему по проводнику, и времени t Q = σΔTIt.
Здесь σ – коэффициент Томсона. Он зависит от материала провода и от его температуры. Коэффициент σ невелик. У металлов он порядка 10–5 ВçК. За положительное направление тока принимают направление градиента температур, то есть направление от холодного конца проводника к горячему. Если тепло при этих условиях выделяется (проводник нагревается), эффект Томсона считается положительным.
Количественно эффект Томсона исследовал в 1867 г. Франсуа Леру. В установке, собранной по схеме рис. 108, к поверхности стержней он присоединял спаи термопар. Пока тока через стержни не было, термоЭДС в цепи термопар была равна нулю. При включении тока через стержни появлялась термоЭДС, величина и знак которой позволяли определить коэффициент Томсона σ.
8. Закон Джоуля – Ленца в замкнутой цепи всегда выполняется. Суммарный эффект Пельтье и Томсона в замкнутой цепи равен нулю, поскольку наряду с участками цепи, где тепло Пельтье и Томсона выделяется, всегда есть участки, где такое же тепло поглощается.
Глава 4. Контактные явления
Современная терраса: материалы и оборудование
Концентрация свободных электронов в металлах очень велика (порядка 1023 см-3). Находясь в постоянном хаотическом движении, они беспрерывно подходят к поверхности. Однако если металл не нагрет, то выхода электронов за пределы образца практически не наблюдается. Объясняется это следующим образом.
Внутри металла каждый свободный электрон при перемещении в межузельном пространстве взаимодействует со всеми окружающими его электронами, а также с положительно заряженными атомными остатками, создающими кристаллическую решетку.
Благодаря равномерному распределению заряженных частиц в объеме кристалла равнодействующая всех сил, действующих на каждый электрон, оказывается в среднем практически равной нулю.
При подходе же электрона к поверхности, а тем более при его выходе из кристалла равномерность распределения заряженных частиц вокруг него нарушается, и это приводит к возникновению сил, препятствующих выходу электрона за пределы кристалла.
Можно рассмотреть две причины, затрудняющие выход электронов: образование у границы металла двойного электрического слоя и возникновение при выходе электрона так называемой силы зеркального отображения.
Двойной электрический слой. Даже при абсолютном нуле температуры свободные электроны в металле обладают достаточно большой кинетической энергией. Однако притяжение к узлам кристаллической решетки, заряженным положительно, не дает электрону покинуть металл совсем.
Благодаря этому металл оказывается окруженным электронным облаком (рис. 43).
Образующийся у поверхности двойной электрический слой можно рассматривать как плоский конденсатор, одной обкладкой которого являются приповерхностные положительные ионы, оставшиеся нескомпенсированными после ухода электронов, а другой — представленное в виде тонкого слоя электронное облако. Очевидно, что напряженность поля внутри такого конденсатора может считаться постоянной. Если а — расстояние между указанными обкладками, то сила F1, препятствующая прохождению электрона, вычисляется по формуле
а энергия W1, которую необходимо затратить электрону на преодоление двойного слоя, по формуле
Рис. 43
Сила зеркального отображения. Преодолев двойной слой, электрон тем не менее еще не освобождается от воздействия со стороны металла.
Дальнейшему удалению его препятствует сила зеркального отображения: на электрон, находящийся на расстоянии х от поверхности металла, действует со стороны этой поверхности сила, которая может быть определена как сила взаимодействия данного электрона с частицей, имеющей положительный заряд, равный модулю заряда электрона, и находящейся в глубине металлического тела на расстоянии х от поверхности (рис. 44). По закону Кулона сила зеркального отображения, действующая на электрон в вакууме, выражается формулой
Рис. 44
Если предположить, что сила F1 при выходе за пределы двойного слоя непрерывно переходит в силу F2 то общий график силы, действующей на электрон по мере его удаления от поверхности металла, можно представить кривой, приведенной на рисунке 45. Энергия же, необходимая для преодоления силы зеркального отображения, равна
Рис. 45
Полная работа выхода. Электрон, покидающий металл, должен преодолеть своеобразный потенциальный барьер, показанный на рисунке 46. Часть этого барьера (на участке от 0 до а) создана силами двойного слоя, а другая часть (на участке от а до ∞) — силами зеркального отображения.
Общая же высота W0 потенциального барьера равна той работе, которую должен совершить электрон на пути от поверхности металла до полного отделения от металла. Величина W0 называется полной работой выхода.
Экспериментально определенные значения полной работы выхода для различных металлов лежат в интервале от 3 до 20 эВ.
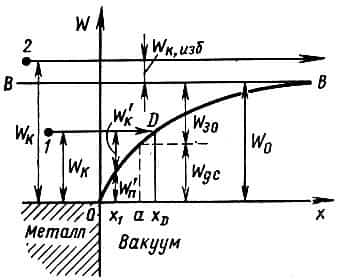 Рис. 46
Рис. 46
Ход потенциального барьера можно рассматривать как кривую, отражающую изменение потенциальной энергии электрона по мере его удаления от поверхности металла.
Действительно, электрон, находящийся внутри металла и обладающий некоторой кинетической энергией Wк (рассмотрим, например, электрон, обозначенный цифрой 1), может перемещаться в любом направлении без изменения энергии.
Однако если он переходит границу металла — вакуум, то кинетическая энергия электрона в соответствии с законом сохранения энергии начинает превращаться в потенциальную. Так, если электрон отошел от границы на расстояние x1, то часть его кинетической энергии перейдет в потенциальную W'п.
Поскольку, дойдя до точки хи электрон сохранил еще часть кинетической энергии он может и дальше уходить от поверхности. Однако при удалении электрона на расстояние xD уже вся его кинетическая энергия преобразуется в потенциальную (точка D на кривой потенциальной энергии электрона). В этой точке скорость электрона оказывается равной нулю, после чего он возвращается обратно.
Для того чтобы электрон имел возможность окончательно покинуть металл, его кинетическая энергия должна быть не меньше высоты потенциального барьера W0. Такой возможностью обладает, например, электрон, обозначенный на рисунке цифрой 2.
Более того, поскольку начальная кинетическая энергия этого электрона превышает полную работу выхода, то, даже покинув металл, он сохранит некоторую скорость, соответствующую оставшейся неизрасходованной избыточной кинетической энергии:
Обычно за нулевой уровень отсчета энергии принимают не уровень неподвижного электрона в глубине металла, а уровень, соответствующий неподвижному электрону, находящемуся в вакууме достаточно далеко от поверхности металла и не испытывающему воздействия с его стороны. На рисунке 46 это уровень ВВ, к которому асимптотически приближается кривая потенциальной энергии электрона.
В этом случае объем металла является для электрона потенциальной ямой, глубина которой равна W0. При таком выборе нулевого уровня электроны, находящиеся внутри металла и расположенные ниже уровня ВВ, имеют отрицательную энергию.
О полной же работе выхода тогда говорят, что это работа, которая должна быть совершена электроном, первоначально находившимся на дне потенциальной ямы, при его выходе из этой ямы.
Контактные явления, контактная разность потенциалов
В металлах, согласно электронной теории проводимости, свободные электроны находятся в состоянии постоянного хаотичного теплового движения.
Однако при нормальных температурах они не покидают металл. У поверхности металла существует задерживающее электрическое поле.
Чтобы вылететь из металла электрон должен совершить работу по преодолению задерживающих сил. Эта работа называется работой выхода.
Работа выхода
- Работа выхода — работа, которую должен совершить электрон, чтобы выйти из металла.
- Формула для работы выхода:
- A=eU,
- где e — заряд электрона, U — разность потенциалов между точками в металле и за пределами задерживающего слоя.
- Работа выхода измеряется в электронвольтах.
- Электронвольт — внесистемная единица измерения, равная энергии, которую приобретает электрон при движении между двумя точками с разностью потенциалов в 1 Вольт.
Как у поверхности металла образуется задерживающее поле?
- Вследствие теплового движения электроны с поверхности металла могут отрываться и образуют над поверхностью электронное облако.
- На местах покинувших металл электронов образуются положительные ионы. По закону Кулона, они стремяться вернуть покинувшие металл электроны обратно.
В результате у поверхности металла образуется двойной электрический слой.
- В вакууме за пределами задерживающего слоя поле отсутствует, поэтому формула для работы выхода запишется в виде:
- A=eφ,
- где φ — потенциал выхода, равный потенциалу поля внутри металла.
Контактная разность потенциалов
Явление контактной разности потенциалов в 1797 году открыл Алессандро Вольта (1745 -1827).
Контактная разность потенциалов
Контактная разность потенциалов — разность потенциалов, которая возникает при контакте поверхностей двух разных металлов.
- Разность потенциалов, возникающая при контакте двух разных металлов, зависит от их химического состава и температуры.
- Если цепь составлена из нескольких разных проводников при одинаковой температуре, контактная разность потенциалов определяется только контактной разностью между крайними проводниками.
Причины возникновения контактной разности потенциалов:
- Разная работа выхода для разных металлов.
- Разная концентрация свободных электронов в разных металлах.
Схематически рассмотрим контакт двух металлов. Пусть у металла 1 работа выхода больше, чем у металла 2, и в металле 1 концентрация свободных электронов больше.
Между точками a и b, лежащими рядом с поверхностью, но не принадлежащими проводнику, возникает внешняя контактная разность потенциалов.
Электроны диффундируют из одного металла в другой, при этом из металла 1 в металл 2 уходит больше электронов, так как n1>n2. В результате металл 1 приобретает положительный, а металл 2 — отрицательный заряд. Возникшая разность потенциалов называется внутренней контактной разностью потенциалов.
Роман Адамчук
Преподаватель физики
речь и презентация к школьному проекту нужен проект на тему байкал в разные времена года зима весна класс
- Вид работы: Презентация (PPT, PPS)
- Выполнена: 28 марта 2022 г.
- Стоимость: 1 800 руб
Заказать такую же работу
Задачи во вложении
- Вид работы: Решение задач
- Выполнена: 23 января 2022 г.
- Стоимость: 2 200 руб
Заказать такую же работу
Универсальные меры предостарожности при работе с кровью и биологическими жидкостями
- Вид работы: Реферат
- Выполнена: 24 декабря 2021 г.
- Стоимость: 800 руб
Заказать такую же работу
Мне нужен реферат по теме ОКД норматив Ну процентов на орегинальности страницы Это кинология
- Вид работы: Реферат
- Выполнена: 30 ноября 2021 г.
- Стоимость: 1 000 руб
Заказать такую же работу
вопроса теории расчетно графическое задание
- Вид работы: Контрольная работа
- Выполнена: 14 октября 2021 г.
- Стоимость: 1 700 руб
Заказать такую же работу
Технология изготовления лекарственных средств
- Вид работы: Контрольная работа
- Выполнена: 11 июня 2021 г.
- Стоимость: 1 900 руб
Заказать такую же работу
Смотреть все работы по географии
Не получается написать работу самому?
Доверь это кандидату наук!
Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении.
Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла.
Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.
Потенциальная энергия электрона внутри металла постоянна и равна:
Wp = -eφ , где j – потенциал электрического поля внутри металла.
При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.
В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.
Aвых = eφ
Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.
Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.
Aвых = eφ' — EF
где φ' – среднее значение потенциала электрического поля внутри металла.
Таблица работа выхода электронов из простых веществ
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
| Вещество | Формула вещества | Работа выхода электронов (W, эВ) |
| серебро | Ag | 4,7 |
| алюминий | Al | 4,2 |
| мышьяк | As | 4,79 — 5,11 |
| золото | Au | 4,8 |
| бор | B | (4,60) |
| барий | Ba | 2,52 |
| бериллий | Be | 3,92 |
| висмут | Bi | 4,34 |
| углерод (графит) | C | 4,45 — 4,81 |
| кальций | Ca | 2,76 — 3,20 |
| кадмий | Cd | 4,04 |
| церий | Ce | 2,6 — 2,88 |
| кобальт | Co | 4,40 |
| хром | Cr | 4,60 |
| цезий | Cs | 1,94 |
| медь | Cu | 4,36 |
| железо | Fe | 4,40 — 4,71 |
| галлий | Ga | 3,96 — 4,16 |
| германий | Ge | 4,66 |
| гафний | Hf | (3,53) |
| ртуть | Hg | 4,52 |
| индий | In | (3,60 — 4,09) |
| иридий | Ir | (4,57) |
| калий | K | 2,25 |
| лантан | La | (3,3) |
| литий | Li | 2,49 |
| магний | Mg | 3,67 |
| марганец | Mn | 3,76 — 3,95 |
| молибден | Mo | 4,20 |
| натрий | Na | 2,28 |
| ниобий | Nb | 3,99 |
| неодим | Nd | (3,3) |
| никель | Ni | 4,91 — 5,01 |
| осмий | Os | (4,55) |
| свинец | Pb | 4,05 |
| палладий | Pd | (4,98) |
| празеодим | Pr | (2,7) |
| платина | Pt | 5,30 — 5,55 |
| рубидий | Rb | 2,13 |
| рений | Re | 4,98 |
| родий | Rh | 4,75 |
| рутений | Ru | (4,52) |
| сурьма | Sb | 4,08 — 4,56 |
| скандий | Sc | (3,2 — 3,33) |
| селен | Se | 4,86 |
| кремний | Si | 3,59 — 4,67 |
| самарий | Sm | (3,2) |
| олово (γ-форма) | Sn | 4,38 |
| олово (β-форма) | Sn | 4,50 |
| стронций | Sr | 2,74 |
| тантал | Ta | 4,13 |
| теллур | Te | 4,73 |
| торий | Th | 3,35 — 3,47 |
| титан | Ti | 4,14 — 4,50 |
| таллий | Tl | 3,68 — 4,05 |
| уран | U | 3,27 — 4,32 |
| ванадий | V | 3,77 — 4,44 |
| вольфрам | W | 4,54 |
| цинк | Zn | 4,22 — 4,27 |
| цирконий | Zr | 3,96 — 4,16 |
Таблица работа выхода электронов из неорганических соединений
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
| Вещество | Формула вещества | Работа выхода электронов (W, эВ) |
| бромистое серебро | AgBr | ~3,9 |
| хлористое серебро | AgCl | ~4,6 |
| иодистое серебро | AgI | ~4,0 |
| сульфид серебра | Ag2S | ~3,8 |
| триоксид бора | B2O3 | 4,7 |
| оксид бария | BaO | 1,0 — 1,6 |
| барий вольфрамовокислый | BaWO4 | 2,27 |
| окись бериллия | BeO | 3,8 — 4,7 |
| окись кальция | CaO | 1,8 — 2,4 |
| ортовольфрамат кальция | Ca3WO6 | 2,13 |
| борид хрома | CrB2 | 3,36 |
| окись цезия | Cs2O | 1,0 — 1,17 |
| окись меди | CuO | 4,35 — 5,34 |
| закись меди | Cu2O | 5,15 |
| окись железа | FeO | 3,85 |
| вода | H2O | 6,1 |
| карбид гафния | HfC | 2,04 |
| оксид магния | MgO | 3,1 — 4,4 |
| диборид марганца | MnB2 | 4,14 |
| диборид молибдена | MoB2 | 3,38 |
| триоксид молибдена | MoO3 | 4,25 |
| силицид молибдена | MoSi2 | 5,0 — 6,0 |
| хлористый натрий | NaCl | 4,2 |
| борид ниобия | NbB2 | 3,65 |
| карбид ниобия | NbC | 2,24 |
| окись никеля | NiO | 5,55 |
| борид скандия | ScB2 | 2,3 — 2,9 |
| кремнезём | SiO2 | 5,0 |
| окись стронция | SrO | 2,0 — 2,6 |
| карбид тантала | TaC | 3,05 — 3,14 |
| пентаоксид тантала | Ta2O5 | 4,65 |
| дикарбид тория | ThC2 | 3,5 |
| оксид тория | ThO2 | 2,54 — 2,67 |
| сульфид титана | TiS | 3,4 |
| диборид титана | TiB2 | 3,88 — 3,95 |
| карбид титана | TiC | 2,35 — 3,35 |
| нитрид титана | TiN | 2,92 |
| окись титана | TiO | 2,96 — 3,1 |
| двуокись титана | TiO2 | 4,7 |
| карбид урана | UC | 2,9 — 4,6 |
| диборид ванадия | VB2 | 3,88 — 3,95 |
| диборид вольфрама | WB2 | 2,62 |
| диоксид вольфрама | WO2 | 4,96 |
| дисилицид вольфрама | WSi2 | 5,0 — 6,0 |
| борид циркония | ZrB | 4,48 |
| диборид циркония | ZrB2 | 3,70 |
| карбид циркония | ZrC | 2,2 — 3,8 |
| нитрид циркония | ZrN | 2,92 |
_______________
Источник информации:
1. Landolt-Borstein's Zahlenwerte und Funktionen aus Phsik, Chemie, Astrunumie, Geophysik, Thechnik, 6-е издание., Берлин, т. I, ч.4, 1955; т. II, ч.6, разд. 1, 1959.
2. В.С. Фоменко. Эмиссионные свойства элементов и химических соединений. Изд. АН УСССР, Киев, 1961.
Работа выхода | это… Что такое Работа выхода?
Работа выхода — разница между минимальной энергией (обычно измеряемой в электрон-вольтах), которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, и энергией Ферми.
Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам (чтобы электрон прошёл весь двойной слой), но достаточно близко по сравнению с размерами макроскопических граней кристалла. При этом пренебрегают дополнительной работой, которую необходимо затратить на преодоление внешних полей, возникающих из-за перераспределения поверхностных зарядов. Таким образом, работа выхода для одного и того же вещества для различных кристаллографических ориентаций поверхности оказывается различной.
При удалении электрона на бесконечность его взаимодействие с зарядами, остающимися внутри твёрдого тела приводит к индуцированию макроскопических поверхностных зарядов (при рассмотрении полубесконечного образца в электростатике это называют «изображением заряда»).
При перемещении электрона в поле индуцированного заряда совершается дополнительная работа, которая определяется диэлектрической проницаемостью вещества, геометрией образца и свойствами других поверхностей.
За счет этого полная работа по перемещению электрона из любой точки образца в любую другую точку (в том числе и точку бесконечности) не зависит от пути перемещения, то есть от того, через какую поверхность был удален электрон. Поэтому в физике твёрдого тела эта работа не учитывается и не входит в работу выхода.
Работа выхода в фотоэффекте
Работа выхода в внешнем фотоэффекте — минимальная энергия, необходимая для удаления электрона из вещества под действием света
Измерение работы выхода
Единицами измерения работы выхода являются Джоуль (Дж) или электронвольт (эВ).
Работа выхода электрона из различных металлов
Единица измерения: эВ электронвольт
Источник: CRC Handbook of Chemistry and Physics version 2008, стр. 12-114.
Примечание: Работа выхода может зависеть от ориентации освещаемого кристалла. К примеру, Ag: 4.26, Ag(100): 4.64, Ag(110): 4.52, Ag(111): 4.74. Диапазоны изменения работы выхода для типичных кристаллографических направлений указаны в таблице.
| Ag: | 4.52 – 4.74 | Al: | 4.06 – 4.26 | As: | 3.75 | Au: | 5.1 – 5.47 | B: | ~4.45 |
| Ba: | 2.52 – 2.7 | Be: | 4.98 | Bi: | 4.31 | C: | ~5 | Ca: | 2.87 |
| Cd: | 4.08 | Ce: | 2.9 | Co: | 5 | Cr: | 4.5 | Cs: | 2.14 |
| Cu: | 4.53 – 5.10 | Eu: | 2.5 | Fe: | 4.67 – 4.81 | Ga: | 4.32 | Gd: | 2.90 |
| Hf: | 3.9 | Hg: | 4.475 | In: | 4.09 | Ir: | 5.00 – 5.67 | K: | 2.29 |
| La: | 3.5 | Li: | 2.93 | Lu: | ~3.3 | Mg: | 3.66 | Mn: | 4.1 |
| Mo: | 4.36 – 4.95 | Na: | 2.36 | Nb: | 3.95 – 4.87 | Nd: | 3.2 | Ni: | 5.04 – 5.35 |
| Os: | 5.93 | Pb: | 4.25 | Pd: | 5.22 – 5.6 | Pt: | 5.12 – 5.93 | Rb: | 2.261 |
| Re: | 4.72 | Rh: | 4.98 | Ru: | 4.71 | Sb: | 4.55 – 4.7 | Sc: | 3.5 |
| Se: | 5.9 | Si: | 4.60 – 4.85 | Sm: | 2.7 | Sn: | 4.42 | Sr: | ~2.59 |
| Ta: | 4.00 – 4.80 | Tb: | 3.00 | Te: | 4.95 | Th: | 3.4 | Ti: | 4.33 |
| Tl: | ~3.84 | U: | 3.63 – 3.90 | V: | 4.3 | W: | 4.32 – 5.22 | Y: | 3.1 |
| Yb: | 2.60 [1] | Zn: | 3.63 – 4.9 | Zr: | 4.05 |
Литература
- Solid State Physics, by Ashcroft and Mermin. Thomson Learning, Inc, 1976






