- Электронная проводимость металлов
- Электрический ток в металлах: подробное объяснение (формулы)
- Важно знать
- Классическая модель проводимости
- Выводы простым языком
- Электрическая проводимость различных веществ. Электронная проводимость металлов — Класс!ная физика
- Классическая электронная теория проводимости Друде-Лоренца
- Формула Друде
- Опыт Толмена и Стюарта
Как мы уже свами знаем, проводниками электрического тока могут быть вещества и в твёрдом, и в жидком, и в газообразном состояниях. Возникает закономерный вопрос: а какие частицы являются носителями электрического заряда в той или иной среде?
Мы уже с вами говорили о том, что в металлах носителями заряда являются свободные электроны. Наряду с металлами хорошими проводниками являются водные растворы или расплавы электролитов.
Заряженные частицы, обеспечивающие существование электрического тока в электролитах, образуются в результате электролитической диссоциации, то есть распада молекул растворяемого вещества на ионы под действием молекул растворителя.
Иными словами, в электролитах носителями заряда являются положительные и отрицательные ионы.
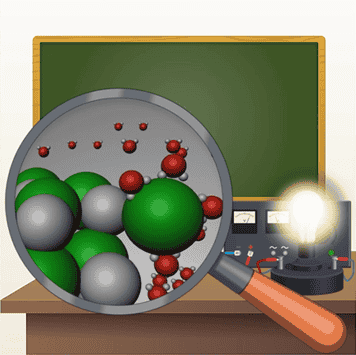
При определённых условиях газ также может являться хорошим проводником электрического тока. Носителями тока в этом случае выступают ионы и электроны.
А как вы думаете, возможен ли ток в вакууме? Для начала, давайте вспомним, что вакуум — это такое состояние газа в сосуде, при котором длина свободного пробега заряженных частиц превышает размеры сосуда. Проще говоря, вакуум — это идеальный изолятор, так как в нём отсутствуют свободные носители заряда.
Однако, если в сосуд с вакуумом поместить два электрода, один из которых — это подогреваемый спиралью катод, а второй — холодный анод, включённый в электрическую цепь, то электроны, вырвавшиеся с поверхности катоды, придут в упорядоченное движение и цепь замкнётся. Следовательно, носителями тока в вакууме являются электроны.
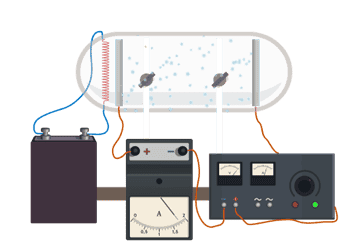
Также мы с вами говорили о том, что в природе существуют вещества, занимающие промежуточное положение между проводниками и диэлектриками — это полупроводники. В них носителями тока являются свободные электроны и дырки.
На сегодняшнем уроке мы с вами остановимся на подробном рассмотрении электронной проводимости металлов. Впервые она была экспериментально подтверждена немецким физиком-экспериментатором Эдуардом Рикке в 1901 году. Суть его опыта достаточно проста.
Он взял проводник, состоящий из трёх отполированных и плотно прижатых друг к другу двух медных и одного алюминиевого цилиндров известной массы, и в течение года пропускал по ним ток одного и того же направления. За это время через проводник прошёл чудовищный заряд — более чем 3,5 МКл.
После завершения опыта, Рикке опят взвесил цилиндры. Оказалось, что их массы остались неизменными. Более того, в местах контакта цилиндров также никаких изменений не произошло.
Этот, на первый взгляд, простой эксперимент послужил доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются общими для всех металлов, — электронами.
Убедительное доказательство электронной природы тока в металлах было получено в 1913 году в опытах русских физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американским физиком Ричардом Толменом и шотландским физиком Томасом Стюартом в 1916 году.
Идея обоих опытов такова. Берётся катушка с большим числом витков из тонкой проволоки, концы которой припаяны к двум металлическим дискам, изолированным друг от друга.
С помощью скользящих контактов катушка подключается к гальванометру. Затем её приводят в быстрое вращение (до полутора тысяч оборотов в минуту), и — резко останавливают.
При таком торможении катушки в цепи возникает кратковременный ток, обусловленный инерцией носителей заряда
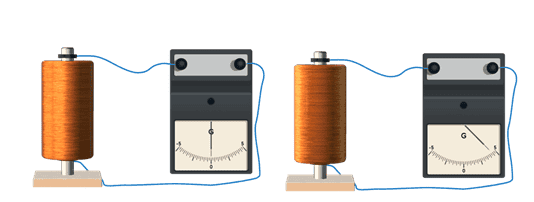
По направлению отклонения стрелки гальванометра было установлено, что электрический ток создают отрицательно заряженные частицы. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе:
Поэтому, измеряя заряд, проходящий через гальванометр за всё время существования тока в цепи, удалось определить отношение q0/m (то есть удельный заряд). Он оказался равным одной целой и восьми десятым на десять в одиннадцатой степени кулон на килограмм, что оказалось очень близко к величине удельного заряда электрона, найденному ранее из других опытов.:
Так было экспериментально доказано, что носителями свободных зарядов в металлах являются электроны.
В 1900—1904 гг., немецкий физик Пауль Друде и голландский физик Хендрик Лоренц разработали классическую электронную теорию проводимости металлов. Согласно этой теории любой металлический проводник можно рассматривать как физическую систему, состоящую из двух подсистем: свободных электронов с концентрацией ~1028 м–3 и положительно заряженных ионов, колеблющихся около положений равновесия.
Появление свободных электронов в металлическом кристалле упрощённо объяснить можно так. Электроны, находящиеся на внешних оболочках атомов, слабо связаны со своими ядрами.
А при образовании кристалла электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов.
В результате внешние электроны отрываются и могут двигаться по всему кристаллу в любом направлении, подобно частицам идеального газа. Эти электроны и называются свободными или электронами проводимости.
А совокупность свободных электронов в кристаллической решётке металла называют электронным газом.
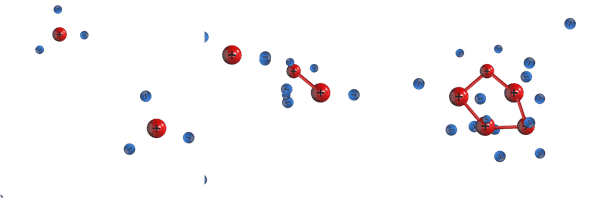
- Если к проводнику приложено внешнее электрическое поле, то на тепловое движение свободных электронов накладывается ещё направленное движение под действием сил электрического поля, что и порождает электрический ток.
- При этом считается, что движение электронов под действием сил электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими.
- Модель электронного газа даёт возможность теоретически объяснить природу сопротивления и вывести закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов.
В записанной формуле m0 — это масса электрона, а F — это постоянная сила, действующая на электрон со стороны электрического поля. Она равна произведению заряда электрона на напряжённость электрического в проводнике.
Тогда модуль средней скорости направленного движения электрона (она называется дрейфовой скоростью) линейно возрастает со временем:
Здесь t* — это усреднённое время между двумя последовательными столкновениями электрона с ионами кристаллической решётки.
Дрейфовая скорость электрона не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решётки электрон передаёт им кинетическую энергию, приобретённую в электрическом поле. Потом он опять ускоряется и процесс повторяется. В результате дрейфовая скорость электрона оказывается пропорциональной напряжённости электрического поля в проводнике.
Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля равен отношению напряжения между его концами к длине проводника:
- Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника: υ ~ U.
- Теперь давайте с вами вспомним, что сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:
Но, как мы показали с вами выше, дрейфовая скорость пропорциональна разности потенциалов на концах проводника. Следовательно, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.
Для закрепления материала решим с вами небольшую задачу. Как изменится дрейфовая скорость электронов в проводнике, если при неизменной площади поперечного сечения и разности потенциалов на его концах, увеличить длину этого проводника в три раза?
В заключении урока отметим, что построить удовлетворительную количественную теорию движения электронов в металле на основе законов классической механики невозможно.
А дело всё в том, что условия движения электронов в металле таковы, что для его описания классическая механика Ньютона неприменима. Этот факт подтверждается, например, зависимостью сопротивлений металлов от температуры.
Так в классической теории металлов, в которой движение электронов рассматривается на основе второго закона Ньютона, сопротивление проводника пропорционально квадратному корню из температуры.
А вот эксперименты говорят, что эта зависимость линейная. Однако об этом мы с вами поговорим в следующий раз.
Электронная проводимость металлов


Средняя оценка: 4.7
Всего получено оценок: 114.
Обновлено 7 Сентября, 2020
Средняя оценка: 4.7
Всего получено оценок: 114.
Обновлено 7 Сентября, 2020
В 10 классе известно, что вещество, являющееся проводником, должно содержать много высокоподвижных носителей электрического заряда. Наилучшими проводниками в нормальных условиях являются металлы. Кратко рассмотрим механизм электронной проводимости металлов.
Вещества, обладающие металлической проводимостью, как правило, имеют во внешней электронной оболочке малое количество электронов, которые относительно слабо связаны ядром и внутренними электронными оболочками. Это и определяет особенности металлической кристаллической решетки.
В кристалле металла ионы с внутренними электронными оболочками образуют узлы решетки, как и в любом другом кристалле.
А электронные облака внешних валентных электронов перекрывают друг друга так, что они оказываются общими не только для двух ионов (как это бывает в ковалентной связи), а сразу для нескольких ионов.
В результате электроны могут свободно перемещаться между всеми этими ионами, попадая в поле действия более далеких ионов, и перемещаясь уже между ними.
То есть, электроны в кристаллической решетке металла движутся не строго по орбитам между соседними атомами (как в ковалентном кристалле), а образуют своего рода «электронный газ», распределенный по всему кристаллу.
Рис. 1. строение металлической кристаллической решетки.
Такое строение кристаллической решетки приводит к тому, что электроны очень легко способны перемещаться под действием внешнего электрического поля. То есть, металлы, имеют много свободных легких электронов и обладают большой проводимостью.
Доказательством существования свободных электронов явились опыты, проведенные в 1916г Т. Стюартом и Р.Толменом (позже выяснилось, что такие же опыты ставились и ранее Л. Мандельштамом и Н.Папалекси, но результат их не был опубликован).
Идея этих опытов состоит в том, что если внутри металла существуют свободные электроны, то при движении кристаллической решетки с ускорением электроны должны «отставать» от ионов. В результате на разных концах кристалла концентрация электронов должна быть разной, и порождать разность потенциалов.
Для опыта использовалась катушка, к которой был подключен чувствительный телефонный капсюль. Когда катушка колебалась вокруг продольной оси, в ней возникала электроинерционная разность потенциалов, и капсюль издавал звук.
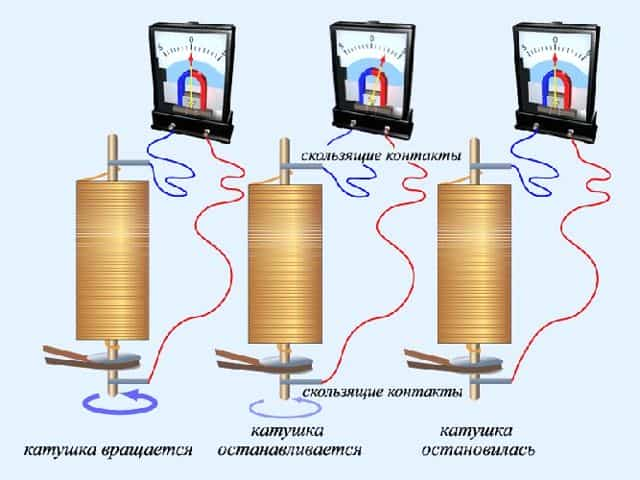 Рис. 2. Опыт Мандельштама и Папалекси.
Рис. 2. Опыт Мандельштама и Папалекси.
В 1900г П.Друде, основываясь на положениях молекулярно-кинетической теории, и рассматривая электроны в металле, как идеальный газ, создал классическую электронную теорию проводимости металлов. Первоначально эта теория не учитывала распределение скоростей электронов, учет этого распределения был выполнен в 1904г Х.Лоренцем.
Теория Друде-Лоренца смогла объяснить законы Ома, Джоуля-Ленца, механизм проводимости и зависимости сопротивления от температуры.
Однако, со временем стало появляться все больше данных, необъяснимых в рамках классичепской теории. В частности, имелись расхождения по температурному коэффициенту сопротивления, по значениям теплоемкости.
И уж совсем необъяснимым было явление сверхпродоимости, открытое в 1911г.
Все эти расхождения имеют квантовый характер, и поэтому объясняются в рамках более совершенной квантовой теории проводимости твердых тел (зонной теории проводимости).
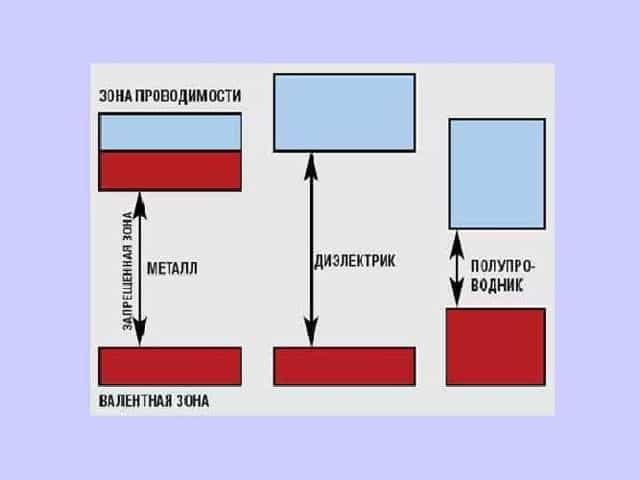 Рис. 3. Зонная теория проводимости.
Рис. 3. Зонная теория проводимости.
Высокая проводимость металлов обуславливается особенностями кристаллической решетки, в которой электронные облака соседних атомов сильно перекрываются друг с другом, поэтому электроны могут легко перемещаться между атомами, обеспечивая низкое электрическое сопротивление. Первоначально была разработана классическая теория проводимости Друде-Лоренца. В настоящее время она сменилась зонной теорией проводимости.
Чтобы попасть сюда — пройдите тест.
Средняя оценка: 4.7
Всего получено оценок: 114.
А какая ваша оценка?
Гость завершил
Тест «Евгений Онегин»с результатом 14/16
Гость завершил
Тест 3 том «Война и мир»с результатом 8/12
Гость завершил
Тест «Медный всадник»с результатом 10/11
Гость завершил
Тест Том 1 «Война и Мир»с результатом 9/12
Гость завершил
Тест «Биография Державина»с результатом 9/12
Гость завершил
Тест Дроби (5 класс)с результатом 3/10
Гость завершил
Тест «Маленький принц»с результатом 12/14
Гость завершил
Тест «Софья» (Горе от ума)с результатом 4/5
Гость завершил
Тест Том 1 «Война и Мир»с результатом 11/12
Гость завершил
Тест «Ревизор»с результатом 6/17
Гость завершил
Тест «Толстый и тонкий»с результатом 8/8
Не подошло? Напиши в х, чего не хватает!
Электрический ток в металлах: подробное объяснение (формулы)
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток – это упорядоченный поток носителей электрического заряда. Носители – это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в “облако” хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости.
В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда.
Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как “ро”). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр.
Удельное сопротивление – это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10-8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10-8 Ом .
В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10-8 |
| Медь | 1.72*10-8 |
| Алюминий | 2.82*10-8 |
| Вольфрам | 5.6*10-8 |
| Железо | 10*10-8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью “свободным”, поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).
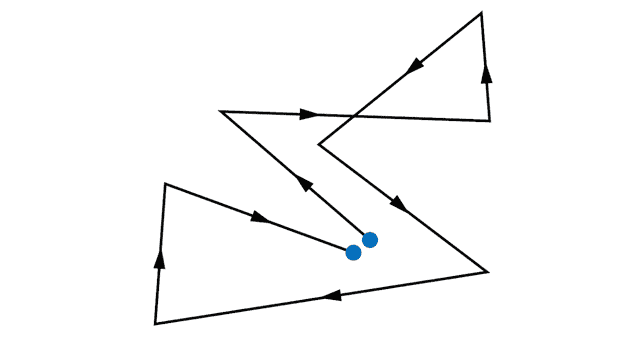 Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E – сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с иономкристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию.
Однако замедленный электрон не остается в состоянии покоя – он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д.
Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).
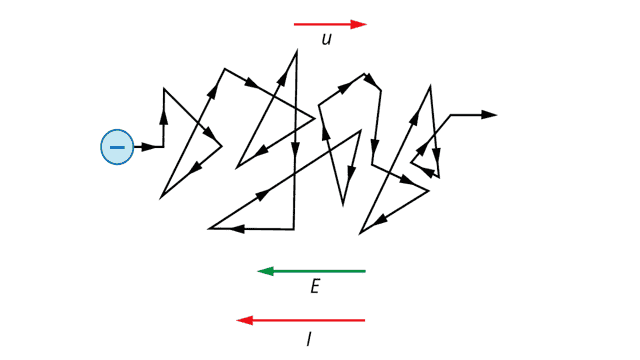 Рис. 2. Дрейф электрона под действием внешнего электрического поля
Рис. 2. Дрейф электрона под действием внешнего электрического поля
В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).
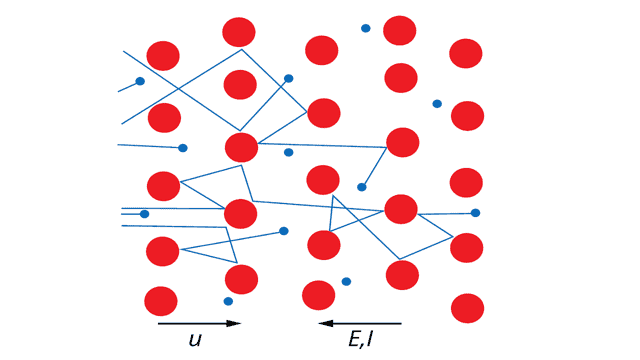 Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ – средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки.
Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10-4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 106 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями.
Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно.
Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток.
Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика – несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это.
Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь.
Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Электрическая проводимость различных веществ. Электронная проводимость металлов — Класс!ная физика
Подробности Просмотров: 634
«Физика — 10 класс»
Как движутся электроны в металлическом проводнике, когда в нём нет электрического поля? Как изменяется движение электронов, когда к металлическому проводнику прикладывают напряжение?
Электрический ток проводят твёрдые, жидкие и газообразные тела. Чем эти проводники отличаются друг от друга?
Вы познакомились с электрическим током в металлических проводниках и с установленной экспериментально вольт-амперной характеристикой этих проводников — законом Ома.
Наряду с металлами хорошими проводниками, т. е. веществами с большим количеством свободных заряженных частиц, являются водные растворы или расплавы электролитов и ионизованный газ — плазма. Эти проводники широко используются в технике.
В вакуумных электронных приборах электрический ток образуют потоки электронов.
Металлические проводники находят самое широкое применение в передаче электроэнергии от источников тока к потребителям. Кроме того, эти проводники используются в электродвигателях и генераторах, электронагревательных приборах и т. д.
Кроме проводников и диэлектриков (веществ со сравнительно небольшим количеством свободных заряженных частиц), имеется группа веществ, проводимость которых занимает промежуточное положение между проводниками и диэлектриками. Эти вещества не настолько хорошо проводят электричество, чтобы их назвать проводниками, но и не настолько плохо, чтобы их отнести к диэлектрикам. Поэтому они получили название полупроводников.
Долгое время полупроводники не играли заметной практической роли. В электротехнике и радиотехнике применяли исключительно различные проводники и диэлектрики. Положение существенно изменилось, когда сначала была предсказана теоретически, а затем обнаружена и изучена легкоосуществимая возможность управления электрической проводимостью полупроводников.
Нет универсального носителя тока. В таблице приведены носители тока в различных средах.

Электронная проводимость металлов.
Начнём с металлических проводников. Вольт-амперная характеристика этих проводников нам известна, но пока ничего не говорилось о её объяснении с точки зрения молекулярнокинетической теории.
Носителями свободных зарядов в металлах являются электроны. Их концентрация велика — порядка 10 28 1/м 3 .
Эти электроны участвуют в беспорядочном тепловом движении. Под действием электрического поля они начинают перемещаться упорядоченно со средней скоростью порядка 10-4 м/с.
Экспериментальное доказательство существования свободных электронов в металлах.
Экспериментальное доказательство того, что проводимость металлов обусловлена движением свободных электронов, было дано в опытах Мандельштама и Папалекси (1913), Стюарта и Толмена (1916). Схема этих опытов такова.
На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга (рис. 16.1). К концам дисков при помощи скользящих контактов подключают гальванометр.
Катушку приводят в быстрое вращение, а затем резко останавливают.
После резкой остановки катушки свободные заряженные частицы некоторое время движутся относительно проводника по инерции, и, следовательно, в катушке возникает электрический ток.
Ток существует незначительное время, так как из-за сопротивления проводника заряженные частицы тормозятся и упорядоченное движение частиц, образующее ток, прекращается.
Направление тока в этом опыте говорит о том, что он создаётся движением отрицательно заряженных частиц. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе, т. е. |q|/m.
Поэтому, измеряя заряд, проходящий через гальванометр за время существования тока в цепи, удалось определить это отношение. Оно оказалось равным 1,8 • 1011 Кл/кг.
Эта величина совпадала с отношением заряда электрона к его массе е/m, найденным ранее из других опытов.
Движение электронов в металле.
Свободные электроны в металле движутся хаотично. При подключении проводника к источнику тока в нём создаётся электрическое поле, и на электроны начинает действовать кулоновская сила = qe. Под действием этой силы электроны начинают двигаться направленно, т. е. на хаотичное движение электронов накладывается Скорость направленного движения увеличивается в течение некоторого времени t0 до тех пор, пока не произойдёт столкновение электронов с ионами кристаллической решётки. При этом электроны теряют направление движения, а затем опять начинают двигаться направленно. Таким образом, скорость направленного движения электрона изменяется от нуля до некоторого максимального значения, равного В результате средняя скорость упорядоченного движения электронов оказывается равной т. е. пропорциональной напряжённости электрического поля в проводнике: υ ~ Е и, следовательно, разности потенциалов на концах проводника, так как где l — длина проводника.
Сила тока в проводнике пропорциональна скорости упорядоченного движения частиц (см. формулу (15.2)). Поэтому можем сказать, что сила тока пропорциональна разности потенциалов на концах проводника: I ~ U.
В этом состоит качественное объяснение закона Ома на основе электронной теории проводимости металлов.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Электрический ток в различных средах — Физика, учебник для 10 класса — Класс!ная физика
Электрическая проводимость различных веществ. Электронная проводимость металлов — Зависимость сопротивления проводника от температуры. Сверхпроводимость — Электрический ток в полупроводниках.
Собственная и примесная проводимости — Электрический ток через контакт полупроводников с разным типом проводимости. Транзисторы — Электрический ток в вакууме. Электронно-лучевая трубка — Электрический ток в жидкостях. Закон электролиза — Электрический ток в газах.
Несамостоятельный и самостоятельный разряды — Плазма — Примеры решения задач по теме «Электрический ток в различных средах»
Классическая электронная теория проводимости Друде-Лоренца
Теория Друде была разработана в 1900 году, через три года после открытия электрона. Затем теория была доработана Лоренцом, и сейчас она является классической и актуальной теорией проводимости металлов.
Электронная теория Друде-Лоренца
Согласно теории, носителями тока в металлах являются свободные электроны.
Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют «электронный газ».
Двигаясь в металле, электроны соударяются между собой и с кристаллической решеткой (это и есть проявление электрического сопротивления проводника). Между соударениями электроны, по аналогии с длиной свободного пробега молекул идеального газа, успевают преодолеть средний путь λ.
Без действия электрического поля, ускоряющего электроны, кристаллическая решетка и электронный газ стремятся к состоянию теплового равновесия.
Приведем основные положения теории Друде:
- Взаимодействие электрона с другими электронами и ионами не учитывается между столкновениями.
- Столкновения являются мгновенными событиями, внезапно меняющими скорость электрона.
- Вероятность для электрона испытать столкновение за единицу времени равна 1τ.
- Состояние термодинамического равновесия достигается благодаря столкновениям.
Важно.
Несмотря на множество допущений, теория Друде-Лорецна хорошо объясняет эффект Холла, явление удельной проводимости и теплопроводность металлов. Именно поэтому она актуальна по сей день, хотя ответы на многие вопросы (например, почему в металле существуют свободные ионы и электроны) смогла дать только квантовая теория твердого тела.
В рамках теории Друде объясняется сопротивление металлов. Оно обусловлено соударениями электронов с узлами кристаллической решетки.
- Выделение тепла, согласно закону Джоуля-Ленца, также происходит по причине соударения электронов с ионами решетки.
- Теплопередача в металлах также осуществляется электронами, а не кристаллической решеткой.
- Терия Друде не объясняет многих явлений, как например сверхпроводимость, и не применима в сильных магнитных полях, в слабых магнитных полях может терять применимость из-за квантовых явлений.
- Среднюю скорость электронов можно вычислить по формуле для идеального газа:
- v=8kTπm
- Здесь k — постоянная Больцмана, T — температура металла, m — масса электрона.
- При включении внешнего электрического поля, на хаотичное движение частиц «электронного газа» накладывается упорядоченное движение электронов под действием сил поля, когда электроны начинают упорядоченно двигаться со средней скоростью u. Величину этой скорости можно оценить из соотношения:
- j=nqu,
- где j — плотность тока, n — концентрация свободных электронов, q — заряд электрона.
- При больших плотностях тока рассчеты дают следующий результат: средняя скорость хаотичного движения электронов во много раз (≈108) больше скорости упорядоченного движения под действием поля. При вычислении суммарной скорости полагают, что
- u→+v→≈v→
Формула Друде
- Формула Друде выводится из кинетического уравнения Больцмана и имеет вид:
- σ=nq2τm*
- Здесь m* — эффективная масса электрона, τ — время релаксации, то есть время, за которое электрон «забывает» о том, в какую сторону двигался после соударения.
- Друде вывел закон Ома для токов в металле:
- j=σ·E→
Опыт Толмена и Стюарта
В 1916 году опыт Толмена и Стюарта дал прямое доказательство тому, что носителями тока в металлах являются электроны.
Суть опыта была в следующем.
Опыт Толмена и Стюарта
Проводящая катушка с проводом длиной L вращалась вокруг своей оси с большой скоростью, а ее концы были замкнуты на гальванометр. Когда катушку резко тормозили, свободные электроны в металле продолжали двигаться по инерции, и гальванометр регистрировал импульс тока.
Считая, что свободные электроны подчиняются законам механики Ньютона, можно записать, что при остановке проводника электрон приобретает ускорение v' (в катушке направлено вдоль проводов). При этом на электрон действует сила, направленная противоположно ускорению.
- F=-mv'
- Под воздействием этой силы электрон ведет себя так, как если бы на него действовало поле E=-mv'q. Эдс, возникающую в катушке при торможении можно записать, как:
- ε=∫LEdl=-mv'q∫Ldl=-mv'qL
- Считая, что ускорение одинаково в каждом витке, можно записать закон Ома для катушки, а затем вычислить заряд, проходящий в ней за время dt:
- IR=-mv'qL
- dq=Idt=-mLdvqRdtdt=-mLdvqR
- Заряд, прошедший от момента начала торможения до остановки:
- q=-mLqR∫v00dv=-mLv0qR
- Опыт Толмена и Стюарта получил хорошее согласование с теорией, полученное экспериментально отношение qmсоответствовало отношению заряда электрона к его массе.
Пример
- При T=300К вычислите среднюю скорость теплового движения свободных электронов.
- Решение.
- Вычислим среднюю скорость, применяя формулу для идеального газа:
- v=8kTπm
- k=1,38·10-23 ДжК
- m=9,31·10-31кг
- Подставляем значения и вычисляем:
- v=8·1,38·10-23·3·1023,14·9,31·10-31≈105 мс






